Тригонометрический круг. Понятие синуса и косинуса числа
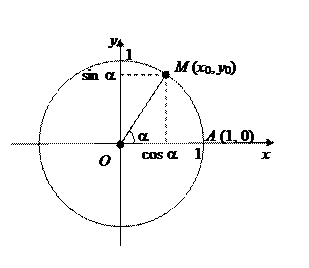 На координатной плоскости построим окружность единичного радиуса с центром в точке О (0,0). Такую окружность будем называть единичной.
На координатной плоскости построим окружность единичного радиуса с центром в точке О (0,0). Такую окружность будем называть единичной.
Для произвольно взятого действительного числа a построим угол, радианная мера которого равна a. Для этого от точки А (1,0) по окружности отложим дугу АМ, длина которой равна |a| единиц. Если 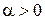 , то откладывать будем против часовой стрелки; если
, то откладывать будем против часовой стрелки; если 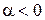 – то по часовой стрелке. Центральный угол
– то по часовой стрелке. Центральный угол 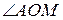 , опирающийся на дугу АМ, имеет величину a.
, опирающийся на дугу АМ, имеет величину a.
Координаты х 0 и у 0 точки М на единичной окружности называются соответственно косинусом и синусом числа a.
С помощью тригонометрического круга доказываются формулы приведения, другие тригонометрические тождества. Так, например, основное тригонометрическое тожество 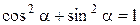 немедленно следует из определений синуса, косинуса и уравнения окружности:
немедленно следует из определений синуса, косинуса и уравнения окружности: 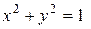 .
.
§ 20. Функция  и ее свойства
и ее свойства
Определение. Функция, которая каждому действительному числу ставит в соответствие его синус, называется синусом и обозначается 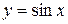 .
.
1.Область определения. Df= R, поскольку значение 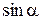 определено для любого действительного числа a.
определено для любого действительного числа a.
2. Множество значений. Поскольку ординаты точек единичной окружности по модулю не превосходят единицы, то 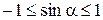 для любого
для любого 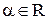 . С другой стороны, любая горизонтальная прямая
. С другой стороны, любая горизонтальная прямая 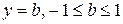 , пересекает единичную окружность хотя бы в одной точке, поэтому любое число b Î[–1, 1]является значением синуса некоторого угла. Следовательно,
, пересекает единичную окружность хотя бы в одной точке, поэтому любое число b Î[–1, 1]является значением синуса некоторого угла. Следовательно, 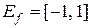 .
.
|
|
|
Периодичность.
Предложение. Функция  является периодической с основным периодом
является периодической с основным периодом  .
.
Доказательство. Поскольку длина единичной окружности равна 2p, то числам a и a+2p соответствует одна и та же точка М на единичной окружности. Поэтому 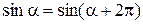 и число 2p является периодом функции
и число 2p является периодом функции  . Докажем, что это основной период, т. е. никакое положительное число меньшее 2p периодом функции синус не является. Пусть
. Докажем, что это основной период, т. е. никакое положительное число меньшее 2p периодом функции синус не является. Пусть 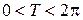 . Сравним значения функции синус в точках
. Сравним значения функции синус в точках 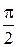 и
и  . Углу
. Углу 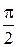 соответствует точка (0,1) на единичной окружности, т.е.
соответствует точка (0,1) на единичной окружности, т.е. 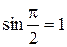 . Так как Т меньше длины единичной окружности, то углу
. Так как Т меньше длины единичной окружности, то углу  соответствует точка единичной окружности, расположенная ниже точки (0,1). Значит,
соответствует точка единичной окружности, расположенная ниже точки (0,1). Значит, 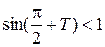 . Таким образом,
. Таким образом, 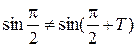 . Это показывает, что число Т,
. Это показывает, что число Т, 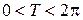 , не является периодом функции
, не является периодом функции  .
.
Предложение доказано.
4.Нули функции, промежутки знакопостоянства. Рассмотрим уравнение 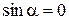 . Прямая у= 0 пересекает единичную окружность в точках (–1,0) и (1,0), которым соответствуют углы 0 и p. Учитывая периодичность функции синус, получаем:
. Прямая у= 0 пересекает единичную окружность в точках (–1,0) и (1,0), которым соответствуют углы 0 и p. Учитывая периодичность функции синус, получаем:
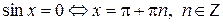 .
.
Поскольку все точки единичной окружности, расположенные в I и II координатных четвертях, имеют положительные ординаты, а точки, расположенные в III и IV четвертях, отрицательные ординаты, то
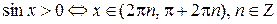 ,
,
 .
.
5.Четность, нечетность.
Предложение. Функция  является нечетной.
является нечетной.
|
|
|
Доказательство. Углам a и –a соответствуют симметричные относительно оси ОХ точки на единичной окружности. Поэтому их ординаты равны по абсолютной величине и противоположны по знаку, т.е. 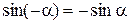 для любого
для любого 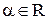 .
.
6.Непрерывность.
Лемма. Неравенство 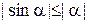 справедливо для любого
справедливо для любого 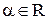 .
.
Доказательство. Заметим, что при 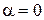 получаем равенство
получаем равенство 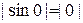 .
.
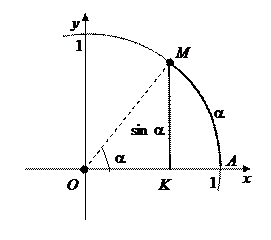 Пусть
Пусть  (см. рис.). Поскольку длина дуги больше длины хорды, на которую она опирается, то и их половины находятся в таком же отношении:
(см. рис.). Поскольку длина дуги больше длины хорды, на которую она опирается, то и их половины находятся в таком же отношении: 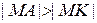 . Так как
. Так как  и
и 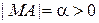 , то
, то  . Если
. Если  , то это неравенство выполняется очевидным образом, поскольку
, то это неравенство выполняется очевидным образом, поскольку 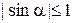 .
.
Пусть 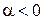 . Тогда
. Тогда 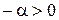 и по доказанному выше
и по доказанному выше 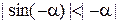 . Воспользовавшись свойством нечетности функции синус, получаем
. Воспользовавшись свойством нечетности функции синус, получаем 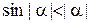 .
.
Таким образом, неравенство 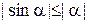 выполняется для любого действительного a.
выполняется для любого действительного a.
Предложение. Функция  непрерывна на R.
непрерывна на R.
Доказательство. Пусть х 0 – произвольная точка числовой прямой. Воспользуемся определением непрерывности функции в точке на языке приращений. Придадим аргументу ненулевое приращение D х. Тогда функция  получит приращение
получит приращение
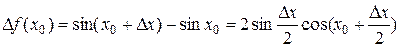 .
.
Пользуясь леммой и ограниченностью косинуса, получаем:
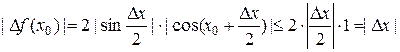 .
.
Из неравенства 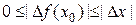 и теоремы о пределе промежуточной функции имеем
и теоремы о пределе промежуточной функции имеем 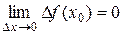 . Следовательно, функция
. Следовательно, функция  непрерывна в точке х 0. Так как х 0 – произвольная точка числовой прямой, то функция непрерывна на R.
непрерывна в точке х 0. Так как х 0 – произвольная точка числовой прямой, то функция непрерывна на R.
|
|
|
Следовательно, f – нечетная функция.
7.Монотонность.
Предложение. Функция 
1) строго возрастает на промежутках 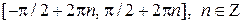 ,
,
2) строго убывает на промежутках 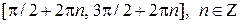 .
.
Доказательство. Опираясь на свойство периодичности синуса, достаточно доказать, что функция  строго возрастает на
строго возрастает на 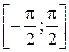 и строго убывает на
и строго убывает на 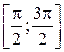 . Докажем ее возрастание на
. Докажем ее возрастание на 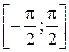 . Возьмем произвольные точки
. Возьмем произвольные точки 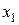 и
и 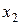 , такие что
, такие что 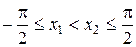 . Покажем, что разность значений функции в этих точках
. Покажем, что разность значений функции в этих точках 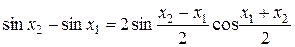 положительна. Из неравенств
положительна. Из неравенств 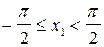 ,
,  и
и 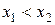 получаем
получаем 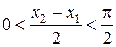 и
и 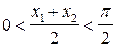 . Полученным значениям аргументов соответствуют точки единичной окружности, расположенные в I координатной четверти. Поэтому
. Полученным значениям аргументов соответствуют точки единичной окружности, расположенные в I координатной четверти. Поэтому 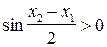 и
и 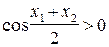 , следовательно,
, следовательно, 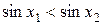 . Тем самым доказано, что функция
. Тем самым доказано, что функция  строго возрастает на
строго возрастает на 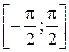 .
.
Докажем, что функция убывает на отрезке 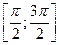 . Для произвольных точек
. Для произвольных точек 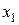 и
и 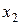 в этом случае из неравенств
в этом случае из неравенств 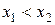 ,
, 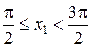 и
и 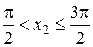 следует
следует  и
и 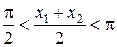 . Тогда
. Тогда 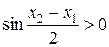 и
и  , следовательно,
, следовательно, 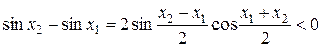 . Получили
. Получили 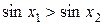 . Тем самым доказано, что функция
. Тем самым доказано, что функция  строго убывает на отрезке
строго убывает на отрезке 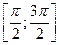 .
.
8. Экстремумы функции  . Так как функция возрастает на промежутке
. Так как функция возрастает на промежутке 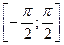 и убывает на промежутках
и убывает на промежутках 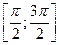 и
и 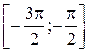 , то
, то 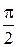 – точка максимума функции синус, а
– точка максимума функции синус, а 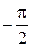 – ее точка минимума. В силу периодичности функции получаем, что точки
– ее точка минимума. В силу периодичности функции получаем, что точки 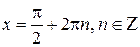 являются точками максимума, а точки
являются точками максимума, а точки 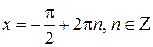 точками минимума функции
точками минимума функции  .
.
|
|
|
9. График функции  называется синусоидой.
называется синусоидой.
 |
§ 21. Функция 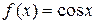 и ее свойства
и ее свойства
Определение. Функция, которая каждому действительному числу ставит в соответствие его косинус, называется косинусом и обозначается 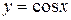 .
.
1.Область определения. Поскольку значение 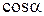 определено для любого действительного числа a, то Df= R.
определено для любого действительного числа a, то Df= R.
2. Множество значений. Так как абсциссы точек единичной окружности по модулю не превосходят единицы, то 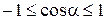 для любого
для любого 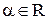 . С другой стороны, любая вертикальная прямая
. С другой стороны, любая вертикальная прямая 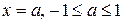 пересекает единичную окружность хотя бы в одной точке, поэтому любое число а Î[–1, 1]является значением косинуса некоторого угла. Следовательно,
пересекает единичную окружность хотя бы в одной точке, поэтому любое число а Î[–1, 1]является значением косинуса некоторого угла. Следовательно, 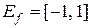 .
.
Периодичность.
Предложение. Функция 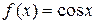 является периодической с основным периодом
является периодической с основным периодом  .
.
Доказательство. Поскольку длина единичной окружности равна 2p, то числам a и a+2p соответствует одна и та же точка М на единичной окружности. Поэтому 2p является периодом функции 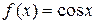 . Докажем, что это основной период, т. е. никакое положительное число меньшее 2p периодом функции косинус не является. Пусть
. Докажем, что это основной период, т. е. никакое положительное число меньшее 2p периодом функции косинус не является. Пусть 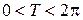 . Сравним значения функции косинус в точках 0 и Т. Углу 0 радиан соответствует точка (1,0) на единичной окружности, т.е.
. Сравним значения функции косинус в точках 0 и Т. Углу 0 радиан соответствует точка (1,0) на единичной окружности, т.е. 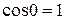 . Так как Т меньше длины единичной окружности, то углу
. Так как Т меньше длины единичной окружности, то углу 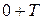 соответствует точка единичной окружности, отличная от (1,0). Значит,
соответствует точка единичной окружности, отличная от (1,0). Значит, 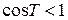 . Таким образом,
. Таким образом, 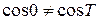 . Это показывает, что никакое число Т,
. Это показывает, что никакое число Т, 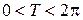 , не является периодом функции косинус.
, не является периодом функции косинус.
Предложение доказано.
4.Нули функции, промежутки знакопостоянства. Рассмотрим уравнение  . Прямая х= 0 пересекает единичную окружность в точках (0, –1) и (0,1), которым соответствуют углы –p/2 и p/2. Учитывая периодичность функции косинус, получаем:
. Прямая х= 0 пересекает единичную окружность в точках (0, –1) и (0,1), которым соответствуют углы –p/2 и p/2. Учитывая периодичность функции косинус, получаем:
 .
.
Поскольку все точки единичной окружности, расположенные в I и IV координатных четвертях, имеют положительные абсциссы, а точки, расположенные в II и III четвертях, – отрицательные абсциссы, то
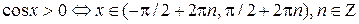 ,
,
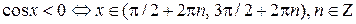 .
.
5.Четность, нечетность.
Предложение. Функция 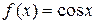 является четной.
является четной.
Доказательство. Углам a и –a соответствуют симметричные относительно оси ОХ точки на единичной окружности. Поэтому их абсциссы равны, т.е. 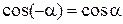 для любого
для любого 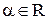 .
.
6.Непрерывность.
Предложение. Функция 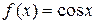 непрерывна на R.
непрерывна на R.
Доказательство. Пусть х 0 – произвольная точка числовой прямой. Воспользуемся определением непрерывности функции в точке на языке приращений. Придадим аргументу ненулевое приращение D х. Тогда функция 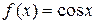 получит приращение
получит приращение
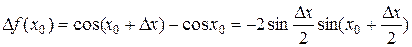 .
.
Пользуясь леммой и ограниченностью синуса, получаем:
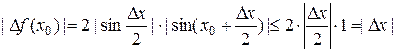 .
.
Из неравенства 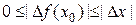 и теоремы о пределе промежуточной функции имеем
и теоремы о пределе промежуточной функции имеем 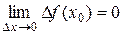 . Следовательно, функция
. Следовательно, функция 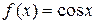 непрерывна в точке х 0. Так как х 0 – произвольная точка числовой прямой, то функция непрерывна на R.
непрерывна в точке х 0. Так как х 0 – произвольная точка числовой прямой, то функция непрерывна на R.
Следовательно, f – нечетная функция.
7.Монотонность.
Предложение. Функция 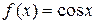
1) строго возрастает на промежутках  ,
,
2) строго убывает на промежутках 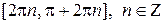 .
.
Доказательство. Опираясь на свойство периодичности, достаточно доказать, что функция 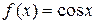 строго возрастает на
строго возрастает на 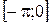 и строго убывает на
и строго убывает на  . Докажем ее возрастание на
. Докажем ее возрастание на 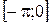 . Возьмем произвольные точки
. Возьмем произвольные точки 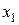 и
и 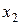 , такие что
, такие что 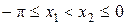 . Покажем, что разность значений функции в этих точках
. Покажем, что разность значений функции в этих точках 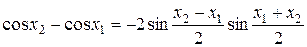 положительна. Из неравенств
положительна. Из неравенств 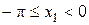 ,
,  и
и 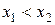 получаем
получаем 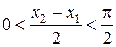 и
и 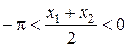 . Для этих значений аргумента
. Для этих значений аргумента 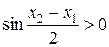 и
и 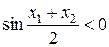 , следовательно,
, следовательно, 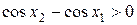 , т.е.
, т.е.  . Тем самым доказано, что функция
. Тем самым доказано, что функция 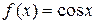 строго возрастает на
строго возрастает на 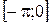 .
.
Докажем, что функция убывает на отрезке  . Для произвольных точек
. Для произвольных точек 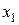 и
и 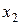 в этом случае из неравенств
в этом случае из неравенств 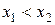 ,
, 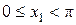 и
и 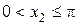 следует
следует  и
и 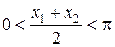 . Тогда
. Тогда 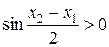 и
и 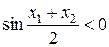 , следовательно,
, следовательно,  . Получили
. Получили 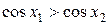 . Тем самым доказано, что функция
. Тем самым доказано, что функция 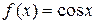 строго убывает на
строго убывает на  .
.
8. Экстремумы функции 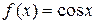 . Так как функция возрастает на промежутках
. Так как функция возрастает на промежутках 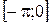 и
и 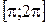 и убывает на промежутке
и убывает на промежутке  , то 0 – точка максимума функции косинус, а p – ее точка минимума. В силу периодичности функции получаем, что точки
, то 0 – точка максимума функции косинус, а p – ее точка минимума. В силу периодичности функции получаем, что точки 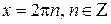 являются точками максимума, а точки
являются точками максимума, а точки 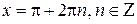 – точками минимума функции
– точками минимума функции 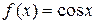 .
.
9. График функции 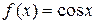 также называется синусоидой.
также называется синусоидой.
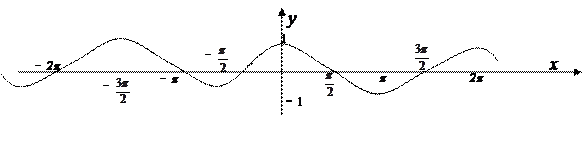
Замечание. Из формул приведения известно, что 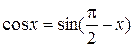 для любого действительного х. Поэтому свойства функции
для любого действительного х. Поэтому свойства функции 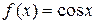 могут бытьполучены как следствия свойств функции синус.
могут бытьполучены как следствия свойств функции синус.
§ 22. Функция 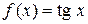 и ее свойства
и ее свойства
Определение. Тангенсом действительного числа  называется число
называется число 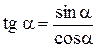 .
.
Функция 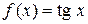 является частным функций
является частным функций 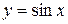 и
и 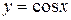 . Поэтому ее свойства вытекают из свойств этих функций.
. Поэтому ее свойства вытекают из свойств этих функций.
1.Область определения. Так как значение 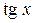 определено для любого числа x, при котором
определено для любого числа x, при котором  , то Df = R\{
, то Df = R\{ 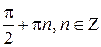 }.
}.
Периодичность.
Предложение. Функция 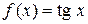 является периодической с основным периодом
является периодической с основным периодом 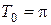 .
.
Доказательство. Так как Df = R\{ 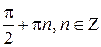 }, то никакое положительное число, меньшее p, периодом функции
}, то никакое положительное число, меньшее p, периодом функции 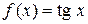 не является.Осталось показать, что p – период:
не является.Осталось показать, что p – период:
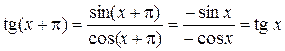 .
.
Предложение доказано.
3.Нули функции, промежутки знакопостоянства.
 .
.
Если 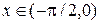 , то
, то 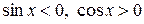 . Следовательно,
. Следовательно, 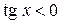 .
.
Если 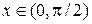 , то
, то 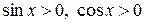 . Следовательно,
. Следовательно, 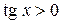 .
.
Учитывая периодичность функции тангенс, получаем:
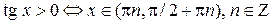 ,
,
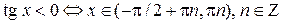 .
.
4.Четность, нечетность.
Предложение. Функция 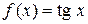 является нечетной.
является нечетной.
Доказательство. Областьопределения функции 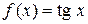 является симметричным относительно нуля множеством и
является симметричным относительно нуля множеством и
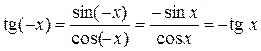 для любого
для любого 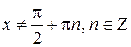 .
.
Следовательно, функция тангенс – нечетная.
5.Монотонность.
Предложение. Функция 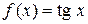 строго возрастает на интервалах
строго возрастает на интервалах 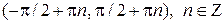 .
.
Доказательство. Опираясь на свойство периодичности, достаточно доказать, что функция 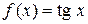 строго возрастает на
строго возрастает на 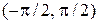 . Возьмем произвольные точки
. Возьмем произвольные точки 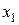 и
и 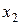 , такие что
, такие что 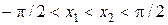 . Рассмотрим разность значений функции в этих точках
. Рассмотрим разность значений функции в этих точках 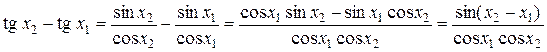 . Поскольку
. Поскольку 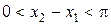 и
и 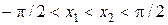 , то
, то 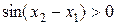 и
и 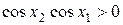 . Следовательно,
. Следовательно, 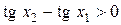 , т.е.
, т.е. 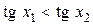 . Тем самым доказано, что функция
. Тем самым доказано, что функция 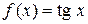 строго возрастает на интервале
строго возрастает на интервале 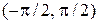 .
.
6.Непрерывность. Функция 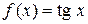 непрерывна на своей области определения как частное непрерывных функций.
непрерывна на своей области определения как частное непрерывных функций.
Асимптоты.
Предложение. Прямые 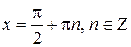 , являются вертикальными асимптотами функции
, являются вертикальными асимптотами функции 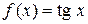 .
.
Доказательство. Найдем односторонние пределы функции 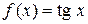 в точке
в точке 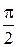 :
:
 ,
, 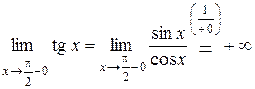 .
.
Из периодичности тангенса следует, что во всех точках 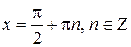 , ееодносторонние пределы равны бесконечности. Предложение доказано.
, ееодносторонние пределы равны бесконечности. Предложение доказано.
8. Множество значений.
Предложение. Множеством значений функции 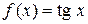 является множество всех действительных чисел.
является множество всех действительных чисел.
Доказательство. Достаточно доказать, что на интервале 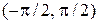 функция тангенс принимает все действительные значения.
функция тангенс принимает все действительные значения.
Пусть r – произвольное действительное число. Так как 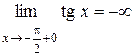 и
и 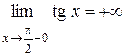 , то существуют точки х 1 и х 2 (х 1 < х 2), для которых
, то существуют точки х 1 и х 2 (х 1 < х 2), для которых 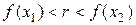 . Из непрерывности функции на R следует, что она непрерывна на отрезке
. Из непрерывности функции на R следует, что она непрерывна на отрезке  . По теореме Больцано-Коши о промежуточных значениях непрерывной на отрезке функции заключаем, что число r является значением функции в некоторой точке отрезка
. По теореме Больцано-Коши о промежуточных значениях непрерывной на отрезке функции заключаем, что число r является значением функции в некоторой точке отрезка  , т. е.
, т. е. 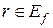 . Следовательно,
. Следовательно, 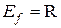 .
.
9. График функции 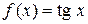 называется тангенсоидой.
называется тангенсоидой.
 |
§ 23. Функция 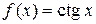 и ее свойства
и ее свойства
Определение. Котангенсом действительного числа 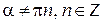 называется число
называется число 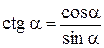 .
.
Функция 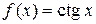 является частным функций
является частным функций 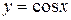 и
и 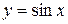 . Поэтому ее свойства следуют из свойств этих функций. Кроме того,
. Поэтому ее свойства следуют из свойств этих функций. Кроме того, 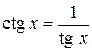 для всех
для всех 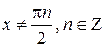
1.Область определения. Так как значение  определено для любого числа x, при котором
определено для любого числа x, при котором 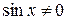 , то Df = R\{
, то Df = R\{ 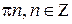 }.
}.
Периодичность.
Предложение. Функция 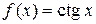 является периодической с основным периодом
является периодической с основным периодом 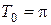 .
.
Доказательство. Так как Df= R\{ 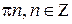 }, то никакое положительное число, меньшее p, периодом функции
}, то никакое положительное число, меньшее p, периодом функции 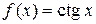 не является.Осталось показать, что число p – период:
не является.Осталось показать, что число p – период:
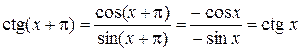 .
.
3.Нули функции, промежутки знакопостоянства.
Найдем нули функции, для этого решим уравнение: 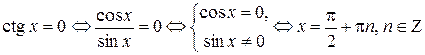 .
.
Из тождества 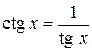 (
(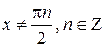 ) следует, что функции тангенс и котангенс при
) следует, что функции тангенс и котангенс при 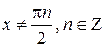 принимают одинаковые по знаку значения. Следовательно,
принимают одинаковые по знаку значения. Следовательно,
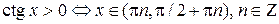 ,
,
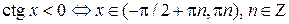 .
.
4.Четность, нечетность.
Предложение. Функция 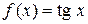 является нечетной.
является нечетной.
Доказательство. Область определения функции 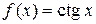 является симметричным относительно нуля множеством и
является симметричным относительно нуля множеством и
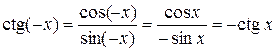 для любого
для любого 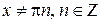 .
.
Следовательно, функция котангенс – нечетная.
5.Монотонность.
Предложение. Функция 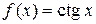 строго убывает на интервалах
строго убывает на интервалах 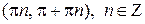 .
.
Доказательство. Опираясь на свойство периодичности, достаточно доказать, что функция 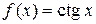 строго убывает на
строго убывает на 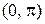 . Возьмем произвольные точки
. Возьмем произвольные точки 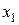 и
и 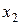 , такие что
, такие что  . Рассмотрим разность значений функции в этих точках
. Рассмотрим разность значений функции в этих точках 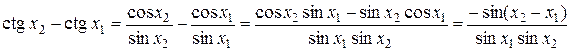 . Поскольку
. Поскольку 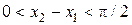 и
и  , то
, то 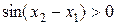 и
и 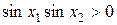 . Следовательно,
. Следовательно, 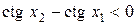 , т.е.
, т.е. 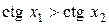 . Тем самым доказано, что функция
. Тем самым доказано, что функция 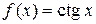 строго убывает на
строго убывает на 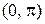 .
.
6.Непрерывность. Функция 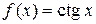 непрерывна на своей области определения как частное непрерывных функций.
непрерывна на своей области определения как частное непрерывных функций.
Асимптоты.
Предложение. Прямые 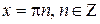 являются вертикальными асимптотами функции
являются вертикальными асимптотами функции 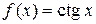 .
.
Доказательство. Найдем односторонние пределы функции 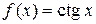 в точке 0:
в точке 0:
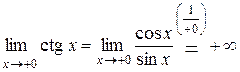 ,
, 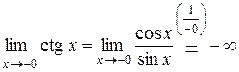 .
.
В силу периодичности функции тангенс заключаем, что в точках 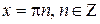 , ееодносторонние пределы равны бесконечности. Предложение доказано.
, ееодносторонние пределы равны бесконечности. Предложение доказано.
8. Множество значений.
Предложение. Множеством значений функции 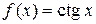 является множество всех действительных чисел.
является множество всех действительных чисел.
Доказательство. Число 0 является значением функции котангенс, так как 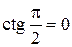 . Докажем, что все числа, не равные нулю, также являются значениями функции
. Докажем, что все числа, не равные нулю, также являются значениями функции 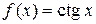 .
.
Возьмем произвольное действительное число 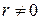 . Так как множеством значений тангенса является множество всех действительных чисел и
. Так как множеством значений тангенса является множество всех действительных чисел и 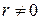 , то существует точка х 0, для которой
, то существует точка х 0, для которой 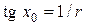 . Тогда
. Тогда 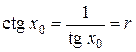 , т. е.
, т. е. 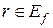 . Следовательно,
. Следовательно, 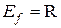 .
.
9. График функции 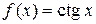 .
.
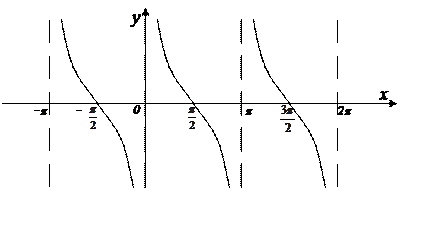
Дата добавления: 2015-12-17; просмотров: 22; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
