Нули и промежутки знакопостоянства.
Так как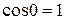 
, то 
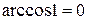. Функция 
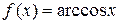строго убывает, поэтому 
при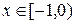 
.
7. График функции .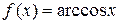
Графики функци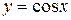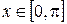й 
, 
, и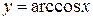 
симметричны относительно прямой 
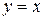, как графики взаимно-обратных функций.
§ 26. Функция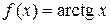 
и ее свойства
Функция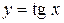 
строго возрастает на интервале 
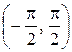, поэтому ее сужение на этот интервал является обратимой функцией.
Определение. Функция, обратная для сужения функции 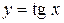на интервал 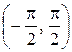, называется арктангенсом и обозначается .
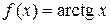Из определения обратной функции следует:
.
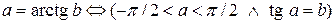1. Область определения, множество значений. Из определения обратной функции следует, что областью определения и множеством значений функции 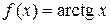является соответственно множество значений и область определения функции 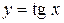, где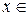 
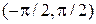. Таким образом, 
, 
.
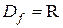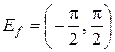2. Ограниченность. Функция 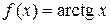ограничена, так как ее множество значений 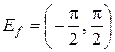является ограниченным числовым множеством. Таким образом, 
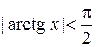для любого действительного х.
3. Непрерывность. Функция 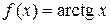непрерывна как обратная для непрерывной функции.
4. Четность, нечетность.
Предложение. Функция 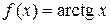является нечетной.
Доказательство. Область определения арктангенса 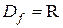– симметричное относительно нуля множество.
Проверим выполнимость равенства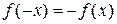 
. Возьмем произвольную точку 
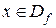и докажем равенство 
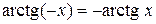. Пусть 
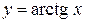. По определению арктангенса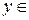 
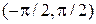и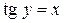 
. Тогда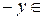 
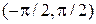и в силу нечетности тангенса 
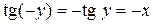. По определению арктангенса имеем: 
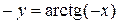. Из равенств 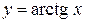и 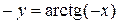получаем .
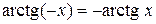5. Монотонность. Функция 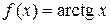является обратной для строго возрастающей функции, следовательно, также строго возрастает на своей области определения.
Дата добавления: 2015-12-17; просмотров: 13; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!