IV. Ограниченность.
Определение. Функция f называется ограниченной сверху на множестве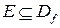 
, если существует такое число М, что 
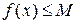для всех х из множества Е:
f ограничена сверху на множестве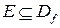 
.
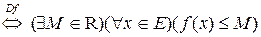Определение. Функция f называется ограниченной снизу на множестве 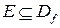, если существует такое число т, что 
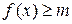для всех х из множества Е:
f ограничена снизу на множестве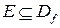 
.
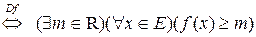Определение*. Функция f называется ограниченной на множестве 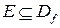, если она ограничена сверху и снизу на этом множестве, т.е. существуют такие числа т и М, что 
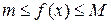для всех х из
множества Е:
Часто при исследовании на ограниченность оказывается удобно использовать следующее определение ограниченной.
Определение**. Функция f называется ограниченной на множестве 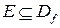, если существует такое число М > 0, что 
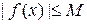для всех х из множества Е:
f ограничена на множестве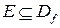 
.
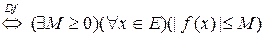Предложение. Определения* и ** ограниченной на множестве функции эквивалентны.
Доказательство. 1. Пусть функция f ограничена на множестве 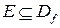по определению *, т.е. существуют такие числа т и М, что 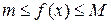для всех элементов х из множества Е Пусть М 0 = max{| т |, | М |}. Очевидно, М 0³0. По свойствам модуля действительного числа для всех элементов х из множества Е выполняется:
– М 0= – max{| т |, | М |}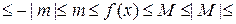 
max{| т |, | М |}= М 0
Таким образом, – М 0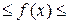 
М 0 Û 
М 0 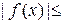для всех х из множества Е. Следовательно, функция f ограничена на множестве E Í Df по определению *.
2. Пусть функция f ограничена на множестве E Í Df по определению **, т.е. найдется такое неотрицательное число М 0, что для всех х из множества Е выполняется неравенство 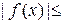М 0 Û – М 0 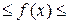М 0. Обозначив М= М 0 и т= – М 0, получаем, что функция f ограничена на множестве E Í Df по определению *.
Определение. Функция f называется ограниченной (сверху, снизу), если она ограничена (сверху, снизу) на своей области определения.
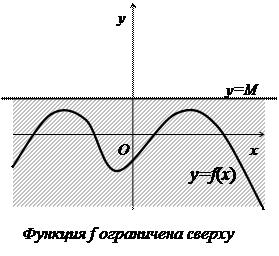
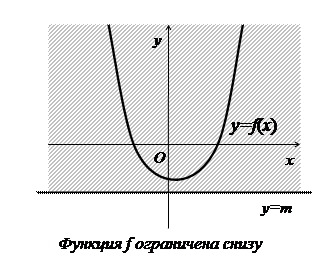
С геометрической точки зрения ограниченность функции сверху (снизу) означает, что существует такая горизонтальная прямая у = М (у = т), выше (ниже) которой точек графика функции нет. График ограниченной функции содержится в некоторой горизонтальной полосе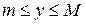 
. Заметим, что указанные в определениях числа т и М определяются не единственным образом. При условии их существования можно указать бесконечно много значений т и М.
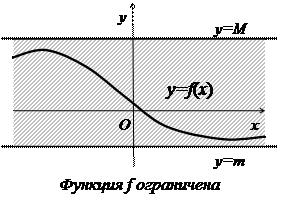
Примеры. Исследуем на ограниченность следующие функции.
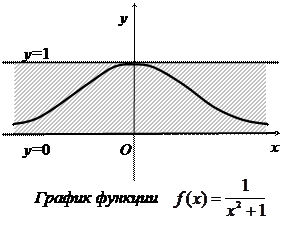
1. 
.
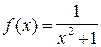R. Для любого действительного числа х справедливо:
1) 
;
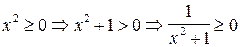2) 
.
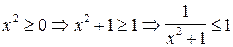Таким образом, нашлись такие значения т= 0 и М= 1, что для всех х выполняется неравенство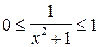 
.
Вывод: функция f является ограниченной.
2. 
.
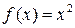1) Функция 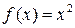ограничена снизу, так как для любого х выполняется неравенство 
.
2) Докажем, что данная функция не ограничена сверху.
Нужно показать следующее: каково бы ни было действительное число М, для него найдется точка х 0, в которой значение функции больше, чем М. Рассмотрим случаи М < 0 и М ³ 0.
Если М < 0, то в качестве х 0 можно взять любое число, тогда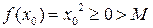 
.
Если М ³ 0, то возьмем 
. Тогда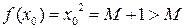 
.
Следовательно, функция 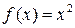не ограничена сверху.
Вывод. Данная функция ограничена снизу, не ограничена сверху, не ограничена.
Дата добавления: 2015-12-17; просмотров: 15; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!