Операции над функциями
Определение. Суммой функций f и g называется функция f + g, область определения и закон соответствия которой определяются следующим образом:
1) 
;
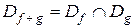2) 
для всех 
.
Определение. Произведением функций f и g называется функция fg, для которой:
1) 
;
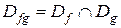2) 
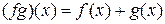для всех 
.
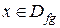Определение. Частным функций f и g называется функция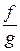 
, для которой:
1) 
;
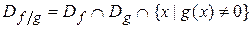2) 
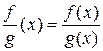для всех 
.
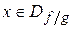Пример. Найдемобласть определения функции 
.
Данная функция является частным функци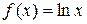й 
и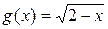 
. По определению частного двух функций ее область определения состоит из тех значений х, для которых выполнены три условия: 
, 
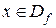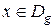и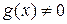 
. Получаем систему:
.
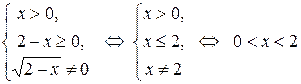Таким образом, областью определения данной функции является множество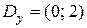 
.
Определение. Композицией функций f и g называется функция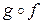 
, для которой:
1) 
;
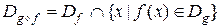2) 
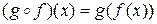для всех 
.
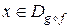Пример. Для функци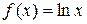й и 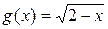найдем композици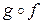и и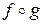 
и их области определения.
1. По определению композиции функций f и g область определения функции 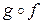состоит из тех значений х, для которых выполнены два условия: 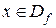и 
. Получаем систему:
.
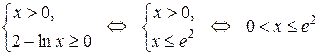Таким образом, областью определения композиции 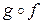является множество 
.
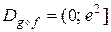Значения функции 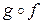во всех точках множества 
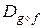находятся по формуле: 
.
2. Для функции 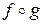область определения находим, исходя из услови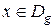й и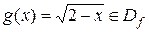 
. Получаем систему:
.
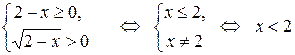Получили: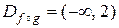 
. Во всех точках области определения значения функции 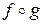вычисляются по формуле: 
.
Заметим, что функци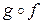и и 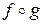не равны. Это следует хотя бы из того, что полученные функции имеют разные области определения.
|
|
|
Вывод. Операция композиции функций не коммутативна.
Определение. Сужением функций f на множество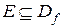 
называется функция 
, для которой:
1) 
;
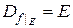2) 
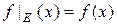для всех 
.
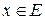Пример. Рассмотрим функции f и g, заданные одной формулой, но на разных множествах:
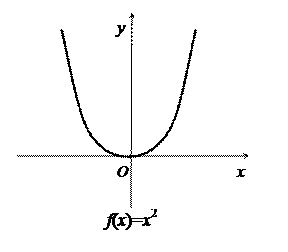
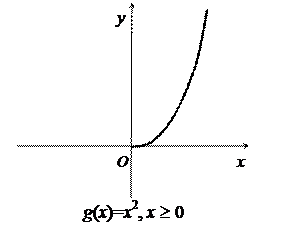
Функция g является сужением функции f на множество [0,+¥): g = f |[0,+¥).
Определение. Пусть функция f инъективна. Обратной функцией для функции f называется функция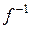 
, область определения и закон соответствия которой определяются следующим образом:
1) 
;
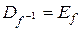2) 
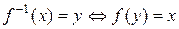для всех 
.
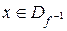Определение. Функция называется обратимой, если она имеет обратную функцию.
Очевидно, функция обратима в том и только в том случае, когда она каждое свое значение принимает ровно один раз.
Замечание. Так как точки (х, у) и (у, х) симметричны относительно прямой у=х, то графики числовых функций f и 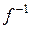симметричны относительно биссектрисы I и III координатных углов.
Пример. Рассмотрим функцию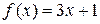 
. Каждое свое значение она принимает ровно один раз, следовательно, обратима. Найдем обратную для нее функцию 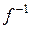. Для этого из равенства 
выразим переменную х. Получим: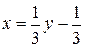 
. Таким образом, обратная функция каждому значению y ставит в соответствие число 
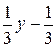. Переобозначив переменную, получаем: 
.
|
|
|
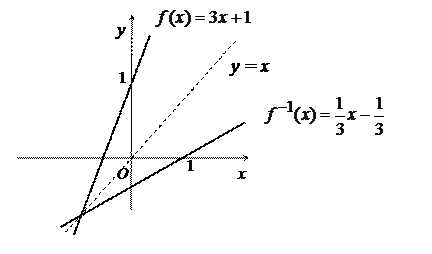
§5. Свойства функций: монотонность, четность, нечетность, периодичность, ограниченность
I. Монотонность.
Определение. Функция f называется строго возрастающей [1] на множестве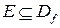 
, если для любых точек х 1 и х 2 из множества E, удовлетворяющих неравенству х 1 < х 2, выполняется 
:
.
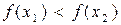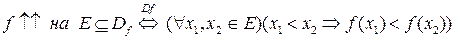Определение. Функция f называется возрастающей [2] на множестве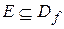 
, если:
Аналогично определяется строгое убывание и убывание функции на множестве[3]:
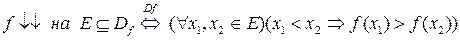
Определение. Функция называется монотонной (строго монотонной) на множестве 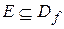, если она возрастает или убывает (строго возрастает или строго убывает) на этом множестве.
Определение. Функция называется постоянной на множестве
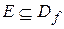, если все ее значения на этом множестве равны между собой:
.
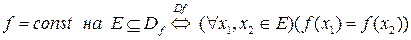Очевидно, функция постоянна на множестве тогда и только тогда, когда она возрастает и убывает на этом множестве.
Определение. Функция называется монотонной (строго монотонной, постоянной), если она монотонна (строго монотонна, постоянна) на своей области определения.
Геометрически строгое возрастание функции означает, что при движении слева направо по графику функции движение происходит вверх («в горку»), а строгое убывание – это движение вниз («с горки»).
|
|
|
Пример. Рассмотрим свойства, связанные с монотонностью, для функции y = f (х), заданной графически:
Функция y = f (х):
- возрастает на промежутках: (-¥, x 4]; [ x 5, x 6]; [ x 6, +¥);
- строго возрастает на промежутках: [ x 1, x 2]; [ x 3, 0]; [ x 5, x 6];
- убывает на промежутках: [0, x 5]; [ x 6, +¥);
- строго убывает на промежутках: [ x 4, x 5]; [ x 6, +¥);
- постоянна на промежутках: [ x 2, x 3]; [0, x 4];
- не монотонна.
Пример. Докажем по определению, что функция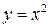 
строго возрастает на множестве 
.
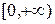Пусть х 1 и х 2 - произвольные точки из 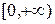, удовлетворяющие неравенству х 1 < х 2 . Сравним значения функции в этих точках. Для этого оценим знак разности 
.
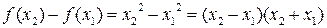Так как х 1 < х 2, то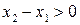 
, а из неравенств 
и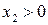 
следует, что 
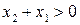. Таким образом, оба сомножителя положительны и, значит, 
. Доказательство завершено.
Замечание. Из возрастания (или убывания) функции на отдельных множествах не следует ее возрастание (убывание) на объединении этих множеств.
Пример. Функция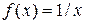 
убывает на интервалах(-¥,0) и (0,+¥), но не является убывающей на множестве (-¥,0)È(0,+¥).
Действительно, легко показать, что функция убывает на каждом из интервалов (-¥,0) и (0,+¥) (сделайте это самостоятельно).
При этом для точек -1 и 1 из множества (-¥,0)È(0,+¥) выполнено -1<1 и в то же время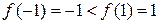 
, т.е. большему значению аргумента соответствует большее значение функции. Это и означает, что данная функция не является убывающей на множестве (-¥,0)È(0,+¥).
|
|
|
Дата добавления: 2015-12-17; просмотров: 19; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!