Множество значений.
Предложение. 
Доказательство. 1.Пусть п четно. Тогда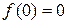 
, 
для всех 
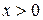и, так как функция f при четном п является четной, то для всех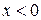 
.
Осталось доказать, что любое число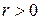 
является значением функции f. Пусть 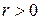– произвольное действительное число. Поскольку 
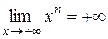(см. п. 6), то существует такая точка а > 0 на числовой прямой, что 
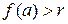. Из непрерывности функции f на R следует ее непрерывность на отрезке 
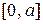. Так как 
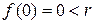и 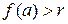, то по теореме Вейерштрасса о промежуточных значениях непрерывной на отрезке функции заключаем, что число r является значением функции f в некоторой точке отрезка .
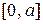Таким образом, доказали, что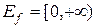 
, если п четно.
2. Пусть п нечетно и r – произвольное действительное число. Так как 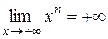и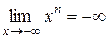 
, то существуют точки х 1 и х 2 (х 1 < х 2), для которых 
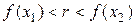. Из непрерывности функции на R следует, что она непрерывна на отрезке 
. По теореме Больцано-Коши о промежуточных значениях непрерывной на отрезке функции заключаем, что число r является значением функции в некоторой точке отрезка , т. е.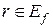 
. Следовательно, 
.
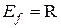Ограниченность.
Так как множество значений функции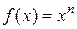 
(
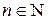) является неограниченным сверху числовым множеством, то функция f неограниченна сверху при любом п, и, следовательно, неограниченна. Кроме того, 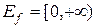, если п четно, – ограниченное снизу множество и 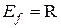, если п нечетно, – неограниченное снизу множество. Таким образом, функция f ограничена снизу при четном п и не ограничена снизу при нечетном п.
|
|
|
10. График функции. Из доказанных в п. 7 неравенств следует, что при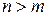 
график функции 
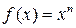на интервале 
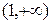расположен выше графика функции 
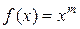и ниже на интервале 
.
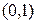График степенной функции 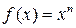при п= 2 называется параболой, при п= 3 – кубической параболой.
 | |||
 |
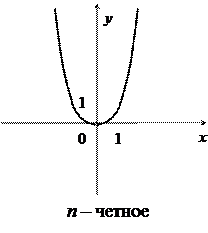Дата добавления: 2015-12-17; просмотров: 18; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!