Численное интегрирование
Задача численного интегрирования заключается в вычислении значения определенного интеграла I на основании ряда значений подынтегральной функции в точках промежутка интегрирования. Формулы численного интегрирования называются квадратурными формулами. Рассмотрим простейшие из них, использующие локальную интерполяцию при точечной аппроксимации подынтегральной функции.
С помощью точек  разобьем отрезок интегрирования
разобьем отрезок интегрирования 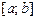 на n равных частичных отрезков
на n равных частичных отрезков 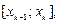
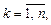 с шагом интегрирования
с шагом интегрирования 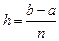 и обозначим
и обозначим 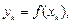
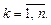 Величина
Величина 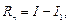 где
где 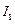 – численное значение выбранной квадратурной формулы, называется остаточным членом квадратурной формулы.
– численное значение выбранной квадратурной формулы, называется остаточным членом квадратурной формулы.
Формула левых прямоугольников:
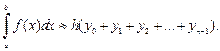
Формула правых прямоугольников:
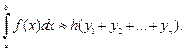
Если 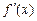 непрерывна на
непрерывна на 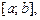 то для формул левых и правых прямоугольников выполняется
то для формул левых и правых прямоугольников выполняется
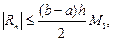
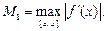
Формула средних прямоугольников:
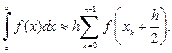 (33.21)
(33.21)
Если 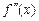 непрерывна на
непрерывна на 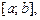 то для формулы средних прямоугольников выполняется
то для формулы средних прямоугольников выполняется
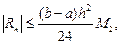
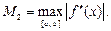 (33.22)
(33.22)
Формула трапеций:
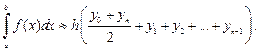 (33.23)
(33.23)
Если 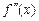 непрерывна на
непрерывна на 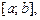 то для формулы трапеций выполняется
то для формулы трапеций выполняется
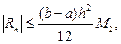
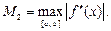 (33.24)
(33.24)
Формула Симпсона (формула парабол):
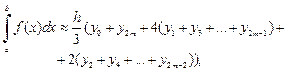 (33.25)
(33.25)
где 
Если 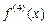 непрерывна на
непрерывна на 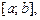 то для формулы Симпсона выполняется
то для формулы Симпсона выполняется
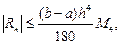
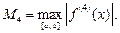 (33.26)
(33.26)
Пример 1. Вычислить интеграл 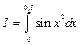 с точностью до
с точностью до 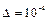 путем разложения подынтегральной функции в степенной ряд.
путем разложения подынтегральной функции в степенной ряд.
Решение. Воспользуемся формулой Маклорена
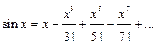
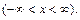
Заменяя в ней x на  получим ряд
получим ряд
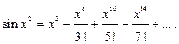
Этот ряд сходится при любом 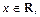 поэтому его можно почленно интегрировать. Тогда
поэтому его можно почленно интегрировать. Тогда
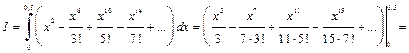
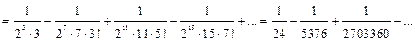 Полученный числовой ряд является знакочередующимся. Так как
Полученный числовой ряд является знакочередующимся. Так как
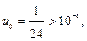
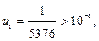 но
но 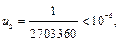 то отсюда имеем оценку остаточного члена:
то отсюда имеем оценку остаточного члена:
|
|
|
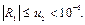
Поэтому для обеспечения заданной степени точности достаточно взять два члена ряда
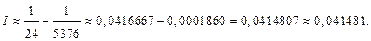
Следовательно, 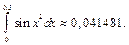
Пример 2. Вычислить интеграл 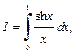 разлагая подынтегральную функцию в степенной ряд и используя три члена этого разложения. Определить абсолютную погрешность результата.
разлагая подынтегральную функцию в степенной ряд и используя три члена этого разложения. Определить абсолютную погрешность результата.
Решение. Воспользуемся формулой

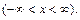
Получим
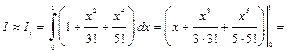
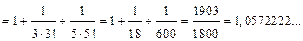
Найдем абсолютную погрешность
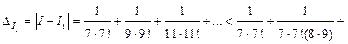
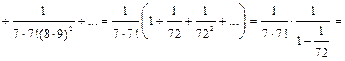
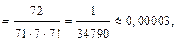
т. е. 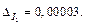 В окончательном результате оставим шесть значащих цифр:
В окончательном результате оставим шесть значащих цифр: 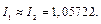 Тогда
Тогда
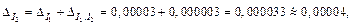
т. е. 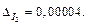 Следовательно,
Следовательно, 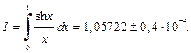
Пример 3. Вычислить с помощью формулы средних прямоугольников интеграл 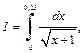 приняв
приняв 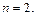 Определить абсолютную погрешность результата.
Определить абсолютную погрешность результата.
Решение. По заданным пределам интегрирования 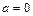 и
и 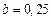 найдем шаг
найдем шаг  В данном случае точками разбиения отрезка
В данном случае точками разбиения отрезка 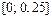 будут
будут 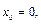
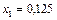 и
и 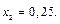 Тогда по формуле (33.21), где
Тогда по формуле (33.21), где 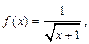 получим
получим

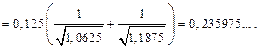
Находим абсолютную погрешность метода  Так как
Так как
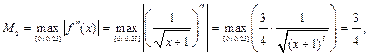
то, используя формулу (33.22), имеем

т. е. 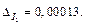 В окончательном результате оставим четыре значащие цифры:
В окончательном результате оставим четыре значащие цифры: 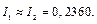 Тогда
Тогда
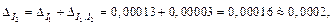
т. е. 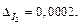 Следовательно,
Следовательно, 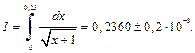
Для сравнения приведем точное значение интеграла: 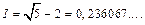
Пример 4. Вычислить с помощью формулы трапеций интеграл 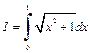 с точностью до
с точностью до 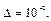
Решение. Для определения необходимого числа разбиений n оценим остаточный член  по формуле (33.24). Так как
по формуле (33.24). Так как
|
|
|
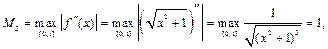
то 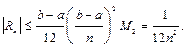
Решая неравенство

получим 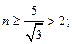 примем
примем 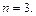
Зная пределы интегрирования, найдем шаг 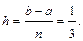 Точками разбиения служат
Точками разбиения служат 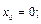
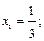
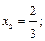
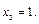 Найдем соответствующие значения подынтегральной функции
Найдем соответствующие значения подынтегральной функции 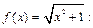
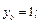
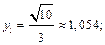
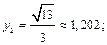
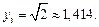 Тогда по формуле (33.23) получаем
Тогда по формуле (33.23) получаем
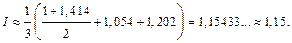
Следовательно, 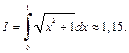
Для сравнения приведем точное значение интеграла: 
Пример 5. Вычислить с помощью формулы Симпсона интеграл 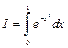 с точностью до
с точностью до 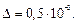
Решение. Для определения n оценим остаточный член  по формуле (33.26). Можно показать (проверить самостоятельно!), что
по формуле (33.26). Можно показать (проверить самостоятельно!), что
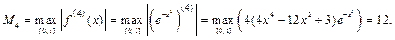
Поэтому
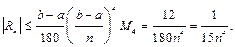
Решая неравенство
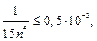
получим 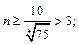 примем
примем 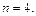
Нужно определить значения подынтегральной функции при 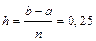 для следующих значений аргумента:
для следующих значений аргумента: 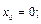

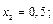
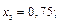
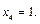 Найдем соответствующие значения
Найдем соответствующие значения 
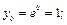
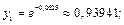
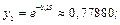
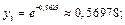
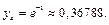 Тогда по формуле (33.25) получим
Тогда по формуле (33.25) получим
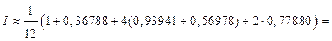
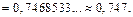
Следовательно, 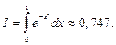
Задания
I уровень
1.1. С помощью степенных рядов вычислите интеграл с точностью до 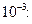
1)  2)
2) 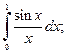
3) 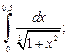 4)
4) 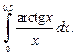
1.2. Пользуясь формулой левых прямоугольников при 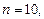 вычислите
вычислите 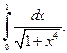
1.3. Пользуясь формулой правых прямоугольников при 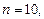 вычислите
вычислите 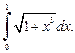
1.4. Используя формулу средних прямоугольников при 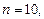 вычислите
вычислите 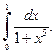
1.5. С помощью формулы трапеций при 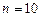 вычислите
вычислите 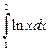 и определите абсолютную и относительную погрешности результата, зная точное значение интеграла.
и определите абсолютную и относительную погрешности результата, зная точное значение интеграла.
|
|
|
1.6. С помощью формулы Симпсона при 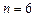 вычислите
вычислите 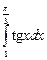 и определите абсолютную и относительную погрешности результата, зная точное значение интеграла.
и определите абсолютную и относительную погрешности результата, зная точное значение интеграла.
1.7. Определите, на сколько частей нужно разбить промежуток интегрирования, чтобы по формулам левых и правых прямоугольников с точностью до  вычислить
вычислить 
1.8. Определите, на сколько частей следует разбить промежуток интегрирования, чтобы по формуле средних прямоугольников с точностью до 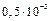 вычислить
вычислить 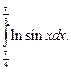
1.9. Определите, на сколько частей следует разбить промежуток интегрирования, чтобы по формуле трапеций с точностью до 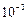 вычислить
вычислить 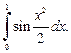
1.10. Ширина реки равна 20 м. Замеры глубины в поперечном сечении реки через каждые 2 м дали следующие результаты, указанные в следующей таблице:
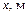
| |||||||||||
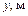
| 0,4 | 0,8 | 1,1 | 1,4 | 1,8 | 2,1 | 2,4 | 1,9 | 1,5 | 0,9 | 0,5 |
Здесь через x обозначено расстояние от одного из берегов, а через y – соответствующая глубина реки. Требуется найти площадь поперечного сечения реки.
II уровень
2.1. С помощью разложения подынтегральной функции в степенной ряд вычислите 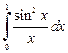 с точностью до
с точностью до 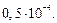
2.2. Вычислите 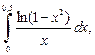 разлагая подынтегральную функцию в степенной ряд и используя три члена этого разложения. Определите абсолютную погрешность результата.
разлагая подынтегральную функцию в степенной ряд и используя три члена этого разложения. Определите абсолютную погрешность результата.
|
|
|
2.3. Вычислите с помощью формул левых и правых прямоугольников интеграл 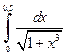 с точностью до
с точностью до 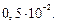
2.4. Вычислите 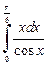 с точностью до
с точностью до 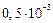 с помощью формулы средних прямоугольников.
с помощью формулы средних прямоугольников.
2.5. Вычислите 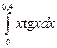 с точностью до
с точностью до 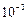 с помощью формулы трапеций.
с помощью формулы трапеций.
2.6. Вычислите 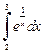 с точностью до
с точностью до 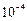 с помощью формулы Симпсона.
с помощью формулы Симпсона.
2.7. Найдите с точностью до 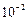 длину дуги косинусоиды
длину дуги косинусоиды 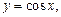
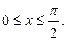
2.8. Найдите с точностью до 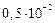 длину дуги лемнискаты Бернулли
длину дуги лемнискаты Бернулли 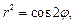
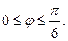
III уровень
3.1. Вычислите 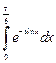 с точностью до
с точностью до 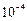 путем разложения подынтегральной функции в функциональный ряд.
путем разложения подынтегральной функции в функциональный ряд.
3.2. По формуле левых прямоугольников вычислите 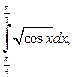 приняв
приняв  и определите абсолютную погрешность результата.
и определите абсолютную погрешность результата.
3.3. По формуле правых прямоугольников вычислите 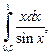 приняв
приняв  и определите абсолютную погрешность результата.
и определите абсолютную погрешность результата.
3.4. По формуле средних прямоугольников вычислите 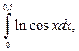 полагая
полагая 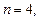 и определите абсолютную погрешность результата.
и определите абсолютную погрешность результата.
3.5. Пользуясь формулой трапеций при 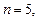 вычислите
вычислите 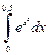 и определите абсолютную погрешность результата.
и определите абсолютную погрешность результата.
3.6. Пользуясь формулой Симпсона при  вычислите
вычислите 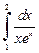 и определите абсолютную погрешность результата.
и определите абсолютную погрешность результата.
3.7. Найдите с точностью до 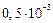 площадь фигуры, ограниченной кривой
площадь фигуры, ограниченной кривой  прямыми
прямыми 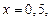
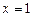 и осью Ox.
и осью Ox.
3.8. Составьте алгоритмическую схему приближенного вычисления определенного интеграла от функции, заданной таблично, по формулам левых и правых прямоугольников.
3.9. Составьте алгоритмическую схему приближенного вычисления определенного интеграла от функции, заданной таблично, по формуле средних прямоугольников.
3.10. Составьте алгоритмическую схему приближенного вычисления определенного интеграла от функции, заданной таблично, по формуле трапеций.
3.11. Составьте алгоритмическую схему приближенного вычисления определенного интеграла от функции, заданной таблично, по формуле Симпсона.
Дата добавления: 2015-12-17; просмотров: 23; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
