Метод наименьших квадратов
Пусть данные некоторого опыта представлены таблицей значений 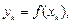
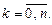 Требуется найти приближенную зависимость
Требуется найти приближенную зависимость
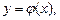 (33.13)
(33.13)
значения которой при 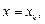
 мало отличаются от опытных данных
мало отличаются от опытных данных 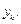 Приближенная функциональная зависимость (33.13), полученная на основании экспериментальных данных, называется эмпирической формулой.
Приближенная функциональная зависимость (33.13), полученная на основании экспериментальных данных, называется эмпирической формулой.
Мерой близости функций 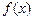 и
и 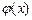 на множестве точек
на множестве точек 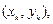
 при среднеквадратичном приближении является величина S, определяемая равенством
при среднеквадратичном приближении является величина S, определяемая равенством
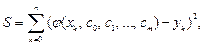
где 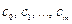 – постоянные параметры. При этом
– постоянные параметры. При этом 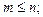 случай
случай 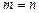 соответствует интерполяции.
соответствует интерполяции.
Метод наименьших квадратов состоит в том, что параметры 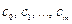 эмпирической формулы (33.13) находятся из условия минимума функции
эмпирической формулы (33.13) находятся из условия минимума функции 
Если функция 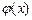 ищется в виде многочлена (33.7), то соответствующая система уравнений для отыскания коэффициентов многочлена
ищется в виде многочлена (33.7), то соответствующая система уравнений для отыскания коэффициентов многочлена 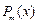 называется нормальной и имеет вид
называется нормальной и имеет вид
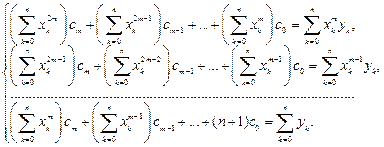
При 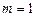 нормальная система уравнений запишется в виде
нормальная система уравнений запишется в виде
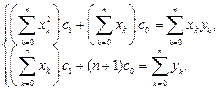 (33.14)
(33.14)
Возможность использования линейной зависимости можно проверить путем вычисления значений 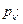
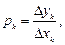
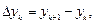
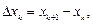

При 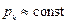 в качестве эмпирической формулы может быть выбрана у = ах + b.
в качестве эмпирической формулы может быть выбрана у = ах + b.
Пример 1. С помощью степенного ряда вычислить 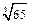 с точностью до ∆ = 10– 6.
с точностью до ∆ = 10– 6.
Решение. Очевидно, что
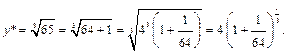
Воспользуемся биномиальным рядом
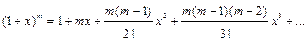
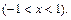
Полагая в нем 
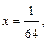 получаем
получаем
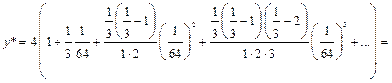
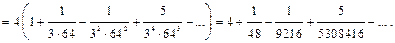
Полученный числовой ряд, начиная со второго члена, является знакочередующимся рядом, удовлетворяющим условиям признака Лейбница. Так как
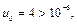
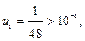
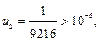
но 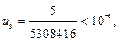 то отсюда имеем оценку остаточного члена:
то отсюда имеем оценку остаточного члена:
|
|
|
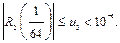
Поэтому для обеспечения заданной степени точности достаточно взять три члена ряда:
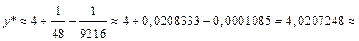
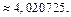
Следовательно, 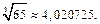
Пример 2. С помощью степенного ряда вычислить 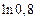 с точностью до ∆ = 10– 4.
с точностью до ∆ = 10– 4.
Решение. Воспользуемся разложением функции 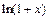 в ряд Маклорена
в ряд Маклорена
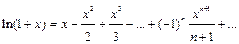
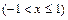
при х = – 0,2:
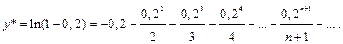
Определим n, используя остаточный член полученного числового ряда:
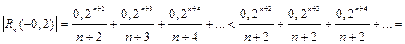
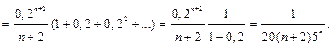
Путем подбора значений n находим, что для n = 3
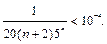
Поэтому здесь достаточно взять четыре члена ряда:
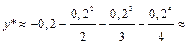
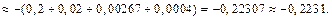
Следовательно, 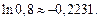
Пример 3. Найти интерполяционный многочлен Лагранжа для функции 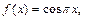 заданной в виде таблицы:
заданной в виде таблицы:
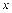
| 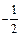
| 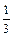
| 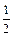
| |
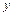
| 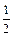
|
Определить абсолютную погрешность интерполяционного многочлена при 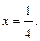
Решение. Применяя формулу (33.11) при 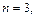 получим:
получим:

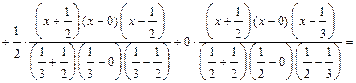
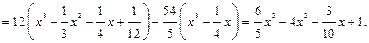
Итак, 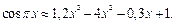
Оценим остаточный член многочлена Лагранжа по формуле (33.12) при 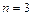 и
и 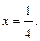 Так как
Так как
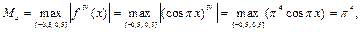
то 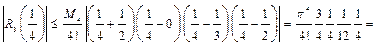
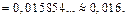
Следовательно, искомая абсолютная погрешность равна ∆ = 0,016.
Пример 4. Методом наименьших квадратов найти эмпирическую формулу, отвечающую таблице:
| x | |||||
| 8,5 | 11,5 |
Решение. Поскольку здесь 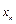 – равноотстоящие точки
– равноотстоящие точки  то достаточно вычислить разности
то достаточно вычислить разности 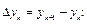
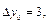
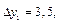
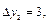
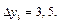 Так как эти разности мало отличаются друг от друга, то в качестве эмпирической формулы можно принять линейную зависимость
Так как эти разности мало отличаются друг от друга, то в качестве эмпирической формулы можно принять линейную зависимость 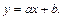
|
|
|
Результаты вычислений представлены в таблице:
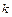
| 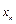
| 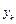
| 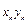
| 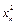
|
| 8,5 11,5 | 34,5 | |||
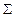
| 116,5 |
Нормальная система уравнений (33.14) в данном случае принимает вид:
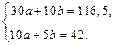
Решая эту систему, находим: 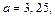
 Следовательно, искомая эмпирическая формула есть
Следовательно, искомая эмпирическая формула есть 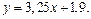
Задания
I уровень
1.1. Вычислите с помощью степенных рядов с точностью до 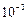 величину:
величину:
1)  2)
2)  3)
3) 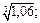
4) 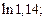 5)
5) 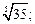 6)
6) 
1.2. Используя интерполяционный многочлен Лагранжа, найдите уравнение параболы, проходящей через точки 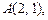
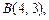
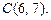
1.3. Составьте уравнение многочлена наименьшей степени, график которого проходит через точки 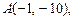
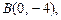
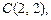
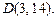
1.4. Найдите интерполяционный многочлен Лагранжа для функции 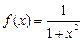 по ее значениям в точках
по ее значениям в точках 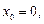
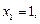
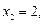
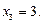
1.5. Функция 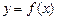 задана в виде таблицы:
задана в виде таблицы:
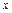
| ||||
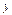
| –1 |
Пользуясь интерполяционным многочленом Лагранжа, вычислите 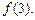
1.6. Функция 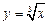 задана следующей таблицей:
задана следующей таблицей:
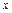
| 1,0 | 1,1 | 1,3 | 1,4 |
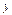
| 1,0000 | 1,0323 | 1,0914 | 1,1187 |
Используя интерполяционный многочлен Лагранжа, вычислите 
1.7. С помощью метода наименьших квадратов найдите эмпирические формулы, отвечающие приведенным таблицам:
| 1) | 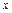
| ||||||
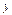
| 1,2 | 2,0 | 2,7 | 3,6 | 4,3 | 5,1 |
|
|
|
| 2) | 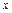
| –2 | –1 | ||||
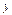
| 4,0 | 5,2 | 6,5 | 7,6 | 8,9 | 10,1 |
| 3) | 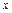
| |||||
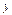
|
| 4) | 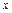
| 1,0 | 1,5 | 2,0 | 2,5 | 3,0 | 3,5 |
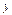
| 0,1 | 0,6 | 1,0 | 1,6 | 2,0 | 2,5 |
| 5) | 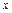
| –2 | ||||
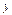
| –1,5 | 1,0 | 2,3 | 3,5 | 6,2 |
II уровень
2.1. Вычислите с помощью степенных рядов с точностью до 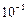 величину:
величину:
1) 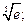 2)
2) 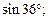 3)
3) 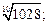 4)
4) 
2.2. Вычислите с помощью степенных рядов с точностью до 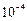 величину:
величину:
1) 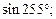 2)
2) 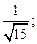 3)
3) 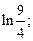 4)
4) 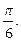
2.3. В прямоугольном треугольнике один из катетов равен 1 см, гипотенуза – 3 см. Найдите острый угол треугольника, лежащий против меньшего катета, с точностью до 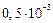 радиана.
радиана.
2.4. Определите, с какой точностью можно вычислить 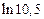 с помощью интерполяционного многочлена Лагранжа для функции
с помощью интерполяционного многочлена Лагранжа для функции  выбрав в качестве узлов интерполяции
выбрав в качестве узлов интерполяции 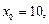
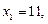
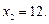
2.5. Зная значения функции 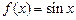 при
при 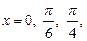
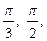 с помощью интерполяционного многочлена Лагранжа найдите
с помощью интерполяционного многочлена Лагранжа найдите 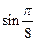 и оцените погрешность.
и оцените погрешность.
2.6. Постройте интерполяционный многочлен Лагранжа для функции 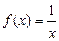 с узлами
с узлами 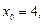
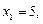
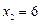 и покажите, что при
и покажите, что при 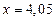 интерполяционный многочлен дает значение функции с тремя верными значащими цифрами.
интерполяционный многочлен дает значение функции с тремя верными значащими цифрами.
2.7. Дана таблица значений интеграла вероятности 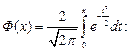
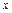
| 1,98 | 1,99 | 2,00 | 2,01 | 2,02 | 2,03 |
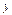
| 0,9523 | 0,9534 | 0,9545 | 0,9556 | 0,9566 | 0,9576 |
|
|
|
С помощью линейной интерполяции найдите Ф (2,004) и укажите оценку остаточного члена R 1(2,004).
2.8. Дана таблица значений функции 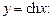
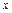
| 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 |
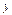
| 1,128 | 1,185 | 1,255 | 1,337 | 1,433 | 1,543 |
С помощью квадратичной интерполяции найдите 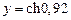 и укажите оценку остаточного члена
и укажите оценку остаточного члена 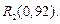
2.9. Найдите величину ускорения при равноускоренном движении тела, если известны значения пройденного им пути S в некоторые моменты времени t, которые указаны в таблице:
| ||||||

|
III уровень
3.1. Пользуясь формулой разложения в ряд Маклорена функции 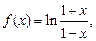 вычислите
вычислите 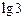 с точностью до
с точностью до 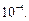
3.2. Монотонная функция 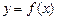 задана таблицей:
задана таблицей:
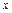
| 0,1 | 0,4 | 0,5 | 2,5 |
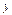
| 0,0 | 0,1 | 0,2 | 0,4 |
С помощью интерполирования найдите значение x, при котором 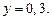
3.3. Дана таблица значений функции  при
при 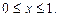 Определите, какова наибольшая погрешность линейной интерполяции
Определите, какова наибольшая погрешность линейной интерполяции 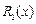 на отрезке
на отрезке 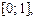 если шаг равен 0,01.
если шаг равен 0,01.
3.4. Пусть требуется составить таблицу значений функции 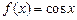 на отрезке
на отрезке  Выясните, какой величины должен быть шаг h таблицы, чтобы при линейной интерполяции погрешность интерполяции была меньше, чем
Выясните, какой величины должен быть шаг h таблицы, чтобы при линейной интерполяции погрешность интерполяции была меньше, чем 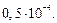
3.5. Дана таблица значений функции 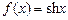 при
при 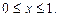 Выясните, какова наибольшая погрешность квадратичной интерполяции
Выясните, какова наибольшая погрешность квадратичной интерполяции 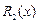 на отрезке
на отрезке 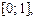 если шаг равен 0,1.
если шаг равен 0,1.
3.6. Составьте алгоритмическую схему вычисления в точке x приближенного значения функции, заданной таблично, с помощью интерполяционного многочлена Лагранжа.
3.7. Составьте алгоритмическую схему вычисления в точке x приближенного значения функции, заданной таблично, с помощью эмпирической формулы в случае линейной зависимости.
Дата добавления: 2015-12-17; просмотров: 21; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
