Интегрирование с помощью рядов
Предположим, что подынтегральная функция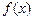 
разлагается в степенной ряд
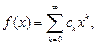(33.19)
сходящийся в интервале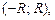 
который содержит отрезок интегрирования 
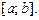Тогда искомый интеграл I можно представить в виде числового ряда
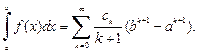(33.20)
Используем непрерывную аппроксимацию для функции 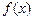и в качестве аппроксимирующей функции 
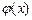возьмем n -ю частичную сумму ряда (33.19):
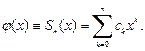
Если ряд (33.20) знакочередующийся, то для оценки его остаточного члена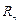 
можно воспользоваться известным следствием признака Лейбница. В случае знакопостоянного ряда (33.20) обычно применяется мажорирование 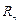бесконечно убывающей геометрической прогрессией.
Дата добавления: 2015-12-17; просмотров: 23; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!