Показатели колеблемости (вариации) значений признаков.
Для характеристики рядов распределения оказывается недостаточным указание только средней величины данного признака, поскольку два ряда могут иметь, к примеру, одинаковые средние арифметические, но степень концентрации (или, наоборот, разброса) значений признаков вокруг средней будет совершенно различной. Характеристикой такого разброса служат показатели колеблемости — разность между максимальным и минимальным значениями признака в некоторой совокупности (вариационный размах), а также другие показатели: среднее абсолютное (линейное) отклонение, среднее квадратическое отклонение и т. п.
Дисперсия. Дисперсией называется величина, равная среднему значению квадрата отклонений отдельных значений признаков от средней арифметической. Обозначается дисперсия s2 и вычисляется но формуле,

Корень квадратный из дисперсии называется средним квадратическим отклонением и обозначается s.
Геометрически среднее квадратическое отклонение является показателем того, насколько в среднем кривая распределения размыта относительно ее среднего арифметического. Измеряется в тех же единицах, что и изучаемый признак.
При ручном счете для упрощения вычислений дисперсию Ы рассчитывают по формуле методом отсчета от условного нуля. Для интервального ряда с равными интервалами процедура следующая. Сначала вычисляются центры интервалов. Относительно какого-либо отобранного серединного интервала ряда, например А, вверх и вниз выписывается натуральный ряд чисел (аi) соответственно со знаком «плюс» и «минус»: 0, +1, +2 и т. д.; —1, —2 и т, д. (табл. 4).
|
|
|
В качестве промежуточного результата по формуле (7) получаем среднее арифметическое. Величина дисперсии получается подстановкой промежуточных величин из табл. 4 в формулу (8).
Среднее арифметическое находится по формуле19

Приведенные вычисления показывают, что при среднем возрасте» 40 лет все остальные члены совокупности имеют возраст, который в среднем отклоняется от 40 лет на 7,8 лет, т. е. примерно на 20%.

Среднее абсолютное отклонение. Эта мера вариации представляет собой среднее арифметическое из абсолютных величин отклонений отдельных значений признака от их среднего арифметического, нения часто выражаются через соотнесение в процентах к среднему арифметическому, т. е. в виде относительных величин.
Отношение среднего линейного или среднего квадратического отклонения к среднему арифметическому называется коэффициентом, вариации (V):

Очевидно, что тот из рядов имеет большее рассеяние, у которого коэффициент вариации больше.
Рассмотренные выше показатели вариации применимы лишь к количественным признакам, а точнее к признакам, измеренным не ниже чем по интервальной шкале. Применение этих мер для низших уровней, строго говоря, некорректно и требует тщательной интерпретации полученных результатов.
|
|
|
Вариации качественных признаков. Если признак имеет k взаимоисключающих градаций, то для вычисления индекса качественной вариации применяется процедура, поясняемая следующим примером.
Пусть получено следующее распределение ответов (взаимоисключающих) па вопросы А, В и С(колонка 1):
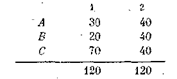
Во вторую колонку запишем такие частоты, которые получились бы при равномерном заполнении всех трех вопросов, т. е. 120/3 = 40. Теперь вычислим величину
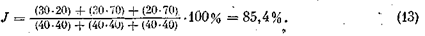
Этот показатель называется индексом качественной вариации и указывает на степень неоднородности полученных ответов. Если бы все ответы попали лишь в одну градацию, то j = 0, что означало бы полное единство в ответах, хотя, конечно, индекс совершенно не учитывает того, в какую именно градацию попали все эти ответы.
Совершенно аналогично индекс вычисляется при любом числе градаций. Но для альтернативных признаков вариация обычно подсчитывается по формуле (14). Она отличается от J на константу, называется дисперсией, выражается в абсолютных числах и обозначается s2:
|
|
|
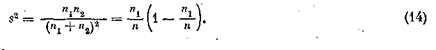
Другой мерой вариации признака (независимо от уровня измерения) может служить так называемая энтропия — мера неопределенности, вычисляемая по формуле
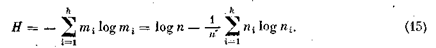
Логарифм в этой формуле может быть взят по любому основанию. Энтропия обладает следующими свойствами:
а) энтропия равна нулю лишь в том случае, если вероятность получения одного из значения x i признака х равна единице (вероятность остальных значений при этом равна нулю). Такой признак не обладает неопределенностью, так как достоверно известно одно единственно возможное его значение. Во всех остальных случаях, когда имеется та или иная неопределенность в значениях x i, энтропия является положительной величиной;
б) наибольшей энтропией обладает признак, когда все значения x i равновероятны. Для признака с k градациями

Отсюда видно, что максимальная энтропия увеличивается с ростом числа градаций в признаке.
Дата добавления: 2018-10-26; просмотров: 236; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
