Коэффициенты взаимозависимости для номинального

 уровня из­мерения.

Связь в табл. 2 X 2. Простейшая задача о взаимозависимости возникает тогда, когда имеются два признака, каждый из которых принимает два значения (табл. 13).

Представим данные о группировке по этим двум признакам так;

Для характеристики степени связи двух признаков применяется коэффициент Ф, определяемый формулой

Коэффициент Ф равен 0, если нет соответствия между двумя дихотомическими переменными, и равен 1 или —1, когда имеется полное соответствие между ними. В силу трудностей. с интерпрета­цией знака коэффициента для катетеризованных (поминальных) переменных часто используют в анализе лишь абсолютную величи­ну—|Ф|. Ф легко интерпретируется, поскольку показано, что он представляет собой просто коэффициент корреляции r, если значе­ния каждой дихотомической переменной обозначить 0 и 1.

Как уже отмечалось, Ф вычисляется для катетеризованных дан­ных, представляющих естественные дихотомии: пол, раса, и т. п. Приведение количественных переменных к дихотомическому виду связано .с выбором граничной точки разделения (например, мужчи­ны до 30 лет и мужчины старше 30 лет). Искусственная дихотомизация, столь часто необходимая в конкретном исследовании при изучении взаимосвязи признаков, может привести к тому, что одна часть дихотомической переменной по своему воздействию будет бо­лее значима для одной связи, другая —для другой, а это даст оши­бочный результат.

Измерение связи в табл. с X k. Рассмотрим теперь более общую ситуацию, когда две переменные классифицированы па две или более категории. Запишем это таким образом:

где n_ij частоты; n_i— маргинальные суммы частот по строкам; n_j— маргинальные суммы частот по столбцам. На с. 169—172 для выяс­нения отклонения от независимости распределения значений в по­добном случае использовался критерий c². Однако сама величина c²не очень подходит в качестве меры связи, поскольку сильно зависит от числа категорий.

Нормированным коэффициентом корреляции для таблицы c X k является коэффициент сопряженности Пирсона (P)

Коэффициент Р = 0 при полной независимости признаков. Недо­статком, его является зависимость максимальной величины Р от размера таблицы (максимум Р достигается при c = k, но сама гра­ница изменяется с изменением числа категорий). В связи с этим возникают трудности сравнения таблиц разного размера.

Чтобы исправить указанный недостаток, Чупров ввел другую величину:

При с = kТ достигает +1 в случае полной связи, однако не обла­дает этим свойством при k не равно с.

Коэффициент Крамера (К) может всегда достигать +1 незави­симо от вида таблицы:

Для квадратной таблицы коэффициенты Крамера и Чупрова совпа­дают, а в остальных случаях К > Т.

Величина c² быстро вычисляется с помощью формулы

Вычисление коэффициентов Р, Т и К связано с теми же ограни­чениями на х², которые сформулированы на с. 172.

Следующая группа коэффициентов связи для категоризованных данных основана на предположении, что если две переменные свя­заны, то информация об одной переменной может быть использо­вана для предсказания другой. Так, если предположить, что связь между полом индивида и его отношением к правилам уличного движения абсолютно детерминирована, то согласно табл. 13 либо все мужчины были бы нарушителями, а женщины нет, либо наоборот. Поскольку это не так, то возникает несоответствие, или, как говорят, ошибка предположения абсолютной связи (обозначим величину этой ошибки 0 _А).

С другой стороны, можно предположить, что два признака абсо­лютно не связаны, и нельзя на основе одной переменной предска­зать другую. Поскольку это тоже не так, то возникает ошибка предположения об отсутствии связи (0₀).

может служить мерой относительного уменьшения ошибки при- использовании информации об одной пе­ременной для предсказания другой.

Признак, на основе которого предсказывается другой признак, будем называть независимой переменной, а предсказываемый — за­висимой.

Тогда для случая, когда зависимая переменная расположена по строкам таблицы (т. е. Категории расположены по строкам), вычис­ляется коэффициент связи l _г:

где max n — наибольшая частота в столбце r; max n j — наибольшая маргинальная частота для строк j.

Пример. Вычислим К₂для данных табл. 13 в предположении, что K₁ независимая переменная, а отношение к правилам уличного движения — зависимая

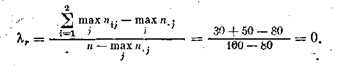
Таким образом, использование информации о поле обследованных для предсказания отношения к правилам движения не умень­шает относительной ошибки.

Если зависимая переменная — это категории столбцов таблицы, то совершенно аналогично предыдущему вычисляется

где mах n_ij — наибольшая частота в строке; max n_i— наибольшая

маргинальная частота для столбцов i.

Для нашего примера, когда пол зависимая переменная, l = 0,4, т. е. получаем 40%-пое уменьшение в ошибке, если используем от­ношение к правилам в качестве предсказывающей пол нарушителя.

Коэффициенты А и К имеют пределы изменения от 0 до 1. Чем ближе К _г или К _с к 1, тем больше относительное уменьшение в ошиб­ке и большее соответствие (связь) между переменными. Эти коэф­фициенты могут быть использованы для таблиц любого размера.

В ряде случаев удобно использовать симметричную l:  

Разнообразие корреляционных коэффициентов продиктовано стремлением отразить реально существующее разнообразие типов связей в природе и обществе. Поэтому данное обстоятельство сле­дует рассматривать скорее как свидетельство достоинств статисти­ческого аппарата, заключающихся в гибкости и большой приспособ­ленности его к анализу сложнейших взаимосвязей в социальной области. Каждый корреляционный коэффициент приспособлен дли измерения вполне определенного вида связи. Техника расчета и конструкция формулы одного и того же коэффициента могут изме­ниться в зависимости от того, какие (например, сгруппированные или не сгруппированные) данные приходится анализировать. Срав­ните, например, различные варианты формул для парного коэффи­циента корреляции r. Таким образом, применение того или иного показателя определяется природой данных и формой их представ­ления. Требуемая степень точности также может существенно по­влиять на выбор способа расчета связи в каждом конкретном слу­чае. Обычно оценка пригодности той или иной формулы произво­дится с учетом следующих факторов:

1) природы данных (качественные или количественные при­знаки);

2) формы и типа зависимости (линейная или нелинейная, поло­жительная или отрицательная связь);

3) требуемой точности расчетов (например, коэффициенты кор­реляции рангов rи t иногда могут использоваться вместо более точных мер rи t²);

4) удобства при вычислении и сравнительной простоты интер­претации;

5) трудностей технического порядка (имеется ли счетная техни­ка или нужно вести расчеты вручную);

6) распространенности использования того или иного коэффици­ента корреляции;

7) возможности сравнения различных коэффициентов.

Обычно предпочитают использовать наиболее распространенные в практике социологических исследований коэффициенты, так как тем самым достигается возможность сравнения полученных резуль­татов с материалами других исследований.

 

---

Дата добавления: 2018-10-26; просмотров: 230; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!