Глава 3. ОЦЕНКА КАЧЕСТВА СПЕЦИФИКАЦИИ МОДЕЛИ

 

Анализ погрешностей исходной информации

 

Значения экономических показателей обычно известны неточно, с некоторой погрешностью. Рассмотрим основные правила обработки данных, содержащих погрешности, или ошибки измерений. Пусть число a представляет точное (неизвестное нам) значение некоторой величины, а x_i ( i=1,2,…, n) – известные приближенные значения той же величины, при этом   

  x_i= a+e _i ,                                                                       (12.1)

 где e _i – погрешность i-го измерения. Значения погрешностей e _i нам неизвестны, т.к. неизвестно точное значение a, но, как правило, удается оценить модуль разности

                  | x_i – a|<e .                                                                     (12.2)

Величину e > 0 называют предельной абсолютной погрешностью, или короче, абсолютной погрешностью. Если a≠0 , то можно ввести относительную погрешность
 δ=e /| a|. На практике величину относительной погрешности вычисляют по формуле
δ =e /| 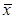|, полагая 

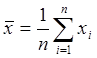.                                                                 (12.3)

Принято использовать запись a= x ±e как условную запись неравенства      

           x-e< a< x+e                                                                       (12.4)

и запись a= x(1 ±δ) как сокращенную запись неравенств

                      x(1-δ)< a< x(1+δ) .                                                             (12.5)

Величина относительной погрешности δ связана с числом верных десятичных знаков числа x. Рассмотрим этот вопрос на простых примерах. Число a=51.0±0.5 имеет два верных десятичных знака. Поэтому относительная погрешность δ=0.5/51≈0.01 или 1%. Число b=0.51±0.005 также имеет два верных знака и ту же относительную погрешность δ=1%. Если число задается с тремя верными знаками, то относительная погрешность будет иметь порядок 0.1%. Например, если a=510±0.5, то δ=0.001 или 0.1%. Рассматривая в качестве примеров числа 110 и 910 (с тремя верными знаками), нетрудно проверить, что относительная погрешность δ этих величин будет меняться в пределе от 0.05% до 0.5%. При двух верных десятичных знаках относительная погрешность изменяется в диапазоне 0.5% ¸5%.

Различают погрешности (ошибки) систематические и случайные. Если часы спешат или отстают, то они показывают время с некоторой систематической ошибкой. Для ее устранения нужно узнать точное время и выставить часы правильно. В общем случае для устранения систематической ошибки либо заменяют измерительный прибор на более точный, либо вводят поправку на систематическую ошибку (в астрономии, навигации и т.п.).

Анализ случайных ошибок проводится с применением методов теории вероятности и математической статистики. Пусть величина e _i в равенстве (12.1) является случайной величиной, распределенной по нормальному закону с математическим ожиданием Ee _i=0 и дисперсией De _i =s ², что принято записывать как e _i Î N(0, s ²).

Измеренные значения x_i также являются случайными величинами, при этом Ex_i= a, Dx_i=s ². Интуиция подсказывает нам, что среднее арифметическое (12.3) является лучшей оценкой для величины a, чемотдельные наблюдения x_i .   Действительно, 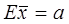 - оценка является несмещенной, а дисперсия среднего  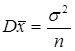   при n®∞ стремится к нулю. Величину дисперсии измерений s ² можно оценить по данным x_i известными формулами

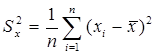                                                                       (12.5)

или

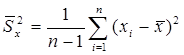                                                                         (12.6)

При этом оценка (12.5) является смещенной оценкой дисперсии s ², так как известно [3], что 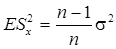. Оценка (12.6) несмещенная: 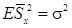. В теории ошибок величина  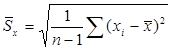 называют средней квадратичной ошибкой серии наблюдений {x_i}, а величина 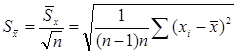- средней квадратичной ошибкой среднего арифметического.

 

Доверительные интервалы

 

Введем случайную величину      

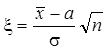.                                                        (13.1)

Нетрудно проверить, что x ÎN(0,1), вследствие чего

.

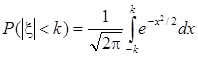Полагая 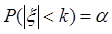, получим после элементарных преобразований, что с

вероятностью a выполняется неравенство

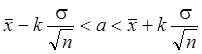                 .                                    (13.2)

 Интервал 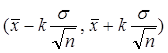 называется доверительным интервалом, отвечающим доверительной вероятности a . Если, к примеру, k=2, доверительная вероятность a=0.955. Значению k=3 отвечает вероятность a = 0.997 (правило «трех сигм»). Но для использования указанных доверительных интервалов на практике нужно знать стандартное отклонение s. Если значение s неизвестно, для его оценки используется величина 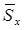. В этом случае можно ввести случайную величину

,

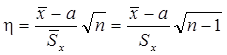которая имеет распределение Стьюдента с n-1 степенью свободы [3]. Не выписывая здесь соответствующей функции распределения, приведем несколько значений доверительной вероятности a( k, n), отвечающих доверительному интервалу 

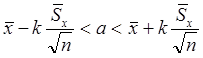                               .                                     (13.3)

При k=2 и n=3 имеем a=0.817; при k=2 и n=7 вероятность a=0.908  ;

a(3,3)=0.905; a(3,5)=0.96. С ростом n различие между распределением Стьюдента и Гауссовым распределением становится меньше, при n=20 этим различием в большинстве случаев можно пренебречь.

  Регрессионные модели мы строим по данным наблюдениям (x _i, y_i), i = 1,2,....n. Пусть значения x = x^* не совпадают с x _i. Чему будет равна величина y = y^* и с какой погрешностью ее можно найти?

  Попытаемся ответить на этот вопрос для случая парной линейной регрессии с нулевым свободным членом

                                      y_i = bx_i + e_i ,

где e_i Î N(0,s), i = 1,2...n.

Параметр b оцениваем методом наименьших квадратов:

                                     Se_i² = S(bx_i – y_i)² ® min,

                                       S(bx_i – y_i)x_i = 0,

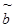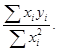            =                                                                  (13.4)

Из формулы (13.4) следует, что оценка 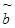 является гауссовой случайной величиной с математическим ожиданием 

E 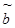=  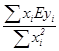=  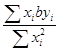= b

(оценка несмещенная) и дисперсией

                             D 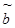 =  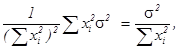                                      (13.5)

Величина σ² , как правило, неизвестна и ее следует оценить. Для этого составим сумму квадратов ошибок 

            Se_i² = S(bx_i – y_i)² = S(b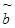x_i – x_i + 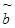x_i - y_i)²  =

        = Sx_i²(b- 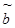)² + Σ( 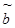x_i –y_i)²+ 2Sx_i(b- 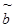)( 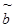x_i- y_i).                                       (13.6)

Математическое ожидание ESe_i² = SЕe_i² = nσ².

Вычисление математического ожидания в правой части равенства (13.6) дает

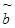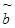                             Sx_i² D  + EΣ( x_i –y_i)²,

так как математическое ожидание последнего слагаемого равно нулю. Поэтому

nσ² = Sx_i² D 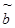 + EΣ( 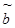x_i –y_i)².

С учетом формулы (13.5) получим 

(n-1)σ² = EΣ( 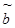x_i –y_i)² .

Теперь ясно, что величина 

                                   S ² = 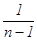 Σ( 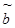x_i –y_i)²                                            (13.7)

будет несмещенной оценкой для σ². Множитель (n-1) указывает на то, что, располагая только одним наблюдением (x_1, y₁), нельзя получить оценку S ², так как возникает неопределенность вида 0/0.

Для определения доверительного интервала оценки 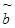, отвечающего доверительной вероятности α, рассмотрим случайную величину

ξ = ( b- ) ,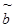

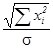имеющую нормальное распределение N(0,1). Заменив σ оценкой S , придем к случайной величине

η = ( b- ) ,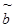

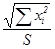имеющей распределение Стьюдента с (n-1) степенями свободы. Для прогнозируемого значения y*  регрессионная модель дает значение           

y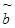^* = x^* + e,

 

при этом    Ey^* = bx^*,     Dy^*=( x^*)²D 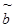 + De = σ² .

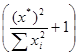Заменим дисперсию σ² оценкой S²  из (13.7):

( S_y^*)² = S ² .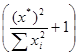

Доверительный интервал для прогнозируемых величин y^*   будет определяться распределением Стьюдента. Его границы вычисляются по формуле                   

                                                  y = y^* ± S_y^* t( n-1, 1-a/2),

где a - доверительная вероятность (например, a = 0,95), (n-1) – число степеней свободы. Статистические пакеты вычисляют эти границы и дают их графическое представление.

Совершенно аналогично рассматривается общий случай множественной линейной регрессии

y = Fq + e.

Можно показать, что

Dy^* = ( x^*) ^T Q x^* + s²,

где x_i = (x₁,x₂,...x_n)^*; Q = cov q =  s²(F^TF)^-1. Поэтому

Dy^* = s²[( x^*) ^T (F^TF)^-1x^* +1].

Несмещенной оценкой для s ² является число

S ² = 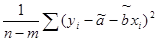.                                         (13.8)

Поэтому оценка среднеквадратичного отклонения y^*  будет

S_y^* = S[( x^*) ^T (F^TF)^-1x^* +1]^1/2,

 а граница доверительного интервала 

y = y^* ± S_y^* t( n- m, 1-a/2).

 

Расчет погрешностей

 

Эмпирические данные часто подвергаются математической обработке – над ними

выполняются арифметические операции сложения, вычитания, умножения и деления, в некоторых случаях производится логарифмирование, возведение в степень и др. Как это может сказаться на погрешности результата?

Покажем, что абсолютная погрешность суммы не превосходит суммы абсолютных погрешностей слагаемых. Пусть S= x+ y, причем слагаемые x, y известны с абсолютной погрешностью e_x,e_y, так что

,

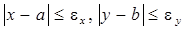где a и b – точные значения слагаемых. Для вычисления абсолютной погрешности суммы S оценим разность:

.

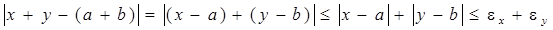Ясно, что в качестве предельной абсолютной погрешности суммы можно принять величину

                                                     e_S = e_x+e_y .                                               (14.1)

 

Аналогично проверяется, что абсолютная погрешность разности двух чисел d= x- y равна сумме абсолютных погрешностей уменьшаемого и вычитаемого: e_d = e_x+e_y. Заметим, что если числа x  и y мало отличаются между собой, относительная погрешность их разности d_d=e_d / | x- y|  может оказаться весьма большой.

При вычислении суммы S= x₁+ x₂+…+ x_n большого числа слагаемых, имеющих одинаковую абсолютную погрешность e, в соответствии с формулой (14.1) имеем

 

                                                       e_S = ne .                                                    (14.2)  

 

При n>>1 величина e_S может оказаться довольно большой. Но эта оценка получается в

предположении, что ошибки всех слагаемых максимальны и имеют одинаковый знак, что представляется мало вероятным. Более естественным выглядит предположение, что ошибка e является случайной и распределена по нормальному закону 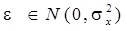, причем ошибки отдельных слагаемых являются независимыми случайными величинами. По правилу вычисления дисперсии сумма независимых случайных величин находим, что:  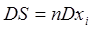    или 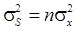  , так что .                                        

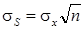При больших n (например, n=100) статистическая оценка дает значительно меньшее значение, чем предельная (14.2). Напомним, что отклонение случайной величины S от истинного значения более чем на 2 s _S возможно с вероятностью 0,045 (4,5%), а на 3s_S – с вероятностью 0,003 или 0,3%.

Для вычисления погрешности произведения и частного двух положительных чисел x, y рассмотрим сначала общий случай функции двух переменных u= f( x, y) (аналогично рассматривается случай функций многих переменных). Пусть переменная x известна с погрешностью e_x, переменная y – с погрешностью e_y. Приращение функции Du заменим дифференциалом

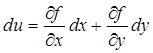                     ,                                                   (14.3)

полагая величины e _x и e _y достаточно малыми. Отсюда следует, что абсолютная погрешность e _u  функции u оценивается по формуле:

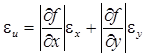               .                                                       (14.4)

В статистической теории предполагают ошибки e_x и e_y независимыми случайными величинами. Для дисперсии величины du имеем формулу

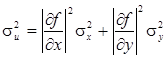                              .                                                  (14.5)

В случае произведения двух положительных чисел u= xy формула (14.4) дает оценку

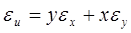                               ,                                              (14.6)

 а по формуле (14.5) получим

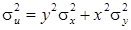             .                                             (14.7)

Для относительной погрешности произведения d _u= e _u / xy из формулы (14.6) следует, что

                             d_u=d_x+d_y ,                                                    (14.8)

 а из формулы (14.7) : 

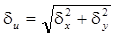              .                                            (14.9)

Пусть надо перемножить n положительных чисел x₁, x₂, …, x_n, заданных с одинаковой относительной погрешностью d. Формула (14.8) дает оценку d_u= nd , а по формуле (14.9) получаем .

Нетрудно убедиться в том, что для относительной погрешности частного U= x/ y двух положительных чисел x, y также справедливы формулы (14.8) и (14.9).

Если требуется найти значение функции U= f( x) одной переменной x, то вместо формулы (14.3) имеем (в первом приближении) 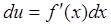 так что . Такой же результат следует из статистического анализа:

.

 

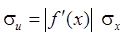Коэффициент детерминации

 

Коэффициент детерминации 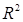 характеризует качество регрессионной модели. 

Значения различных величин, полученных расчетами, будем в дальнейшем обозначать «~».

Рассмотрим случай парной регрессии 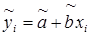. Имеет место равенство 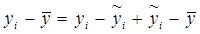. Для суммы квадратов отклонений y_i от среднего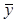

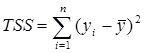 (TSS – total sum of squares)

имеем TSS = RSS+ESS, где 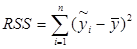 - сумма квадратов отклонений, объясненная регрессией (RSS — regression sum of squares),  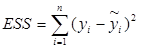- остаточная сумма квадратов отклонений (ESS – error sum of squares).

Коэффициент детерминации определяется по формуле:     

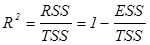.                                     .                                                       (15.1) 

 

Из (15.1) видно, что R²Î[0,1] и чем меньше R² отличается от 1, тем лучше регрессионная модель. 

В математической статистике вводится выборочный коэффициент корреляции 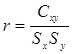 между данными наблюдений ( x_i, y_i), i=1, 2, …, n. Напомним, что     , ,

                        .

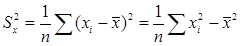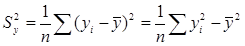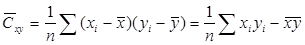Поскольку 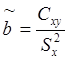, величину r можно представить в виде 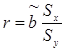. С другой стороны 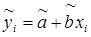, , 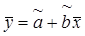откуда следует, что 

.

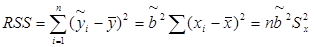Поэтому 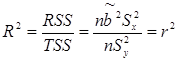, т.е. коэффициент детерминации равен квадрату выборочного коэффициента корреляции .

 

 

Средняя ошибка аппроксимации

 

Фактические значения интересующей нас величины отличаются от рассчитанных по уравнению регрессии. Чем меньше это отличие, чем ближе рассчитанные значения подходят к эмпирическим данным, тем лучше качество модели. Величина отклонений фактических и расчетных значений переменной величины по каждому наблюдению представляет собой ошибку аппроксимации. Так как отклонение может быть величиной как положительной, так и отрицательной, то ошибки аппроксимации для каждого наблюдения принято определять в процентах по модулю.

Отклонения ( 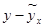) рассматриваются как абсолютная ошибка аппроксимации, тогда  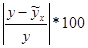– относительная ошибка аппроксимации.

Средняя ошибка аппроксимации определяется как среднее арифметическое: 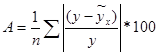. Иногда пользуются определением средней ошибки аппроксимации, имеющим вид .

 

---

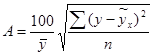Дата добавления: 2018-10-26; просмотров: 410; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!