Определение составляющих временного ряда

 

Одним из наиболее распространенных способов моделирования тенденции временного ряда является построение аналитической функции, характеризующей зависимость последовательных значений ряда от времени, или тренда. Этот способ называется аналитическим выравниванием временного ряда.

Для построения трендов чаще всего применяются следующие функции:

ü линейная y = a+ bt;

ü гиперболическая  ;     

ü экспоненциальная ;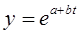

ü степенная: y = a t^b ;

ü многочлен n-ого порядка: y = a+ b₁ t+ b₂ t²+…+ b_n tⁿ.

Параметры каждого из перечисленных выше трендов можно определить методом наименьших квадратов, используя в качестве независимой переменной время t, а в качестве зависимой переменной – фактические значения временного ряда y_t. Для нелинейных трендов предварительно проводят стандартную процедуру их линеаризации.

Существует несколько способов определения типа тенденции. К числу наиболее распространенных относятся качественный анализ изучаемого процесса, построение и визуальный анализ графика зависимости значений ряда от времени.

Для анализа периодической составляющей временного ряда можно использовать аппарат тригонометрических рядов Фурье

                     ,                                 (8.1)

где T – полупериод, т.е. x( t+2T) = x( t), а коэффициенты ряда a_k, b_k вычисляются по

формулам:  

 

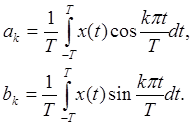         .                                                 (8.2)

В частности, при Т = p получаем тригонометрический ряд 

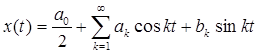                          .                            (8.3)

при этом коэффициенты a_k , b_k  будут равны

                                      

Если функция x (t) четная, т.е. выполняется равенство x (- t) = x (t), то в (8.1), (8.3)

 b_k = 0, а для коэффициента a_k получим формулу: . Если же функция x (t) нечетная, так что x (- t) = - x (t ), то a_k = 0, а для коэффициента b_k получим          .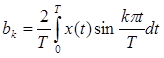

Если функция x(t) задана только в промежутке (0,T ), то ее можно продолжить в промежуток (- T, T ) четным или нечетным образом и следовательно, представить в виде ряда Фурье только по косинусам     

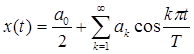
или только по синусам:

 

.

 

 

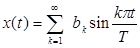Временной ряд как случайный процесс

 

Пусть значение экономического показателя x( t)в любой момент времени t представляет собой случайную величину X (t ).  Предположим, что случайная величина
 X (t)  является непрерывной. Тогда существует плотность вероятности f (x, t), по которой определяется вероятность случайного события  

.

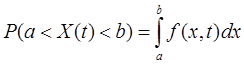Рассмотрим также математическое ожидание

       

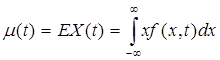                                                                              (9.1)

 и дисперсию

                .                         (9.2)

  Если плотность вероятности f ( x, t )= f (x) не зависит от времени, то математическое ожидание и дисперсия будут постоянными величинами.

  Рассмотрим два произвольных момента времени t₁ и t₂. Случайные величины X (t₁) и
 X (t₂) харатеризуются плотностью совместного распределения вероятностей
 f (x₁,t₁; x₂,t₂). При этом ковариация cov (X(t₁),X(t₂))  вычисляется по формуле

                             

 .

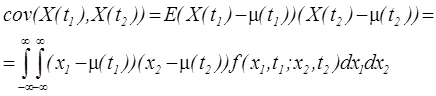   Аналогично рассматривается значение случайного процесса X (t) в трех, четырех и более точках t_k, при этом вводится многомерная плотность распределения f (x₁, t₁; x₂, t₂; …, x _m,t _m,).

   Случайный процесс называется стационарным, если при сдвиге по времени на произвольную величину T  функция распределения (а значит и плотность) не изменится . В этом случае плотность f (x, t) не зависит от времени: f (x, t) = f (x, t+ T) = f (x,0), а двумерная плотность f (x₁, t₁; x₂, t₂) зависит от разности t = t₁-t₂. Введя автокорреляционную функцию случайного процесса  K(t )= cov( X( t), X( t+ t)) , можно доказать, что для нее выполняются следующие свойства:

         1) K(- t ) = K(t );

        2) | K(t )| £ K(0);

        3) K (0 ) = DX.
Иногда функцию K(t )называют автоковариационной, а термин «автокорреляция» связывают с нормированной величиной r(t )= K(t )/ K(0).

Напомним, что для стационарного случайного процесса математическое ожидание
m = EX( t) и дисперсия DX = E( X( t)- m)² являются постоянными величинами. Если о случайном процессе известно, что EX  и DX постоянны, а корреляционная функция зависит только от t ( и не зависит от t), то случайный процесс называется стационарным в широком смысле.

  Пусть значения временного ряда x_t  ( t = 1,2,...n) являются равноотстоящими по времени значениями стационарного случайного процесса X( t) с математическим ожиданием μ = EX( t) и корреляционной функцией K(τ) = E( X( t), X( t+τ)), при этом дисперсия DX = K(0) º σ². Несмещенной оценкой величины m является среднее по времени

                 

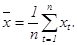
В качестве оценки корреляционной функции K(τ)при t = 0,1,2,...n-1 принимается величина

      

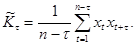
     Важной характеристикой стационарного случайного процесса является спектральная плотность  

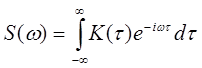 .                                 (9.3)

 

Из (9.3) следует, что

.

 

Вследствие четности функции K( t) справедлива формула:  

                                            .

 Для S(ω) принимается оценка

,

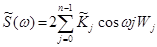где весовые коэффициенты W_j вводятся для сглаживания случайных осцилляций вычисляемых значений S(ω). На практике вычисление корреляционных функций и спектральной плотности выполняется с использованием статистических компьютерных пакетов, например, системы STATISTICA.

Модели ARIMA

 

В эконометрике анализ временных рядов с использованием оценки спектральной плотности (спектральный анализ) играет, как правило, вспомогательную роль, помогая установить периоды характерных циклов. Наибольшее распространение получили параметрические модели стационарных случайных процессов – модели авторегрессии и скользящего среднего.

Пусть X_t – значения стационарного случайного процесса, m = EX_t, x_t = X_t - m.. Введем случайный процесс x(t) ÎN(0,s²), для которого Ex_t = 0, Dx_t= s², Ex_tx_t-t= 0  (t¹0). Случайный процесс x_t будем называть белым шумом. В шкале непрерывного времени ему отвечает обобщенный случайный процесс x(t), спектр плотности которого S(τ) = const, при этом корреляционная функция K(τ) = 0 при τ ≠ 0. При τ = 0 корреляционная функция принимает бесконечно большое значение, точнее, K(τ) = s²δ(τ) , где δ(τ) – функция Дирака.

Модель авторегрессии – скользящего среднего (АРСС или ARMA, английское – Auto Regression - Moving Average) имеет вид

          x_t+a₁x_t-1+a₂x_t-2 + ….+ a_m x_t-m = ξ_t +b₁ξ _t-1+…+b_n ξ_t-n ,                                                               (10.1)

числа m  и n определяют порядок модели ARMA (m, n). Равенство (10.1) можно записать короче, используя оператор сдвига по времени

Q x_t = x_t-1,  Q^s x_t = x_t-s

и операторы-многочлены в (10.1)

a( Q) = 1+a₁Q+ a₂Q²+…+ a_mQ^m

b( Q) = 1+b₁Q+ b₂Q²+…+b_nQⁿ

В этих обозначениях модель (10.1) запишется в виде

    

                                                          a( Q) x_t = b( Q) ξ_t .                                                                    (10.2) 

 

          Рассмотрим важные частные случаи. Модель AR(1) авторегрессии I порядка имеет вид

x_t+ a₁x_t-1 = ξ_t .                                                        (10.3)

   Этой дискретной статистической модели соответствует дифференциальное уравнение I порядка в шкале непрерывного времени

.

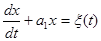   Модель AR(2) авторегрессии II порядка имеет вид 

 x_t+ a₁x_t-1+ a₂x_t-2= ξ_t .                                                   (10.4)

  Её аналогом в непрерывной шкале будет дифференциальное уравнение II порядка

.

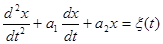  Можно показать, что процесс x_t , вычисляемый по дискретной модели (10.3), (10.4), будет стационарным при условии, что корни функций комплексного переменного z= x+ iy, составленных по правилам φ₁(z) = 1+a₁z для AR(1) и φ₂(z) = 1+a₁z + a₂z² для AR(2), удовлетворяют условию |z| > 1 .

После замены z = 1/ζ получим уравнения     

ζ+a₁ = 0;  ζ²+b₁ζ+b₂ = 0,

корни которых должны лежать внутри круга единичного радиуса |ζ|<1 (иначе процесс не будет стационарным).

   В общем случае модели ARMA (m, n) условие стационарности |z| > 1 должно выполняться для корней функции

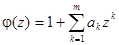
При изучении нестационарных временных рядов часто используется более общая модель ARIMA( m, d, n) – модель авторегрессии–проинтегрированного скользящего среднего, в русской аббревиатуре - АРПСС. По сравнению с ранее обсуждавшимися моделями модель ARIMA предполагает d– кратное применение оператора конечных разностей

                        x_t = y_t - y_t-1 = (1-Q) y_t                                                  (10.5)

к исходному временному ряду. Операция (10.5) устраняет линейный тренд. Действительно, если y_t=а+bt, то y_t-1=а+b(t-1) и x_t= b. Повторяя эту операцию несколько раз, можно получить (с некоторым приближением) стационарный временной ряд, который описывает модель ARMA. При восстановлении исходного ряда производится суммирование его членов, что соответствует интегрированию в непрерывном времени. Последнее обстоятельство проясняет смысл названия модели ARIMA.

Учет сезонных составляющих

 

Обобщение модели ARIMA, позволяющие учесть периодические (сезонные) составляющие временного ряда было предложено Дж. Боксом и Г. Дженкинсом [2]. Этот метод реализован в системе статистической обработки данных STATISTICA, поэтому мы коротко его опишем.

Пусть ряд x_t  имеет период S , так, что x_t =  x_{t- s} . Модель Бокса-Дженкинса имеет вид     

                               A( Q^S) Ñ ^D _S x_t = B( Q^S)ζ_t                                                (11.1)

                                  a(Q) Ñ ^d x_t = b(Q) x _t ,                                             (11.2)

 где Q^Sx_t = x_t-s , Ñ _S x_t = x_t -  x_t-s = (1- Q^S )x_t ,

A(Q)= 1+A₁ Q+A₂ Q²+…A_M Q^M

B(Q)= 1+B₁ Q+B₂ Q²+…B_N Q^N

  Из формул (11.1), (11.2) видно, что модели характеризуются двумя тройками чисел (M,D, N) и (m, d, n). Ряд ζ_t введен для удобства, в принципе его можно исключить. Например, пусть M = m = 0, N = n = 1,     D = d = 1, S = 12. Модель (11.1), (11.2) примет вид   

Ñ₁₂x_t= ζ_t + B₁ζ_t-12

Ñζ_t = x _t+ b₁x _t-1                                                                     (11.3)

Но Ñ ₁₂ x_t = x_t- x_t-12, Ñ ζ_t = ζ_t -ζ_{t -1} Поэтому  

 

                                                  x_t- x_t-12 = ζ_t + B₁ζ_t-12                                                                 (11.4)

                                                 x_t-1- x_t-13 = ζ_{t -1}+ B₁ζ_t-13                                                                    (11.5)

 Теперь вычтем (11.5) из равенства (11.4):    

x_t- x_t-12- x_t-1+ x_t-13 = ζ_t - ζ_{t -1} + B₁(ζt_-12- ζ_{t -13}).

 Используя формулу (11.3), получим окончательно

x_t- x_t-12- x_t-1+ x_t-13 = x _t +b₁x _t-1+ B₁(x _t-12+ b₁ x _t-13).

Коэффициенты b₁, B₁ можно подобрать по данным x_t . В примере, приведенном в книге [2], оказалось, что b₁ = -0,4; B₁ = - 0,6.

 

 

 

 

---

Дата добавления: 2018-10-26; просмотров: 216; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!