Парная линейная регрессия. Метод наименьших квадратов

 

Пусть имеется n пар чисел (x_i, y_i), i=1,2,…, n, относительно которых предполагается, что они отвечают линейной зависимости между величинами x и y:

                                             y= a+ bx,                                                           (3.1)

возможно, с некоторой ошибкой e _i, так что

                                     y_i= a+ bx_i+ e _i,   i=1,2,…, n .                         (3.2)

Какими должны быть наилучшие значения параметров a и b?   

Применяя метод наименьших квадратов, мы требуем, чтобы сумма квадратов ошибок e _i была наименьшей:    

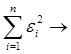min.                                                    (3.3)

 Подставляя значения e _i из (3.2) в (3.3), получим функцию

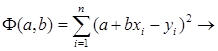                                                 min.

Необходимым условием минимума этой функции, как известно, является равенство нулю ее частных производных по a и b:
                                                , .
 Вычисляя производные, приходим к системе уравнений

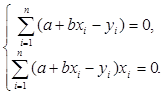                                                                                                   (3.4)

Заметим, что уравнения (3.4) можно записать короче в виде

                                                                                                                     (3.5)

Если раскрыть скобки в уравнениях (3.4), то после простых преобразований
получим систему

                                                        (3.6)
 решение которой находится без большого труда:

                              ,                                    (3.7)

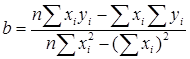                        .                                               (3.8)

Введем обозначения:

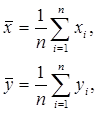                                                                                                  (3.9)

                        ,                              (3.10)

                        .             (3.11)

В курсах математической статистики величины 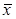,  называются выборочными средними, ­­­­­­­­ – выборочной дисперсией,  – выборочной ковариацией. Теперь формулу (3.8) можно переписать в виде

,                                                            (3.12)

 а выражение для a получается из первого уравнения (3.6):

                                        .                                                       (3.13)

Из формулы (3.13) видно, что точка  лежит на прямой y= a+ bx (при найденных значениях a и b). Поэтому функцию (3.1) можно записать также в виде , где параметр b определяется по формуле (3.12).

   Предположим теперь, что зависимость y от x не является линейной и выражается формулой

                        y_i = a+bf(x_i)+e_i , i =1,2,…,n .                                   (3.14)

 

Введем обозначения

; , , ,

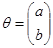где n – число измеренных значений фактора x, а F_i = f( x_i).

В матричной форме система уравнений (3.14) принимает стандартный вид

                                                              Y = F q+e.                                                              (3.15)

Для определения параметров a и b, объединенных в вектор q , можно применить метод наименьших квадратов (отметим, что относительно искомых параметров формула (3.14) осталась линейной). В следующем параграфе показано, что решение этой задачи имеет вид

                                  q = ( F^TF)^-1 F^TY.                                                         (3.16)

 

Множественная линейная регрессия

 

Парная регрессия может дать хороший результат при моделировании, если влиянием других факторов, воздействующих на объект исследования, можно пренебречь. Но, существует обычно несколько факторов, которые оказывают существенное влияние (например: на потребление того или иного товара влияют такие факторы, как цена товара, размер семьи, её состав, доход и т.д.). В этом случае следует попытаться выявить влияние этих факторов, введя их в модель, т.е. построить уравнение множественной регрессии.

Включение в уравнение множественной регрессии того или иного набора факторов связано прежде всего с представлением о природе взаимосвязи моделируемого показателя с другими экономическими явлениями. Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:

· Факторы должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность. Например, если анализируется спрос на мороженое летом и зимой, то фактор сезонности можно учесть бинарной переменной, принимающей значения 1 и 0. Аналогичным образом учитывается наличие балкона, этаж, тип здания (кирпичный или блочный дом) на рынке недвижимости и т. п.

· Факторы не должны быть коррелированы и тем более находиться в точной функциональной связи.

В случае учета влияния нескольких факторов линейная зависимость величины y от
m переменных x₁, x₂,…, x_m  примет вид:

                         y =q₁x₁+q₂x₂+…+q_m x_m .                                                      (4.1)

Конкретные значения независимых переменных будем отмечать двумя индексами:    x_i1, x_i2,…, x_im, (i = 1,2,…, n). Тогда можно записать уравнения

                                          ,                                                          (4.2)

где m – число рассматриваемых факторов.

Зависимость (4.2) будем называть множественной линейной регрессией.

Если зависимость величины y  от переменных x₁, x₂,…, x_m  имеет вид

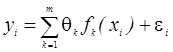, i=1,2,…,n                                         (4.3)

то, введя обозначение F_ik= f_k( x_i), запишем формулу (4.3) в виде

                                  .                                                                 (4.4)

В качестве примеров зависимости типа (4.3) отметим квадратичную функцию y= a+ bx+ cx² , полином третьей степени y= a+ bx+ cx² + dx³ , тригонометрический полином y= q ₁ sinx + q₂ sin2 x+…+ q _m sin mx и др.

Сравнив формулы (4.2) и (4.4), нетрудно убедиться в том, что они отличаются только обозначениями заданных коэффициентов F_ik и x_ik. В матричном виде имеем формулу

 

        y= Fq+e ,                                                                                (4.5)

 где

           , ,      .

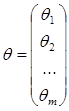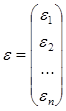
 Для определения коэффициентов q _k в формулах (4.2) или (4.4) воспользуемся методом наименьших квадратов:

                       min .

Необходимое условие экстремума функции F= F (q₁,q₂,…,q_т)  

, p=1,2,…, m

дает уравнение

                                                                     (4.6)

В уравнении (4.6) переставим порядок суммирования :

                                                                        (4.7)

В матричной форме система уравнений (4.7) относительно неизвестных значений переменной q _k имеет вид

            F^TFq = F^Ty .                                                    (4.8)

Полагая, что матрица F^TF неособенная, получим решение системы (4.8)

          q = ( F^TF)^-1 F^Ty .                                                (4.9)

В случае парной регрессии (3.1) вектор параметров q имеет вид

;

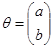переменную x₁ следует принять равной 1, а переменную x₂= x; тогда матрица F принимает вид

.

 Произведение матриц

представляет собой матрицу коэффициентов системы (3.6), а свободный член в формуле (4.8)

совпадает со свободными членами уравнений (3.6).

Точно также в случае множественной линейной регрессии для уравнения y= q₀+ q₁ x₁+ q₂ x₂ первый столбец матрицы F состоит из 1, второй столбец - из заданных значений переменной x₁, а третий – из значений x₂:

;

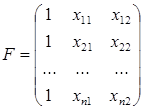Вектор параметров принимает вид

.

 

§5. Нелинейные модели

 

Мы изучили применение метода наименьших квадратов для определения параметров, которые входят в функциональные зависимости линейно. Поэтому для них в параграфах 3 и 4 получились системы линейных уравнений (3.6), (4.8). Однако в эконометрике приходится иметь дело и с такими функциональными зависимостями, неизвестные параметры которых входят в эти зависимости нелинейно. Например, параметр a в зависимостях       

y= ax ^a ,                                                           (5.1)

                                                y= ae ^{a x}                                                            (5.2)

в случае двух величин (x, y), параметры a₁, a₂, …, a _m в зависимости    

                                                                                             (5.3)

 и др. Типичным примером является функция Кобба – Дугласа y= aL ^a K^b, где a>0, 0< a<1, 0<b <1, обычно принимают также условие a+b =1. Эта функция выражает зависимость произведенной продукции y от объема привлеченных трудовых ресурсов (числом рабочих, человеко-часов и т.п.) L и объема основных фондов K.

При определении параметров в формуле (5.1), (5.2) или параметров a₁, a₂, …, a _m в формуле (5.3) методом наименьших квадратов их следует предварительно прологарифмировать. Например, логарифмирование степенной функции y= ax ^a  дает уравнение

ln y= ln a+a ln x,

линейное относительно величин A= ln a и a. Сделав замену переменных: Y= ln y,

A= ln a, X= ln x, получим соотношение Y= A+ a X, определение параметров которого по методу наименьших квадратов приведет к системе линейных уравнений. Линеаризация формулы (5.3) также достигается логарифмированием:

ln y= ln a+ a₁ ln x₁+ a₂ ln x₂+…+ a _m ln x_m,

Замена переменных: Y= ln y, A= ln a, X_i= lg x_i приводит к модели линейной множественной регрессии

Y= A+ a₁ X₁+ a₂ X₂+…+ a _m X_m.

Есть модели, которые не могут быть приведены к линейному по коэффициентам виду. Например: . Для оценки параметров таких моделей используются итеративные процедуры, успешность которых зависит от вида уравнений и особенностей применяемого итеративного подхода. Однако гораздо большее распространение получили модели, приводимые к линейному виду. Оценка параметров такого типа моделей реализовано в стандартных пакетах прикладных программ EXCEL, STATISTICA и др.

Таким образом, если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью нелинейных функций. Различают два класса нелинейных моделей:

· модели, нелинейные относительно включенных в анализ объясняющих
   переменных, но линейные по оцениваемым параметрам;

· модели, нелинейные по оцениваемым параметрам.

Примерами нелинейных моделей первого класса могут служить следующие функции:

· полиномы разных степеней: y = a₀+ a₁ x+ a₂ x²+…+ a_nxⁿ;

· гиперболическая зависимость:

· тригонометрические полиномы y= a₁ sin x +b₁cos x + a₂ sin 2x +b₂ cos2 x+…
   + a_m sin mx +b_mcos mx.

К нелинейным моделям второго класса относятся функции:

· степенная: y = ax^b ;

· показательная: y = ab^x ;

· экспоненциальная: .

 

---

Дата добавления: 2018-10-26; просмотров: 405; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!