Значения относительных важностей

⇐ ПредыдущаяСтр 10 из 18Следующая ⇒

Музыкальный жанр	Вес
Музыкальный жанр	#1	#2	#3
Рок	0,185	0,183	0,173
Поп	0,162	0,13	0,131
Народная	0,077	0,119	0,093
Джаз	0,114	0,131	0,117
Кино	0,196	0,163	0,18
Эстрада	0,118	0,121	0,124
Классика	0,149	0,152	0,182

Веса факторов, полученные в результате проведенных экспериментов, сравним с результатами опроса, проведенного в Internet и представленными в таблице 6.

Таблица 6.

Результаты опроса, проведенного в Internet .

Музыкальный жанр	% людей	Кол-во предпочтений	Вес
Поп	31,02	134	0,31
Рок	29,86	129	0,299
Эстрадная	12,04	52	0,12
Джаз	9,72	42	0,097
Классика	7,18	31	0,072
Кино	5,79	25	0,058
Народная	4,4	19	0,044

Теперь сведем в таблицу 7 результаты проведенных экспериментальных экспертных опросов .

Таблица 7.

Результаты экспериментальных экспертных опросов

Музыкальный жанр	#1		#2		#3
Музыкальный жанр	Частота	%	Частота	%	Частота	%
Поп	8	10,96	8	10,96	9	12,53
Рок	22	30,14	36	49,32	2	30,14
Эстрадная	6	8,22	8	10,96	5	6,85
Джаз	13	17,81	10	13,69	8	10,96
Классика	5	6,85	8	10,96	17	23,29
Кино	10	13,69	11	15,07	14	19,18
Народная	1	1,37	2	2,74	5	6,85

Каждый стимул (музыкальный жанр) можно представить точкой в некотором координатном пространстве, величины проекций этих точек на оси соответствуют значению фактора, характеризующего данный стимул. Чем больше величина проекций, тем большим значением фактора обладает стимул. Мера сходства между двумя стимулами обратна расстоянию между соответствующими им точками. Чем ближе стимулы друг к другу, тем выше мера сходства между ними (и ниже мера различия), далеким точкам соответствует низкая мера сходства. Чтобы точным образом измерить близости, необходимо ввести метрику в искомом координатном пространстве. Для этого воспользуемся двумя наиболее распространенными метриками - метрикой Минковского и Евклидовой метрикой в качестве меры сходства между элементами множества результатов Internet-опроса и результатами каждого из исследованных в экспериментальной процедуре методов измерения. Полученные результаты приведены в таблице 8.

Таблица 8.

Мера близости к эталонной выборке

Метрика	№1	№2	№3
Минковского	0,727	0,769	0,78
Евклидова	0,247	0,265	0,279

Полученные результаты свидетельствуют о том, что в случае эксперимента №3, когда испытуемые назначали веса в числовых градациях, оценки больше различаются от оценок Internet-опроса. В случае №1, когда испытуемым предлагался метод парных сравнений - наиболее близки к эталонным результатам. То есть, метод парных сравнений позволяет получить более точные результаты, но требует гораздо больше времени от экспериментатора на подготовку стимульного материала, а от испытуемого - на ответы.

Метод назначения весов в числовых градациях дает наименее точные результаты, и метод получения результатов в словесных градациях качества, являясь наиболее интуитивно ясным, позволяет получать достаточно адекватные оценки.

Аксиоматические методы

Иногда их рассматривают даже как единственный "научно обоснованный" подход (многокритериальная теория полезности). Опирается данная модель на теорию ожидаемой полезности фон Неймана и Моргенштерна. Аксиоматические методы подходят к измерению ценности, полезности альтернатив как последовательности определенных шагов, подтверждающих справедливость выбора некоторых аксиом, на основании которых обосновывается возможность использования функции полезности определенного вида.

Аксиоматические методы подразделяются на две группы:

- принятие решений при определенности (оценки альтернатив считаются известными)

- принятие решений при риске (заданы функции распределения вероятностей оценок альтернатив).

Обе группы методов используют близкую систему аксиом (три группы):

1. Аксиомы "слабого порядка" и транзитивности.

В условиях определенности.

Пусть u,v,w U - полезности альтернатив.

Тогда:

а) для любых u,v имеет место одно из следующих соотношений:

u = v, u > v, u < v

б) из u > v, v > w следует u > w

В условиях риска:

Пусть R - множество распределений вероятностей на множестве альтернатив. Каждое распределение P в R можно представить в виде лотереи

L = (p₁₍a₁₎, p₂₍a₂₎, ..., p_r₍a_r₎), где p₁, p₂,..., p_r – вероятности осуществления альтернатив a₁, a₂,..., a_r

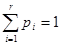
Каждому распределению P или Q в R можно приписать определенное числовое значение ожидаемой полезности U(P) или U(Q) такое, что P < Q, тогда и только тогда, когда U(P) < U(Q)

Тогда для распределений P,Q,W:

а) имеет место одно из соотношений:

U(P) > U(Q), U(P) < U(Q), U(P) = U(Q)

б) если U(P) > U(Q), U(Q) > U(W), то U(P) > U(W)

2. Аксиомы, исключающие ненормальности в предпочтениях.

а) Возможности использования любых частей полезности 2-х альтернатив для выражения эквивалентной полезности третьей (аксиома растворимости):

Для детерминированного случая:

из u > w > v следует, что существует такое a, 0 < a < 1, что

au + (1 - a)v = w

Для условий риска:

если U(P) > U(Q) > U(W), то существует такое a, 0 < a < 1, что

aU(P) + (1-a)U(W) = U(Q)

б) Запрещение использования альтернатив, неизмеримо превосходящих другие (Архимедова аксиома):

Для детерминированного случая:

если w > v > u, то существует такое a, 0 < a < 1, что

v > au + (1 - a)w

Для условий риска:

если U(P) < U(Q) < U(W), то существуют такие p,q, 0 < p,q < 1,

что:

pU(P) + (1-p)U(W) < U(Q),

U(Q) < qU(P) + (1-q)U(W)

3. Аксиомы независимости. Эти аксиомы выражают требования, чтобы предпочтения между альтернативами не зависели от некоторых преобразований этих альтернатив. Чаще всего используются:

Для детерминированного случая:

а) Слабая условная независимость по полезности:

предпочтения для двух альтернатив, отличающихся лишь оценками по шкале одного критерия, не зависят от оценок этих альтернатив по шкалам других критериев

б) Совместная независимость:

предпочтения между альтернативами, отличающимися оценками по определенному подмножеству критериев, не зависят от одинаковых оценок по критериям оставшегося подмножества

Для условий риска:

в) Аксиома эквивалента определенности:

предпочтения между лотереями не должны зависеть от одинаковых составляющих исходов лотерей

г) Аксиома строгой условной независимости по полезности:

предпочтения среди многокритериальных альтернатив, для которых часть оценок по критериям задана распределением вероятностей,

а другая часть имеет постоянные значения, не зависят от этих постоянных значений

д) Аксиома маргинальности:

многокритериальные альтернативы сравнимы между собой только на основе рассмотрения распределений вероятностей оценок по отдельным критериям

Использование аксиом

Рассмотренные выше аксиомы обычно используются для доказательства существования функции полезности определенного вида.

Можно доказать, что при справедливости аксиом групп 1 и 2 (слабого порядка и транзитивности, исключения ненормальностей в предпочтениях), а также условной независимости и совместной независимости функция полезности может быть выражена в виде:

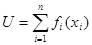
где

x_i – оценка альтернативы по i-му критерию, f_i – частная функция полезности по i-му критерию.

При выполнении аксиом определенного эквивалента, строгой условной независимости, маргинальности полезности для случая риска полезность альтернативы может быть выражена

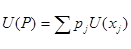
где

p_j – вероятность осуществления j-й альтернативы, x_j - вектор многокритериальных оценок j-й альтернативы.

Достаточно часто формулируются другие аксиомы независимости с целью доказать существование функции полезности определенного конкретного вида.

Пример. Изучалась проблема выбора энергетической политики для штата Висконсин. В качестве критериев оценки рассматривались: выработка электроэнергии, количество земли под электростанцию, наличие радиоактивных отходов и т.п. - всего 11 критериев. Были определены верхняя и нижняя оценки на количественных шкалах оценок критериев.

При проверке независимости по предпочтению Р.Кини спрашивал ЛПР, например, какому количеству радиоактивных отходов эквивалентны 2000 акров земли, занятой под электростанцию, при лучших оценках по остальным 9 критериям. Далее этот вопрос повторялся при худших оценках по остальным 9 критериям. В случае одинакового ответа делался вывод о независимости по предпочтениям этих двух критериев.

Проверка независимости по полезности проводилась следующим образом. От ЛПР требовался эквивалент определенности для лотереи, дающей с вероятностью 0,5 либо 200 т радиоактивных отходов либо их отсутствие при лучших оценках по прочим 10 критериям. Далее повторялся тот же вопрос при худших оценках по прочим 10 критериям. При одинаковых ответах делался вывод о независимости по полезности.

Далее рассматривалась задача нахождения весовых коэффициентов важности критериев. Первоначально критерии упорядочивались по важности, при этом от ЛПР требовалось сравнение по важности перехода от худших к лучшим оценкам для двух критериев. Затем критерии рассматривались попарно, и ЛПР находил две точки безразличия:

первую - с лучшей оценкой по более важному критерию и худшей по менее важному и

вторую - с лучшей оценкой по менее важному критерию и промежуточной по более важному.

Так, например, определялось, что альтернатива с 0.5 млрд. квт-час электроэнергии (минимальное значение) при отсутствии радиоактивных отходов эквивалентна для ЛПР альтернативе с 3 млрд. квт-час (максимальное значение) при определенном количестве радиоактивных отходов. На основании пар безразличия была составлена система линейных уравнений, решение которых дало согласованные веса критериев. Сумма этих весов оказалась близкой к единице,

что позволило использовать аддитивное представление функции полезности:

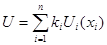при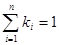

Построение кривых полезности по отдельным критериям осуществлялось при помощи сравнения лотерей. Лучшей оценке присваивалась полезность U = 1, худшей - U = 0. От ЛПР требовался эквивалент определенности для лотереи, дающей с вероятностью 0.5 лучшую и с вероятностью 0.5 худшую оценки. Далее находились эквиваленты определенности для лотерей, включающих найденное значение из первой лотереи и одно из крайних, и т.д. Зная оценки альтернатив, кривые полезности для отдельных критериев и весовые коэффициенты, можно подсчитать по формуле взвешенной суммы оценки полезности любой из альтернатив.

Обычно, справедливость аксиом первой группы не оспаривается. По второй группе - справедливость аксиом не всегда наблюдается, особенно при дискретных шкалах. Подлинный камень преткновения - аксиомы о независимости. Трудно с аксиомами сравнимости лотерей. Они часто выглядят искусственными и час-

то противоречат реально применяемым ЛПР алгоритмам.

Следует также отметить искусственность аксиоматических методов и проблема сравнения альтернатив отступает перед проблемой поиска функции полезности в определенной форме. На практике находят применение элементы аксиоматических методов.

Прямые методы

В этих методах форма зависимости результирующей (глобальной) полезности альтернатив от их оценок по множеству критериев задается без всяких теоретических оснований - как правило на основе некоторых основополагающих предположений, а параметры зависимости напрямую оцениваются ЛПР.

Прямые методы можно разделить на пять групп:

1) постулируется как сама основная формула полезности для многокритериальной альтернативы, так и все ее параметры. Для этого обычно используются некоторые принципы (например, одинаковой степени достижения экстремума по всем критериям)

2) ЛПР выбирает один из способов определения полезности альтернатив при неизвестной информации о вероятности различных внешних условий

3) двойники аксиоматических методов: постулируется основная форма зависимости, но ее параметры непосредственно назначаются ЛПР. Например - метод взвешенных сумм

4) основная форма зависимости задается, а ее параметры определяются путем вычислений, проводимых на основе прямой оценки ЛПР полезностей некоторых многокритериальных альтернатив

5) за основу берется формула максимизации ожидаемой полезности (которая постулируется), а ЛПР определяет вероятностные оценки различных исходов на деревьях решений

Рассмотрим эти методы более подробно.

Постулируемые принципы

Этот подход внешне выглядит самым простым: ЛПР предлагается ряд принципов, принятие каждого из которых влечет выбор определенной зависимости между полезностью многокритериальной альтернативы и ее оценками по критериям. Например, глобальная функция полезности может иметь вид:

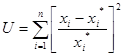
где x_i* - наилучшая оценка по критерию q_i, x_i- фактическая оценка по i-му критерию.

При такой зависимости для всех критериев как бы вводится квадратичный штраф за отклонения от наилучшего значения. Данный подход пригоден прежде всего для динамических систем, где оптимизация по каждому отдельному критерию достаточно трудоемка, а время принятия решения ограничено.

Выбор глобального критерия

Для методов данной группы исходной информацией является следующая таблица:

Альтернативы	Варианты внешних условий
Альтернативы	B₁	B₂	…	B_m
a₁ a₂ … a_n	U₁₁ U₂₁ U_n1	U₁₂ U₂₂ U_n2		U_1m U_2m U_nm

Выбор предпочтительной альтернативы(с полезностью U* ) производится на основании одного из следующих критериев:

1) Максиминный критерий (наибольшая осторожность). Оптимальное решение выбирается как:

U* = max min U_ij

i j

где i - индекс строки, j - индекс столбца таблицы

2) Критерий минимаксного сожаления.

Вводится понятие сожаления для i-й альтернативы при j-м варианте внешних условий:

c_ij = max U_ij - U_ij

далее выбирается

U* = min c_ij

3) Критерий максимакса (крайний оптимизм):

U* = max max U_ij

i j

4) Критерий Гурвича.

Пусть для i-й альтернативы имеются оценки:

m_i = min U_ij, M_i = max U_ij

j j

Для каждой альтернативы a_i определяется некоторая взвешенная полезность :

U_i(q) = qm_i + (1-q)M_i, где 0< q <1

Далее при заданном значении q определяется оптимальное значение альтернативы как

U* = max U_i(q)

Можно говорить, что величина q задает уровень оптимизма: при q=1 получаем случай максмина (1), а при q=0 – максмакса (3).

5) Критерий Лапласа.

Все варианты внешних условий принимаются равновероятными и для

каждой альтернативы a_i определяется показатель

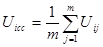
и оптимальное решение определяется на основании:

U* = max U_i_ср

Дата добавления: 2018-09-23; просмотров: 237; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 5 6 7 8 91011 12 13 14 Следующая ⇒

Мы поможем в написании ваших работ!