Нормальний, рівномірний та показниковий закони
Розподілу ймовірностей.
Нормальним називається розподіл імовірностей неперервної випадкової величини, диференціальна функція якої має вигляд: 
, де параметр 
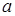– математичне сподівання, параметр 
– середнє квадратичне відхилення. Графік щільності ймовірності нормального розподілу називають нормальною кривою (кривою Гаусса):
Рис. 8.5.1 – Крива Гаусса
Імовірність того, що нормальна випадкова величина 
прийме значення з інтервалу 
:
, (8.5.1)
де 
– функція Лапласа (табульована у додатку Б).
Імовірність того, що відхилення нормально розподіленої випадкової величини від її математичного сподівання 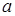за абсолютною величиною менше заданого додатного числа 
:
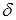(8.5.2)
Правило “трьох сигм” Практично достовірною є подія, що полягає у тому, що абсолютна величина відхилення нормально розподіленої випадкової величини від її математичного сподівання не перевищує потроєного середнього квадратичного відхилення:
(8.5.3)
Нормальний закон проявляється в усіх тих випадках, коли випадкова величина є результатом дії великого числа різних факторів. Прикладами випадкових величин, що мають нормальний розподіл, можуть бути: відхилення від номінальних розмірів деталей, оброблених на станку, помилки при вимірюваннях, відхилення від цілі при стрільбі і т.д.
Приклад 8.5.1. Вага виробу має нормальний закон з 
г і 
г. Знайти ймовірності того, що: а) вага виробу не менша 2990 г і не більша 3005 г; б) вага виробу відхиляється від середнього значення 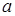не більше ніж на 15 г.
|
|
|
Розв’язання. Випадкова величина – вага виробу є нормально розподіленою, тому маємо:
а) за формулою (8.5.1) ( 
, 
):
.
За таблицею (додаток Б) знаходимо: 
, 
, значить, 
.
б) при 
г за формулою (8.5.2):
.
Рівномірним називається розподіл імовірностей неперервної випадкової величини, всі значення якої належать відрізку 
, а диференціальна функція зберігає стале значення на 
. Диференціальна та інтегральна функції рівномірного розподілу мають вигляд:
. (8.5.4)
Графіки цих функцій:
Рис. 8.5.2 – Диференціальна функція рівномірного розподілу
Рис. 8.5.3 –Інтегральна функція рівномірного розподілу
Числові характеристики (математичне сподівання, дисперсія):
, 
. (8.5.5)
Приклад 8.5.2. Потяги метрополітена йдуть строго за розкладом з інтервалом 2 хвилини. Час очікування потягу (пасажиром, який вийшов на платформу) є рівномірно розподіленою випадковою величиною . Знайти: а) диференціальну та інтегральну функції; б)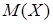 
, 
, 
.
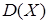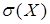Розв’язання. Випадкова величина – час очікування потягу – рівномірно розподілена на відрізку [0; 2]. Таким чином, у даному випадку 
, 
.
|
|
|
а) Диференціальна та інтегральна функції цього рівномірного розподілу згідно (8.5.4) мають вигляд:
, 
.
б) математичне сподівання, дисперсія та середнє квадратичне відхилення за формулами (8.5.5): 
, 
, та (8.2.14): 
.
Показниковий розподіл неперервної випадкової величини описується диференціальною та інтегральною функціями:
(8.5.6)
де параметр розподілу 
.
Числові характеристики:
, 
. (8.5.7)
Імовірність попадання в інтервал 
:
. (8.5.8)
Нехай 
– кількість годин, які пропрацював прилад до першої поломки. Функція розподілу випадкової величини , тобто 
визначає ймовірність відмови протягом часу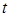 
. Тоді ймовірність безвідмовної роботи 
. Функція 
називається функцією надійності. Випадкова величина часто має показниковий розподіл, тобто 
, тоді 
, де 
– інтенсивність відмов, тобто середнє число відмов за одиницю часу.
Приклад 8.5.3. Середня тривалість роботи приладу до першої поломки 100 годин. Випадкова величина – години роботи приладу – має показниковий розподіл. Знайти: а) 
, 
, 
; б) ймовірність того, що прилад пропрацює від 40 до 190 годин; в) ймовірность того, що прилад пропрацює менше 50 годин.
|
|
|
Розв’язання. а) За умовою задачі маємо 
(годин), отже згідно (8.5.7) 
, тобто 
. Значить, за формулами (8.5.7): 
, та (8.2.6): 
.
б) Ймовірність того, що прилад пропрацює від 40 до 190 годин за формулою (8.5.8):
.
в) Ймовірність, що прилад пропрацює менше 50 годин згідно (8.5.8): 
.
Зауважимо, що приклад 8.5.1 відповідає завданню 8.5 контрольної роботи.
Література: [1, с. 530 ‑ 535], [4, с. 565 – 575], [16], [18], [20].
Дата добавления: 2018-09-22; просмотров: 313; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!