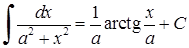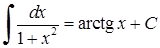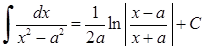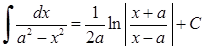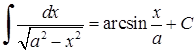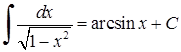НЕВИЗНАЧЕНИЙ І ВИЗНАЧЕНИЙ ІНТЕГРАЛИ
Основні методи інтегрування
Інтегрування є зворотною задачею диференціювання. Функція  називається первісною для функції
називається первісною для функції 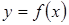 на інтервалі
на інтервалі 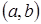 , якщо для будь-якого
, якщо для будь-якого 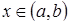 виконується рівність
виконується рівність 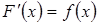 . Множина всіх первіснихфункції
. Множина всіх первіснихфункції 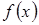 називається невизначеним інтегралом:
називається невизначеним інтегралом: 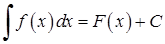 , де
, де  ‑ довільна стала.
‑ довільна стала.
Таблиця основних і нтеграл і в :
1) 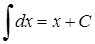
| 1 0) 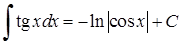
|
2) 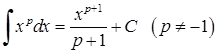
| 1 1) 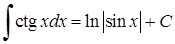
|
3) 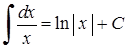
| 1 2) |
4) 
| |
5) 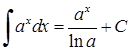 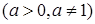
| 1 3) |
6) 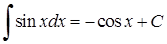
| |
7) 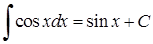
| 1 4) |
8) 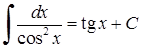
| |
9) 
| 1 5) 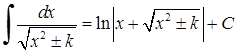
|
Основні властивості невизначеного та
визначеного інтеграл і в:
· 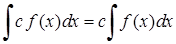 ,
, 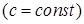 (3.1.1)
(3.1.1)
· 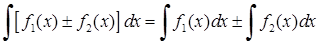 , (3.1.2)
, (3.1.2)
· 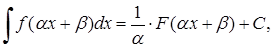 (3.1.3)
(3.1.3)
якщо 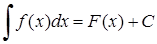 ,
, 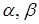 ‑ сталі;
‑ сталі;
·  , (3.1.4)
, (3.1.4)
· інваріантність формул інтегрування:
якщо 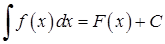 , то
, то 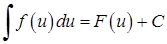 , (3.1.5)
, (3.1.5)
де 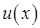 – довільна диференційована функція;
– довільна диференційована функція;
· 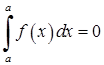 ,
,  ; (3.1.6)
; (3.1.6)
·  (де
(де  ). (3.1.7)
). (3.1.7)
Для обчислення визначених інтегралів спочатку знаходять невизначений інтеграл (або первісну), а потім користуються формулою Ньютона-Лейбніца:
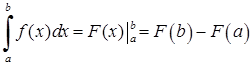 , (3.1.8)
, (3.1.8)
де 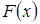 ‑ первісна для неперервної функції
‑ первісна для неперервної функції 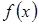 .
.
Метод безпосереднього інтегрування базується на прямому використанні основних властивостей невизначеного інтеграла та проведенні тотожних перетворень підінтегральної функції з метою одержання табличних інтегралів або їх суми.
|
|
|
Метод заміни змінної (підстановки) застосовується, коли в підінтегральному виразі є функція 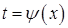 й її диференціал
й її диференціал 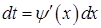 :
:
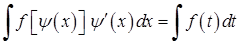 , (3.1.9)
, (3.1.9)
де 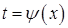 – нова змінна,
– нова змінна, 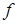 ,
, 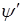 неперервні функції.
неперервні функції.
Користуючись формулою заміни у визначеному інтегралі, на відміну від невизначеного, не треба повертатись до попередньої змінної.
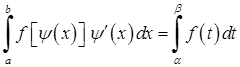 , (3.1.10)
, (3.1.10)
де 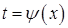 – нова змінна,
– нова змінна, 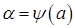 і
і  – нові межі інтегрування,
– нові межі інтегрування, 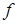 неперервна на відрізку
неперервна на відрізку 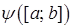 ,
, 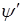 неперервна на
неперервна на 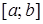 .
.
В формулах інтегрування частинами
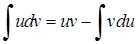 , (3.1.11)
, (3.1.11)
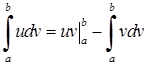 (3.1.12)
(3.1.12)
(де 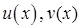 мають неперервну похідну) ліва частина є компактним записом шуканого інтеграла, а права – шляху його відшукання.
мають неперервну похідну) ліва частина є компактним записом шуканого інтеграла, а права – шляху його відшукання.
Щоб обчислити інтеграли 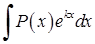 ,
, 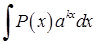 ,
,  ,
, 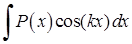 в якості
в якості 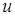 доцільно позначати многочлен
доцільно позначати многочлен 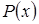 , а
, а 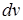 - вирази -
- вирази - 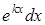 ,
, 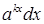 ,
, 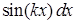 ,
, 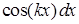 .
.
Щоб знайти інтеграли 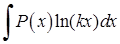 ,
, 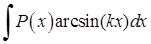 ,
, 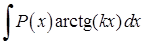 в якості
в якості 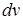 береться
береться  , а
, а 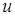 - функції
- функції 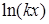 ,
,  ,
, 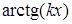 .
.
За необхідності інтегрування частинами проводиться кілька разів. Наприклад, для інтеграла  дворазове інтегрування частинами (зі збереженням вибору
дворазове інтегрування частинами (зі збереженням вибору 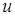 ) призводить до повернення до шуканого інтеграла (і дозволяє таким чином його виразити).
) призводить до повернення до шуканого інтеграла (і дозволяє таким чином його виразити).
|
|
|
Інтегрування добутків тригонометричних функцій  ,
,  ,
, 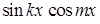 (де
(де  – числа) здійснюється шляхом попереднього їх перетворення в алгебраїчні суми за допомогою формул:
– числа) здійснюється шляхом попереднього їх перетворення в алгебраїчні суми за допомогою формул:
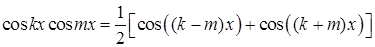 ;
; 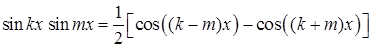 ;
; 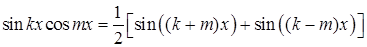 .
.
Приклад 3.1.1. Знайти методом безпосереднього інтегрування невизначені та визначені інтеграли: 1) 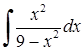 , 2)
, 2) 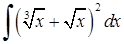 , 3)
, 3) 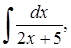
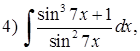

Розв’язання. 1) Для обчислення інтеграла 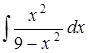 віднімемо і додамо в чисельнику число 9 та застосуємо властивості (3.1.1), (3.1.2) та табличні інтеграли 1) та 13)
віднімемо і додамо в чисельнику число 9 та застосуємо властивості (3.1.1), (3.1.2) та табличні інтеграли 1) та 13) 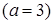 :
:
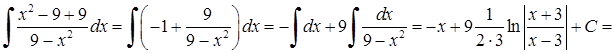
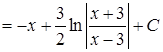 .
.
2) Підносячи вираз в дужках до другого степеня, а потім інтегруючи кожний доданок, згідно (3.1.2) маємо:
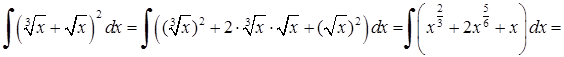
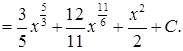
Зауважимо, що 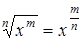 ,
, 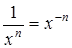 , тому інтеграли від цих функцій обчислюються за формулою 2) таблиці інтегралів.
, тому інтеграли від цих функцій обчислюються за формулою 2) таблиці інтегралів.
3) Застосуємо властивість (3.1.3) 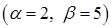 до табличного інтеграла 3):
до табличного інтеграла 3): 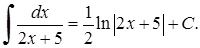
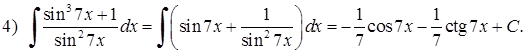 Почленним діленням інтеграл звівся до табличних 6) і 9) з урахуванням властивості (3.1.3)
Почленним діленням інтеграл звівся до табличних 6) і 9) з урахуванням властивості (3.1.3) 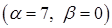 .
.
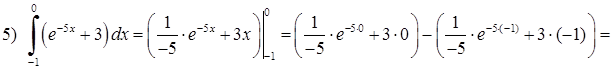
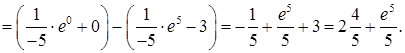 Тут застосовано властивість (3.1.3)
Тут застосовано властивість (3.1.3) 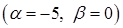 до табличнго інтеграла 4), а також табличний інтеграл 1) та формулу Ньютона-Лейбніца (3.1.8).
до табличнго інтеграла 4), а також табличний інтеграл 1) та формулу Ньютона-Лейбніца (3.1.8).
Приклад 3.1.2. Знайти методом заміни змінної (підстановки) невизначені та визначені інтеграли: 1) 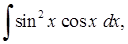
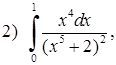 3)
3) 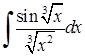 , 4)
, 4) 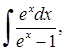 5)
5) 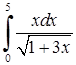 .
.
Розв’язання. 1) Нехай 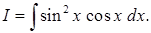 В підінтегральному виразі маємо функцію
В підінтегральному виразі маємо функцію 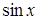 і її диференціал
і її диференціал 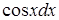 (нагадаємо, що
(нагадаємо, що 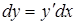 ). Роблячи заміну
). Роблячи заміну 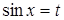 , знаходимо
, знаходимо 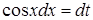 . Будемо мати
. Будемо мати 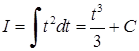 . Повертаючись до попередньої змінної, остаточно знайдемо
. Повертаючись до попередньої змінної, остаточно знайдемо 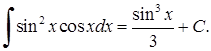
|
|
|
Розв’язок можна оформити таким чином:
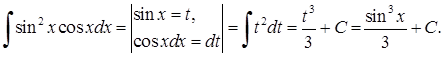
Можна також використовувати і такий запис:
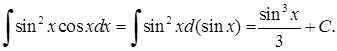
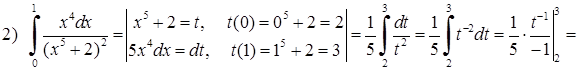
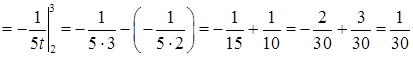 . Тут заміняючи змінну у визначеному інтегралі, знайшли нові межі інтегрування:
. Тут заміняючи змінну у визначеному інтегралі, знайшли нові межі інтегрування: 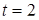 та
та 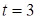 . Для цього обчислили значення нової змінної
. Для цього обчислили значення нової змінної  при
при 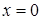 та
та 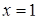 (це попередні межі інтегрування). Можна також використовувати і такий запис:
(це попередні межі інтегрування). Можна також використовувати і такий запис:
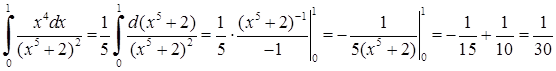 .
.
3) 
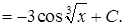
4) 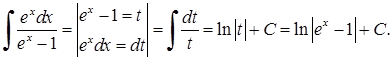
5) 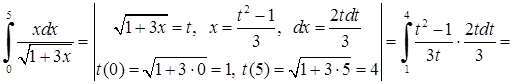
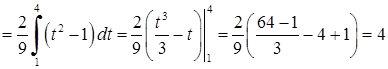 .
.
Приклад 3.1.3. Знайти інтегруванням частинами невизначені та визначені інтеграли: 1) 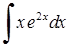 , 2)
, 2) 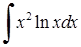 , 3)
, 3) 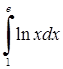 , 4)
, 4) 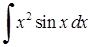 , 5)
, 5) 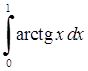 .
.
Розв’язання. 1)
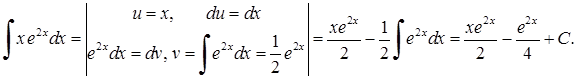
В цьому випадку в якості 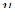 беремо
беремо 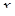 , бо маємо добуток виду
, бо маємо добуток виду  . Щоб інтеграл прийняв вид
. Щоб інтеграл прийняв вид 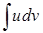 , позначимо
, позначимо 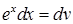 . Щоб скористатися формулою інтегрування частинами (3.1.11) треба знайти
. Щоб скористатися формулою інтегрування частинами (3.1.11) треба знайти 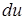 і
і 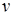 , тому рівняння
, тому рівняння 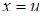 продиференцюємо, а в рівнянні
продиференцюємо, а в рівнянні 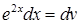 знайдемо первісну (скористаємось також властивістю (3.1.3) інтеграла).
знайдемо первісну (скористаємось також властивістю (3.1.3) інтеграла).
2) 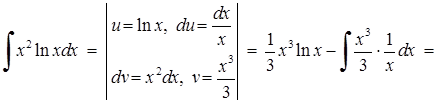
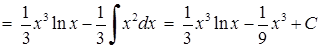 . В даному випадку підінтегральна функція має вид
. В даному випадку підінтегральна функція має вид 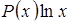 , а тому в якості
, а тому в якості 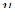 слід обрати
слід обрати 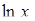 .
.
3) 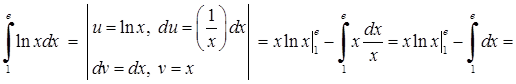
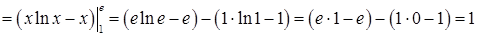 . Тут застосовано формулу інтегрування частинами (3.1.11) для визначеного інтеграла.
. Тут застосовано формулу інтегрування частинами (3.1.11) для визначеного інтеграла.
4) 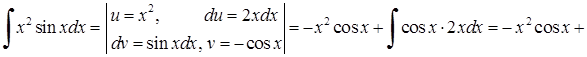
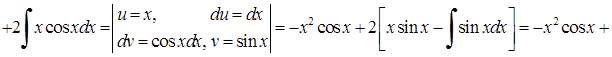
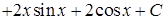 . Формулу (3.1.11) тут довелося використати двічі.
. Формулу (3.1.11) тут довелося використати двічі.
5) 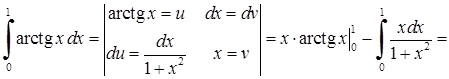
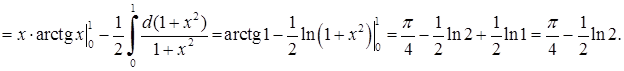
Приклад 3.1.4. Знайти інтеграли від раціональної або ірраціональної функції шляхом виділення повного квадрату у знаменнику: 1) 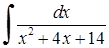 , 2)
, 2)  , 3)
, 3) 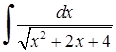 , 4)
, 4) 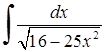
|
|
|
Розв’язання. 1)
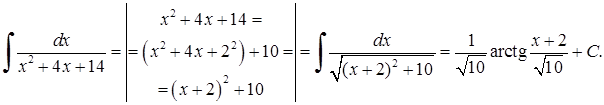 Тут застосовано властивість (3.1.3)
Тут застосовано властивість (3.1.3)  до табличного інтеграла 12)
до табличного інтеграла 12)  .
.
2) 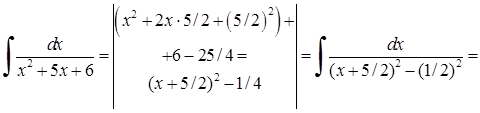
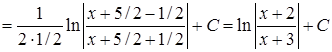 . Тут застосовано формулу (3.1.3)
. Тут застосовано формулу (3.1.3) 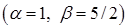 до табличного інтеграла 13)
до табличного інтеграла 13) 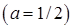 .
.
3) 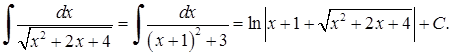 Тут застосовано властивість (3.1.3)
Тут застосовано властивість (3.1.3) 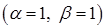 до табличного інтеграла 15)
до табличного інтеграла 15) 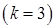 .
.
4) 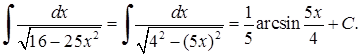 Тут застосовано формулу (3.1.3)
Тут застосовано формулу (3.1.3) 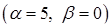 до табличного інтеграла 14)
до табличного інтеграла 14)  .
.
Приклад 3.1.5. Знайти способом перетворення добутків тригонометричних функцій у суми інтеграли: 1) 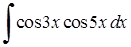 , 2)
, 2) 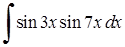 .
.
Розв’язання. За допомогою тригонометричних формул маємо:
1) 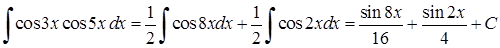 .
.
2) 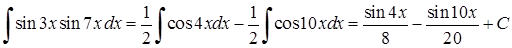 .
.
Зауважимо, що приклади 3.1.1 – 3.1.5 відповідають завданню 3.1 контрольної роботи.
Література: [1, с. 211 ‑ 252], [2, с. 308 ‑ 338], [3, с. 444 – 479, 509 ‑ 513], [11].
Невласні інтеграли
Інтеграли з нескінченними межами інтегрування й інтеграли від розривних функцій називаються невласними. Невласний інтеграл з нескінченною верхньою межею функції (неперервної при 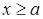 ):
):
. (3.2.1)
Якщо ця границя існує і є скінченною, то невласний інтеграл називається збіжним, у протилежному випадку - розбіжним. Аналогічно визначається невласний інтеграл із нескінченною нижньою межею,
, (3.2.2)
а також із двома нескінченними межами:
. (3.2.3)
Якщо неперервна при 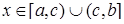 і
і 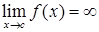 , то
, то
. (3.2.4)
Приклад 3.2.1. Дослідити на збіжність невласні інтеграли: 1) 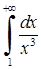 , 2)
, 2) 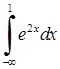 , 3)
, 3) 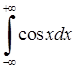 , 4)
, 4) 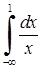 .
.
Розв’язання. 1) 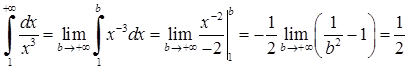 .
.
Границя існує і скінченна, тому невласний інтеграл збігається.
2)  . Границя існує і скінченна, тому невласний інтеграл збігається.
. Границя існує і скінченна, тому невласний інтеграл збігається.
3) 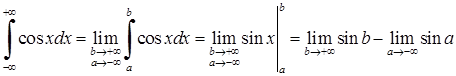 . Границі не існують, тому невласний інтеграл розбігається.
. Границі не існують, тому невласний інтеграл розбігається.
4) 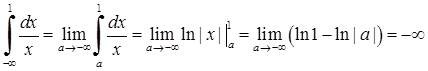 . Границя існує, але нескінченна, тому невласний інтеграл розбігається.
. Границя існує, але нескінченна, тому невласний інтеграл розбігається.
Зауважимо, що приклад 3.2.1 відповідає завданню 3.2 контрольної роботи.
Література: [1, с. 253 ‑ 255], [2, с. 375 ‑ 382], [3, с. 559 – 565], [11].
Дата добавления: 2018-09-22; просмотров: 887; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!