Системи рівнянь, вектори та аналітична геометрія

Стр 1 из 15Следующая ⇒

Міністерство освіти і науки України

Донецький Національний університет

економіки і торгівлі

Імені Михайла Туган-Барановського

Кафедра вищої і прикладної математики

В.Є. Силенко

ВИЩА МАТЕМАТИКА

МЕТОДИЧНІ РЕКОМЕНДАЦІЇ

для самостійної роботи студентів заочної форми навчання

напряму підготовки «Машинобудування»

(у рамках ECTS)

Затверджено

На засіданні кафедри

Вищої і прикладної математики

Протокол № 33 від 21.06.2010 р.

Схвалено навчально-методичною

Радою університету

Протокол № від

Донецьк 2010

ББК 22.1я73

С 36

УДК 51(076.5)

Рецензенти:

канд. фіз.-мат. наук, доцент Латинін С.М.,

Саркіс’янц О.В.

Силенко, В.Є.

Вища математика [Текст]: метод. рек. для самост. роботи студ. заоч. форми навч. напряму підготовки “Машинобудування” (у рамках ECTS) / М-во освіти і науки України, Донец. нац. ун-т економіки і торгівлі ім. М. Туган-барановського, Каф. вищ. і приклад. математики; В.Є. Силенко. – Донецьк: [ДонНУЕТ], 2010. – 147 с.

Методичні рекомендації призначені для організації самостійної роботи студентів заочної форми навчання (напряму підготовки “Машинобудування” інституту харчових виробництв) за курсом “Вища математика” у відповідності з новими стандартами підготовки фахівців інженерного профілю в рамках ECTS. Вона може бути використана також студентами інших спеціальностей і форм навчання.

Розробка містить деякі теоретичні питання, конкретні рекомендації і докладні коментарі прикладів розв’язування завдань основних типів відповідного змісту, а також індивідуальні завдання для самостійної роботи студентів.

ББК 22.1я73

Ó В.Є. Силенко Ó Донецький національний університет економіки і торгівлі імені Михайла Туган-Барановського, 2010

Зміст


Вступ…………………………………………………………………………..			5
Основні питання програми.……………………………………………….			6
МОДУЛЬ 1. Системи рівнянь, вектори та аналітична геометрія….…			9
	1.1.	Визначники, матриці, розв’язання систем лінійних рівнянь методами оберненої матриці, Крамера, Гаусса..….………….	9
	1.2.	Елементи векторної алгебри……………………………………	14
	1.3.	Пряма на площині...……………………….……………………..	17
	1.4.	Криві другого порядку………………………….…...……….….	18
	1.5.	Площина та пряма в просторі…………………………………..	19
МОДУЛЬ 2. Вступ в математичний аналіз………………………………			22
	2.1.	Розкриття невизначеностей, І і ІІ визначні границі...…...…..	22
	2.2.	Диференціальне числення функцій однієї змінної.…...……	26
	2.3.	Застосування похідних для дослідження функцій.…...……..	29
	2.4.	Похідні в механіці.…...…….…...…….…...…….…......…...…….	33
	2.5.	Диференціальне числення функцій декількох змінних……	33
МОДУЛЬ 3. Невизначений і визначений інтеграли…………………...			37
	3.1.	Основні методи інтегрування………………………..………...	37
	3.2.	Невласні інтеграли……………………………….….…...……....	44
	3.3.	Застосування визначених інтегралів……….…...……………..	46
МОДУЛЬ 4. Диференціальні рівняння……………………………..…...			48
	4.1.	Розв’язання диференціальних рівнянь деяких типів………..	48
МОДУЛЬ 5. Кратні, криволінійні та поверхневі інтеграли...…………			54
	1.1.	Подвійні, потрійні інтеграли та їх застосування…………….	54
	1.2.	Криволінійні інтеграли….…….……………………..………….	58
МОДУЛЬ 6. Числові і степеневі ряди..…………….…………………….			61
	6.1.	Числові ряди………………………………………..……………..	61
	6.2.	Степеневі ряди.………………..……………………..…………...	65
МОДУЛЬ 7. Комплексні числа. Елементи теорії функцій комплексної змінної……………….……………………….			68
	7.1.	Комплексні числа………………….……………………..……….	68
	7.2.	Обчислення значень елементарних функцій комплексної змінної...………………………………..…..……………………....	73
МОДУЛЬ 8. Теорія ймовірностей і елементи математичної статистики…………….…………………….…………….….			76
	8.1.	Основні поняття і теореми теорії ймовірностей……………..	76
	8.2.	Дискретні випадкові величини..………………….…………….	86
	8.3.	Неперервні випадкові величини.…………………….………...	91
	8.4.	Біноміальний та пуассонів закони розподілу..…….…………	94
	8.5.	Нормальний, рівномірний та показниковий закони розподілу ймовірностей.………........................……………..…	95
	8.6.	Елементи математичної статистики.…………………………..	99
Контрольна робота № 1……………………………………………………			103
Контрольна робота № 2……………………………………………………			125
Література……………………………………………………………………			156
Додаток А. Таблиця значень функції Гаусса …………………...			158
Додаток Б. Таблиця значень функції Лапласа ………………...			160
Додаток В. Розподіл Пуассона……………………………………..….....			161

ВСТУП

Математична підготовка у ВНЗ ‑ важлива складова професійної компетентності майбутнього фахівця інженерного профілю. Математика як мова наукових досліджень сприяє формуванню наукового світогляду, інтелектуальному розвитку творчого потенціалу студентів, у тому числі логічного й абстрактного мислення. Широке застосування математичних методів ‑ характерна риса сучасної науки. Вивчення курсу вищої математики є передумовою оволодіння студентами основними методами аналізу і моделювання дійсності та розв'язання за їх допомогою практичних професійних задач.

Основною для студента заочної форми навчання є самостійна робота, що складається з вивчення теоретичного матеріалу за підручником, розв’язання задач і виконання контрольної роботи.

Методичні рекомендації внаслідок їх компактності висвітлюють лише ключові моменти курсу вищої математики та містять розв'язання найтиповіших задач. Наведені в розробці основні питання програми та посилання на відповідні посібники повинні допомогти студентові засвоїти курс у цілому. Розробка містить дві контрольні роботи для виконання в першому та другому семестрах відповідно. Номер кожної задачі контрольної роботи має вигляд z.y.x, де z та y – порядкові номери змістового модуля та задачі у цьому модулі відповідно, x – номер варіанта. Для виконання слід обрати всі задачі свого варіанта.

Вибір варіанта здійснюється таким чином. Якщо дві останні цифри номера залікової книжки утворюють число, що є не більшим 30, то це число і є номером варіанта. Якщо ж це число більше 30, то треба відняти від нього кратне 30, щоб отримати номер варіанта. Наприклад, дві останні цифри номера залікової книжки 78, тоді , тобто отримали варіант № 18. Останні цифри 00 ‑ беремо варіант № 30.

Робота, що виконана не за своїм варіантом, не зараховується.

Правила оформлення контрольної роботи:

· контрольну роботу слід виконувати в окремому зошиті, залишаючи поля для зауважень викладача,

· у заголовку роботи (на обкладинці зошита) треба вказати прізвище та ініціали, факультет, курс, групу, номер залікової книжки,

· розв'язання слід виконувати послідовно для кожного модуля в порядку зростання номерів задач,

· перед розв'язанням кожної задачі потрібно записати її умову,

· розв'язок задач треба викладати докладно, пояснюючи дії,

· наприкінці контрольної роботи необхідно перелічити використану для виконання літературу.

Захист контрольної роботи проводиться у формі співбесіди.

Методична розробка присвячується світлій пам'яті Сільченка Василя Опанасовича, який багато років плідно викладав курс вищої математики студентам спеціальності “Обладнання переробних і харчових виробництв”.

ОСНОВНІ ПИТАННЯ ПРОГРАМИ

I семестр
Змістовий модуль І. Системи рівнянь, вектори та аналітична геометрія.
Тема 1.	Визначники ІІ-го, ІІІ-го порядків, їх властивості, розв’язання систем методами Гаусса і Крамера.
Тема 2.	Матриці, властивості та дії над ними, застосування до розв’язання систем лінійних рівнянь.
Тема 3.	Елементи векторної алгебри (скалярний, векторний та мішаний добутки).
Тема 4.	Прямі лінії на площині. Канонічні рівняння кола, еліпса, гіперболи, параболи.
Тема 5.	Площина, різні види її рівнянь, пряма в просторі, різні види її рівнянь, сумісний розгляд прямої та площини.
Змістовий модуль ІI. Вступ в математичний аналіз.
Тема 6.	Функції та послідовності і їх границі. Умови існування границі, І і ІІ визначні границі.
Тема 7.	Диференціальне числення функцій однієї змінної.
Тема 8.	Диференціальне числення функцій декількох змінних.
Тема 9.	Застосування похідних в геометрії і механіці.
Змістовий модуль ІII. Невизначений і визначений інтеграли.
Тема 10.	Невизначений інтеграл, означення, способи обчислення, обчислення інтегралів різних типів функцій.
Тема 11.	Визначений інтеграл, означення, інтегрування за частинами та заміна змінних у визначеному інтегралі. Невласні інтеграли.
Тема 12.	Застосування визначених інтегралів при обчисленні геометричних, механічних та фізичних величин.

Змістовий модуль ІV. Диференціальні рівняння.
Тема 13.	Диференціальні рівняння 1-ого порядку з відокремлюваними змінними.
Тема 14.	Лінійні рівняння 1-ого порядку.
Тема 15.	Однорідні диференціальні рівняння 1-ого порядку.
Тема 16.	Однорідні і неоднорідні диференціальні рівняння 2-го порядку зі сталими коефіцієнтами. Методи характеристичного рівняння та невизначених коефіцієнтів.

II семестр
Змістовий модуль V. Кратні, криволінійні та поверхневі інтеграли.
Тема 17.	Подвійні інтеграли, означення, обчислення в декартових і полярних координатах. Застосування в геометрії і механіці.
Тема 18.	Потрійні інтеграли, означення, обчислення в декартових, циліндричних і сферичних координатах. Застосування в геометрії і механіці.
Тема 19.	Криволінійні інтеграли І і ІІ родів, означення, обчислення та застосування.
Тема 20.	Поверхневі інтеграли І і ІІ роду, означення, обчислення та застосування.
Змістовий модуль VI. Числові і степеневі ряди.
Тема 21.	Числові знакододатні ряди. Збіжність ряду та його сума. Необхідна ознака збіжності. Достатні ознаки збіжності знакододатних рядів. Проста та гранична ознаки порівняння. Ознаки Даламбера та Коші.
Тема 22.	Інтегральна ознака Коші. Знакочергувальний ряд Лейбніца. Ряди з довільними за знаком членами. Абсолютна і умовна збіжності.
Тема 23.	Функціональний ряд. Мажорованість ряду. Степеневі ряди. Теорема Абеля. Знаходження інтервалу збіжності.
Тема 24.	Розвинення функцій 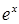, , 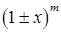, 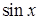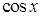в степеневі ряди Маклорена. Застосування рядів.
Змістовий модуль VII. Комплексні числа. Елементи теорії функцій комплексного змінного .
Тема 25.	Комплексні числа та дії над ними. Алгебраїчна, тригонометрична та показникова форми комплексного числа. Піднесення до степеня та добування кореня із комплексного числа.
Тема 26.	Основні елементарні функції комплексного змінного.
Тема 27.	Аналітичність функції комплексного змінного. Умови аналітичності Коші-Рімана.
Тема 28.	Обчислення частинних значень елементарних функцій комплексного змінного. Конформність відображень за допомогою функцій комплексного змінного.
Змістовий модуль VІІІ. Теорія ймовірностей і елементи математичної статистики .
Тема 29.	Предмет і основні поняття теорії ймовірностей. Класична ймовірність. Основні теореми теорії ймовірностей.
Тема 30.	Схема незалежних повторних випробувань, формула Бернуллі, локальна і інтегральна теорема Лапласа, формула Пуассона.
Тема 31.	Закони розподілу ймовірностей. Інтегральна та диференціальна функції розподілу. Числові характеристики дискретних і неперервних випадкових величин. Рівномірний, показниковий та нормальний розподіли.
Тема 32.	Елементи математичної статистики. Вибірковий метод. Точкові і інтервальні оцінки параметрів розподілу. Кореляційна залежність.

МОДУЛЬ 1

Системи рівнянь, вектори та аналітична геометрія

Дата добавления: 2018-09-22; просмотров: 242; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!
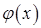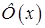