Застосування визначених інтегралів
Інтеграли 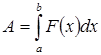 (робота змінної сили
(робота змінної сили 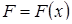 на відрізку
на відрізку 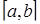 ),
), 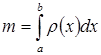 (маса лінійного стержня з неоднорідною густиною
(маса лінійного стержня з неоднорідною густиною 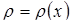 на відрізку
на відрізку 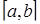 ) і
) і 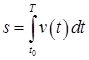 (довжина шляху, який пройшла матеріальна точка, що рухалась прямолінійно із змінною швидкістю
(довжина шляху, який пройшла матеріальна точка, що рухалась прямолінійно із змінною швидкістю 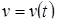 впродовж часу
впродовж часу  ) виражають різні аспекти фізичного змісту визначеного інтеграла.
) виражають різні аспекти фізичного змісту визначеного інтеграла.
Площа фігури, обмеженої знизу і зверху двома неперервними кривими  і
і 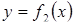 (
( 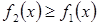 ), а зліва і справа – відповідно прямими
), а зліва і справа – відповідно прямими 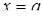 ,
, 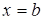 , обчислюється за формулою:
, обчислюється за формулою:
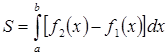 . (3.3.1)
. (3.3.1)
Для однорідної (з постійною густиною маси) криволінійної трапеції ‑ фігури, обмеженої неперервною кривою 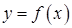 , віссю
, віссю 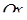
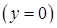 та двома прямими
та двома прямими 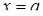 і
і 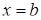
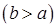 , координати центра маси:
, координати центра маси:
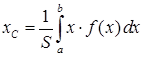 ,
, 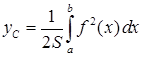 , (3.3.2)
, (3.3.2)
де 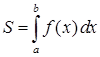 – площа криволінійної трапеції.
– площа криволінійної трапеції.
При обертанні цієї криволінійної трапеції навколо вісі 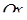 отримаємо тіло, об'єм якого
отримаємо тіло, об'єм якого
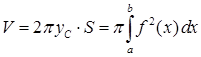 . (3.3.3)
. (3.3.3)
Приклад 3.3.1. За допомогою інтегрального числення для обмеженої лініями 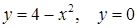 плоскої фігури
плоскої фігури 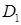 : а) обчислити площу, б) знайти координати центра ваги, якщо густина маси
: а) обчислити площу, б) знайти координати центра ваги, якщо густина маси 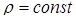 , в) обчислити об’єм тіла, що утворюється при обертанні фігури
, в) обчислити об’єм тіла, що утворюється при обертанні фігури 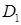 навколо вісі
навколо вісі 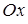 .
.
Розв’язання.
 |
Криволінійна трапеція
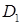 обмежена зверху – параболою
обмежена зверху – параболою 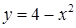 , знизу ‑ віссю
, знизу ‑ віссю 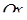
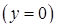 та проектується на відрізок
та проектується на відрізок 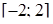 осі
осі 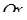 .
.
Рис. 3.3.1 ‑ Криволінійна трапеція 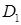
а) Площа згідно (3.3.1): 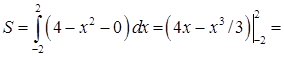
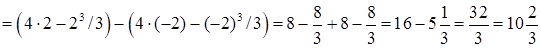 (кв. од.),
(кв. од.),
б) Координати центра мас за формулами (3.3.2): 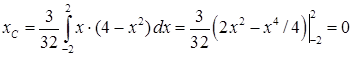 ,
, 
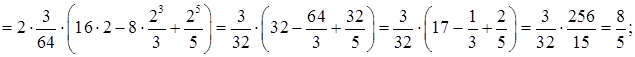
в) Об’єм тіла обертання згідно (3.3.3): 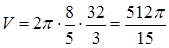 (куб. од.)
(куб. од.)
|
|
|
Зауважимо, що приклад 3.3.1 відповідає завданню 3.3 контрольної роботи.
Література: [1, с. 256 ‑ 272], [2, с. 339 ‑ 365], [3, с. 577 – 581], [11].
МОДУЛЬ 4
ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ
Розв’язання диференціальних рівнянь деяких типів
Рівняння, в яких є незалежні змінні, невідома функція однієї змінної і її похідні (або диференціали), називається звичайним диференціальним. Порядок диференціального рівняння – це порядок найвищої похідної. Диференціальне рівняння першого порядку має вигляд: 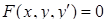 , або
, або 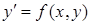 , другого порядку:
, другого порядку: 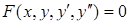 , або
, або  . Розв’язком диференціального рівняння на інтервалі
. Розв’язком диференціального рівняння на інтервалі 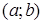 називається диференційовна на цьому інтервалі функція
називається диференційовна на цьому інтервалі функція 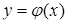 , яка перетворює це рівняння на тотожність при всіх
, яка перетворює це рівняння на тотожність при всіх 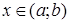 . Відповідно інтеграл – це розв’язок у неявному вигляді. Загальний розв’язок рівняння n-го порядку містить п довільних незалежних постійних.
. Відповідно інтеграл – це розв’язок у неявному вигляді. Загальний розв’язок рівняння n-го порядку містить п довільних незалежних постійних.
Диференціальне рівняння
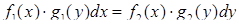 , (4.1.1)
, (4.1.1)
або
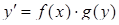 (4.1.2)
(4.1.2)
називається рівнянням з відокремлюваними змінними. Після відокремлення змінних (ураховуючи, що 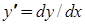 ), тобто отримання рівняння
), тобто отримання рівняння 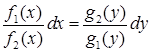 (або
(або 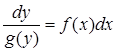 ) залишається здійснити інтегрування кожної частини за відповідною змінною. Одержимо загальний інтеграл
) залишається здійснити інтегрування кожної частини за відповідною змінною. Одержимо загальний інтеграл 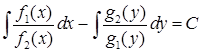 , (або
, (або 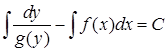 ).
).
|
|
|
Однорідне диференціальне рівняння першого порядку
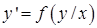 (4.1.3)
(4.1.3)
можна привести до рівняння з відокремлюваними змінними за допомогою підстановки
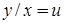 , або
, або 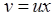 ,
, 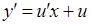 . (4.1.4)
. (4.1.4)
Лінійне рівняння має вигляд
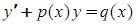 , (4.1.5)
, (4.1.5)
причому якщо 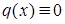 , то лінійне рівняння є однорідним, у протилежному випадку – неоднорідним. Розв’язання лінійного неоднорідного рівняння зводиться до розв’язання двох рівнянь з відокремлюваними змінними за допомогою заміни:
, то лінійне рівняння є однорідним, у протилежному випадку – неоднорідним. Розв’язання лінійного неоднорідного рівняння зводиться до розв’язання двох рівнянь з відокремлюваними змінними за допомогою заміни:
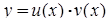 , (4.1.6)
, (4.1.6)
де  – допоміжні функції. Тоді
– допоміжні функції. Тоді  , і вихідне рівняння набуває виду:
, і вихідне рівняння набуває виду: 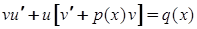 . Одну із допоміжних функцій, наприклад
. Одну із допоміжних функцій, наприклад 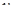 , можна обрати довільно, припустимо такою, щоб вираз в квадратних дужках дорівнював нулеві. Тоді матимемо два рівняння:
, можна обрати довільно, припустимо такою, щоб вираз в квадратних дужках дорівнював нулеві. Тоді матимемо два рівняння: 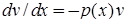 і
і 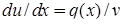 . Підстановка частинного розв’язку першого рівняння
. Підстановка частинного розв’язку першого рівняння 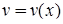 дозволяє знайти загального розв’язок
дозволяє знайти загального розв’язок 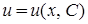 другого рівняння з відокремлюваними змінними. Після чого можна записати загальний розв’язок вихідного рівняння:
другого рівняння з відокремлюваними змінними. Після чого можна записати загальний розв’язок вихідного рівняння: 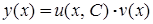 .
.
Лінійне однорідне диференціальне рівняння другого порядку зі сталими коефіцієнтами має вид:
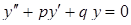 , (4.1.7)
, (4.1.7)
|
|
|
де 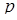 і
і 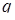 – числа,
– числа,  ‑ функція. Структура загального розв’язку цього рівняння залежить від характеру коренів
‑ функція. Структура загального розв’язку цього рівняння залежить від характеру коренів 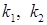 характеристичного рівняння
характеристичного рівняння 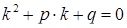 .
.
v Якщо корені різні 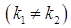 і дійсні (характеристичне рівняння має дискримінант
і дійсні (характеристичне рівняння має дискримінант 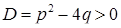 ), то
), то
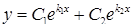 , (4.1.8)
, (4.1.8)
де 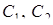 – довільні сталі.
– довільні сталі.
v Якщо корені характеристичного рівняння рівні 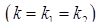 і дійсні (
і дійсні ( 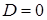 ), то
), то
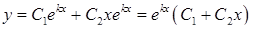 . (4.1.9)
. (4.1.9)
v Якщо  , то корені
, то корені 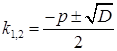 характеристичного рівняння є комплексно-спряженими (дивись розділ 7 та приклад 7.1.7) числами
характеристичного рівняння є комплексно-спряженими (дивись розділ 7 та приклад 7.1.7) числами 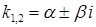 , і тоді
, і тоді
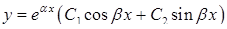 . (4.1.10)
. (4.1.10)
Приклад 4.1.1. Знайти загальний розв’язок (або загальний інтеграл) диференціальних рівнянь першого порядку: 1) 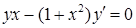 , 2)
, 2) 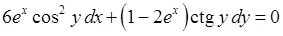 .
.
Розв’язання. 1) З рівняння 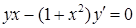 виразимо похідну:
виразимо похідну: 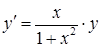 . Таким чином, це диференціальне рівняння є рівнянням з відокремлюваними змінними (4.1.2) (у даному випадку
. Таким чином, це диференціальне рівняння є рівнянням з відокремлюваними змінними (4.1.2) (у даному випадку 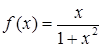 ,
, 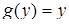 ). Враховуючи, що
). Враховуючи, що 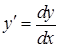 , відокремимо змінні:
, відокремимо змінні: 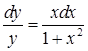 . Тепер можна інтегрувати:
. Тепер можна інтегрувати: 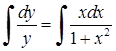 ,
, 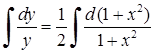 (бо
(бо 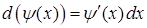 ). Отримаємо:
). Отримаємо: 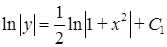 ‑ загальний інтеграл диференціального рівняння. Записуючи довільну постійну у вигляді
‑ загальний інтеграл диференціального рівняння. Записуючи довільну постійну у вигляді  , маємо:
, маємо: 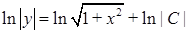 ,
, 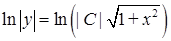 , тобто
, тобто 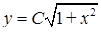 ‑ загальний розв'язок.
‑ загальний розв'язок.
2) Рівняння 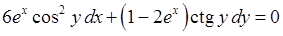 є рівнянням з відокремлюваними змінними (4.1.1) (у даному випадку
є рівнянням з відокремлюваними змінними (4.1.1) (у даному випадку 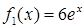 ,
, 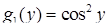 ,
, 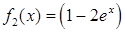 ,
, 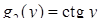 ). Відокремимо змінні:
). Відокремимо змінні: 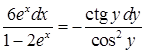 . Тепер можна інтегрувати:
. Тепер можна інтегрувати: 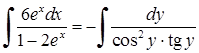 ,
, 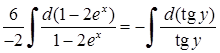 ,
, 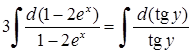 (бо
(бо 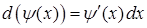 ,
,  ). Отримаємо:
). Отримаємо: 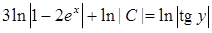 ,
, 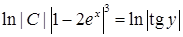 , отже
, отже 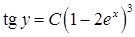 ‑ загальний інтеграл.
‑ загальний інтеграл.
|
|
|
Приклад 4.1.2. Знайти загальний розв’язок (або загальний інтеграл) диференціальних рівнянь першого порядку: 1) 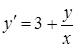 , 2)
, 2) 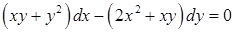 .
.
Розв’язання. 1) Бачимо, що 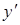 є функцією відношення
є функцією відношення 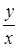 , тобто рівняння
, тобто рівняння 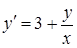 є однорідним (має вид (4.1.3)). Вводимо нову функцію
є однорідним (має вид (4.1.3)). Вводимо нову функцію 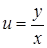 , тоді
, тоді 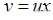 і
і 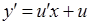 . Вихідне рівняння перетворюється в рівняння з відокремлюваними змінними:
. Вихідне рівняння перетворюється в рівняння з відокремлюваними змінними: 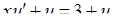 , або
, або 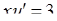 ,
, 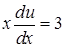 , звідки
, звідки 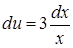 . Змінні відокремлено, отже можна інтегрувати:
. Змінні відокремлено, отже можна інтегрувати: 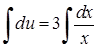 ,
, 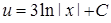 . Значить,
. Значить, 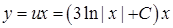 . Отже,
. Отже, 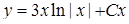 ‑ загальний розв'язок.
‑ загальний розв'язок.
2) Виразимо похідну 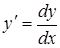 , тоді рівняння
, тоді рівняння 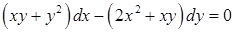 матиме вигляд:
матиме вигляд:  , а після ділення чисельника і знаменника правої частини на
, а після ділення чисельника і знаменника правої частини на 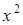 матимемо:
матимемо:
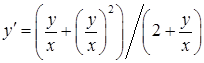 . (4.1.11)
. (4.1.11)
Бачимо, що 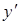 є функцією відношення
є функцією відношення 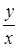 , тобто дане рівняння – однорідне. Вводимо нову функцію
, тобто дане рівняння – однорідне. Вводимо нову функцію 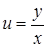 , тоді
, тоді 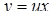 і
і 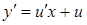 . Рівняння (4.1.11) перетворюється на рівняння з відокремлюваними змінними:
. Рівняння (4.1.11) перетворюється на рівняння з відокремлюваними змінними: 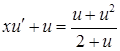 , або
, або 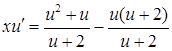 ,
, 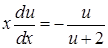 , звідки
, звідки 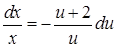 ,
, 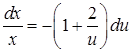 . Після інтегрування кожної частини за своєю змінною одержимо:
. Після інтегрування кожної частини за своєю змінною одержимо: 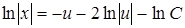 , або
, або 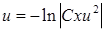 , звідки
, звідки  . Якщо замінити в останній рівності
. Якщо замінити в останній рівності 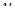 відношенням
відношенням 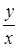 , то остаточно знаходимо загальний інтеграл вихідного рівняння:
, то остаточно знаходимо загальний інтеграл вихідного рівняння: 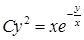 .
.
Приклад 4.1.3. Знайти загальний розв’язок (або загальний інтеграл) диференціальних рівнянь першого порядку: 1) 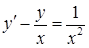 , 2)
, 2) 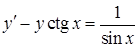 .
.
Розв’язання. 1) Диференціальне рівняння 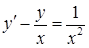 є лінійним неоднорідним рівнянням (4.1.5) (у даному випадку
є лінійним неоднорідним рівнянням (4.1.5) (у даному випадку 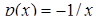 ,
, 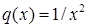 ). Покладаємо
). Покладаємо 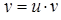 , тоді
, тоді 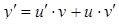 . Підставляємо
. Підставляємо 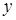 та
та 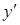 у вихідне рівняння:
у вихідне рівняння: 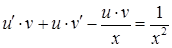 . Після групування маємо:
. Після групування маємо: 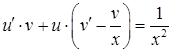 . Обираємо функцію
. Обираємо функцію 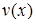 так, щоб вираз у дужках дорівнював нулеві. Дістанемо два рівняння з відокремлюваними змінними:
так, щоб вираз у дужках дорівнював нулеві. Дістанемо два рівняння з відокремлюваними змінними: 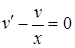 і
і 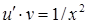 , або
, або 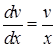 і
і 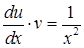 . Проінтегруємо:
. Проінтегруємо: 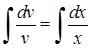 ,
, 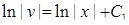 . Значить,
. Значить, 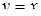 ‑ частинний розв’язок (при
‑ частинний розв’язок (при 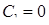 ) першого рівняння. Підставляємо знайдену функцію
) першого рівняння. Підставляємо знайдену функцію 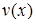 у друге рівняння:
у друге рівняння: 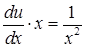 , звідки
, звідки 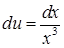 . Інтегруючи, знайдемо функцію
. Інтегруючи, знайдемо функцію 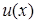 :
: 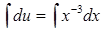 ,
, 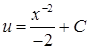 ,
, 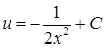 ‑ загальний розв’язок другого рівняння. Отже,
‑ загальний розв’язок другого рівняння. Отже, 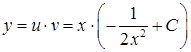 , і
, і  ‑ загальний розв’язок лінійного рівняння.
‑ загальний розв’язок лінійного рівняння.
2) Диференціальне рівняння 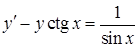 є лінійним неоднорідним рівнянням (4.1.5) (у даному випадку
є лінійним неоднорідним рівнянням (4.1.5) (у даному випадку 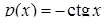 ,
, 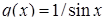 ). Покладаємо
). Покладаємо 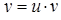 , тоді
, тоді 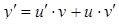 і дане рівняння набуває виду:
і дане рівняння набуває виду: 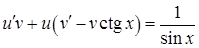 . Обираємо функцію
. Обираємо функцію 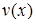 так, щоб вираз у дужках дорівнював нулеві. Дістанемо два рівняння з відокремлюваними змінними:
так, щоб вираз у дужках дорівнював нулеві. Дістанемо два рівняння з відокремлюваними змінними: 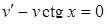 і
і 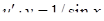 . Знаходимо частинний розв’язок першого рівняння:
. Знаходимо частинний розв’язок першого рівняння: 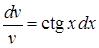 ,
,  ,
, 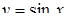 . Підстановка знайденої функції
. Підстановка знайденої функції 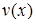 у друге рівняння приводить до рівняння:
у друге рівняння приводить до рівняння: 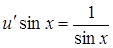 , звідки
, звідки 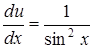 , або
, або 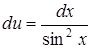 . Інтегрування останнього дає
. Інтегрування останнього дає 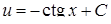 . Тоді шуканий загальний розв’язок вихідного рівняння:
. Тоді шуканий загальний розв’язок вихідного рівняння: 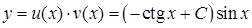 , тобто
, тобто 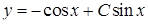 .
.
Приклад 4.1.4. Знайти загальний розв’язок лінійних однорідних диференціальних рівнянь другого порядку зі сталими коефіцієнтами: 1) 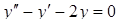 , 2)
, 2) 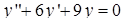 , 3)
, 3) 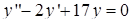 .
.
Розв’язання. 1) Запишемо характеристичне рівняння: 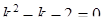 . Тоді
. Тоді 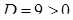 , і
, і 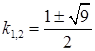 , отже
, отже 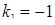 ,
, 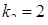 ‑ дійсні різні корені характеристичного рівняння. Значить, згідно (4.1.8)
‑ дійсні різні корені характеристичного рівняння. Значить, згідно (4.1.8) 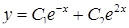 ‑ загальний розв’язок диференціального рівняння (
‑ загальний розв’язок диференціального рівняння ( 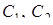 – довільні сталі).
– довільні сталі).
2) Запишемо характеристичне рівняння: 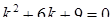 , або
, або 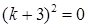 . Тоді
. Тоді 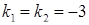 (
( 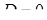 ), і таким чином за (4.1.9)
), і таким чином за (4.1.9) 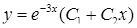 ‑ загальний розв’язок диференціального рівняння (
‑ загальний розв’язок диференціального рівняння ( 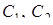 – довільні сталі).
– довільні сталі).
3) Характеристичне рівняння: 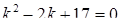 . Тоді
. Тоді 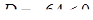 ,
, 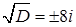 і
і 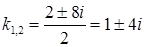 ‑ комплексно-спряжені корені характеристичного рівняння (
‑ комплексно-спряжені корені характеристичного рівняння ( 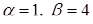 ). Значить, за (4.1.10)
). Значить, за (4.1.10) 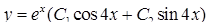 ‑ загальний розв’язок диференціального рівняння (
‑ загальний розв’язок диференціального рівняння ( 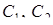 – довільні сталі).
– довільні сталі).
Зауважимо, що приклади 4.1.1 – 4.1.4 відповідають завданню 4.1 контрольної роботи.
Література: [1, с. 407 ‑ 457], [2, с. 501 ‑ 580], [4, с. 5 – 121], [12].
МОДУЛЬ 5
Дата добавления: 2018-09-22; просмотров: 297; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
