КРАТНІ, КРИВОЛІНІЙНІ ТА ПОВЕРХНЕВІ ІНТЕГРАЛИ
Подвійні, потрійні інтеграли та їх застосування
Основні види простих областей інтегрування на площині:
· Область інтегрування 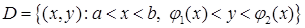 є стандартною відносно вісі
є стандартною відносно вісі 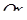 . Вона обмежена зліва і справа прямими
. Вона обмежена зліва і справа прямими 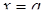 і
і 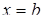
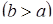 , а знизу і зверху – неперервними кривими
, а знизу і зверху – неперервними кривими 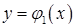 і
і 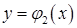
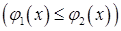 , кожна з яких перетинається вертикальною прямою
, кожна з яких перетинається вертикальною прямою 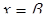 (для будь-якого
(для будь-якого 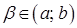 ), лише в одній точці.
), лише в одній точці.
Для такої області подвійний інтеграл обчислюється за формулою:
 , (5.1.1)
, (5.1.1)
причому спочатку обчислюється за змінною 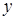 “внутрішній” інтеграл
“внутрішній” інтеграл 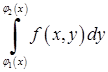 , в якому
, в якому 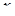 вважається сталим.
вважається сталим.
· Область інтегрування 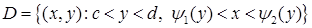 є стандартною відносно вісі
є стандартною відносно вісі  . Вона обмежена знизу і зверху прямими
. Вона обмежена знизу і зверху прямими 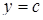 і
і 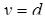
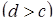 , а справа а зліва – відповідно неперервними кривими
, а справа а зліва – відповідно неперервними кривими 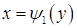 і
і 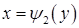
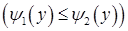 , кожна із яких перетинається довільною горизонтальною прямою
, кожна із яких перетинається довільною горизонтальною прямою 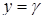 (для будь-якого
(для будь-якого 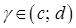 ) лише в одній точці.
) лише в одній точці.
Для такої області подвійний інтеграл обчислюється за формулою:
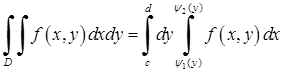 , (5.1.2)
, (5.1.2)
причому спочатку обчислюється за змінною  “внутрішній” інтеграл
“внутрішній” інтеграл 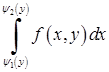 , в якому
, в якому 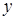 вважається сталим.
вважається сталим.
Праві частини формул (5.1.1), (5.1.2) називаються двократними, або повторними інтегралами. Таким чином, подвійний інтеграл обчислюється за допомогою зведення його до повторного інтеграла. Якщо область не є стандартною, то як часто трапляється, її можна представити у вигляді об’єднання стандартних множин.
Перетворення подвійного інтеграла в прямокутних декартових координатах 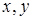 до інтеграла в полярних координатах
до інтеграла в полярних координатах 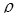 ,
, 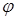 , які пов’язані з прямокутними координатами співвідношеннями
, які пов’язані з прямокутними координатами співвідношеннями
|
|
|
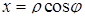 ,
, 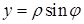 , (5.1.3)
, (5.1.3)
здійснюється за формулою:
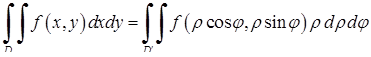 . (5.1.4)
. (5.1.4)
Якщо область 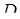 обмежена променями, які утворюють з полярною віссю кути
обмежена променями, які утворюють з полярною віссю кути 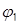 і
і 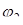
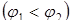 , і кривими
, і кривими 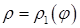 і
і 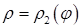
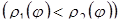 , то відповідні полярні координати змінюються в межах області
, то відповідні полярні координати змінюються в межах області 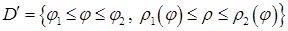 , і тоді
, і тоді
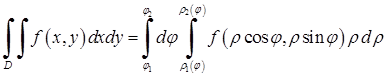 . (5.1.5)
. (5.1.5)
Приклад 5.1.1. Обчислити інтеграл 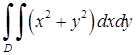 , де
, де 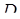 ‑ чверть круга
‑ чверть круга 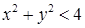 , що лежить в першій координатній чверті
, що лежить в першій координатній чверті 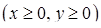 .
.
Розв’язання. У відповідності з формулами (5.1.4), (5.1.5):
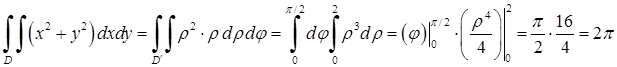 .
.
Площа плоскої фігури 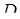 виражається формулою
виражається формулою
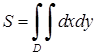 . (5.1.6)
. (5.1.6)
Об’єм циліндричного тіла (обмеженого зверху неперервною поверхнею 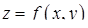 , знизу – площиною
, знизу – площиною 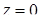 і з боків – циліндричною поверхнею з твірними, паралельними осі
і з боків – циліндричною поверхнею з твірними, паралельними осі 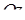 ), що вирізає на площині
), що вирізає на площині 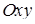 область
область 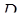 , обчислюється за формулою:
, обчислюється за формулою:
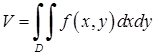 . (5.1.7)
. (5.1.7)
Якщо пластинка займає область 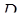 площини
площини 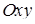 і має змінну поверхневу густину
і має змінну поверхневу густину 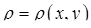 , то маса пластинки виражається подвійним інтегралом
, то маса пластинки виражається подвійним інтегралом
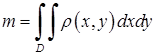 . (5.1.8)
. (5.1.8)
Координати центра мас обчислюються за формулами:
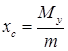 ,
, 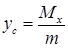 , (5.1.9)
, (5.1.9)
де 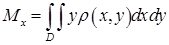 ,
, 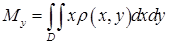 .
.
Якщо область інтегрування  визначається нерівностями
визначається нерівностями 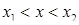 ,
, 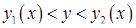 ,
, 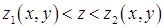 , де
, де  ,
, 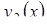 ,
, 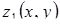 ,
, 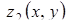 – неперервні функції, то потрійний інтеграл від функції
– неперервні функції, то потрійний інтеграл від функції 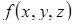 по області
по області  , обчислюється за формулою:
, обчислюється за формулою:
|
|
|
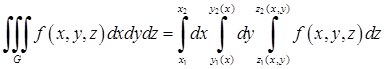 . (5.1.10)
. (5.1.10)
Об’єм просторового тіла, що займає область  , визначається за формулою:
, визначається за формулою:
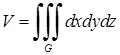 . (5.1.11)
. (5.1.11)
Якщо  – деяка область простору, яку займає матеріальне тіло з густиною
– деяка область простору, яку займає матеріальне тіло з густиною 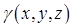 , то маса тіла
, то маса тіла  визначається формулою:
визначається формулою:
 . (5.1.12)
. (5.1.12)
Приклад 5.1.2. Для фігури 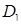 , що обмежена лініями, вказаними в прикладі 3.3.1: а) записати подвійний інтеграл
, що обмежена лініями, вказаними в прикладі 3.3.1: а) записати подвійний інтеграл 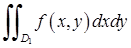 (
( 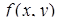 ‑ неперервна функція в
‑ неперервна функція в 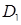 ) у вигляді повторного інтеграла та змінити порядок інтегрування; б) знайти масу пластини
) у вигляді повторного інтеграла та змінити порядок інтегрування; б) знайти масу пластини 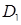 , якщо густина маси
, якщо густина маси 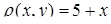 ; в) обчислити об’єм циліндричного тіла
; в) обчислити об’єм циліндричного тіла 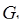 , обмеженого зверху площиною
, обмеженого зверху площиною 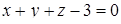 , знизу – площиною
, знизу – площиною 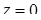 і з боків – прямою циліндричною поверхнею, що вирізає на площині
і з боків – прямою циліндричною поверхнею, що вирізає на площині 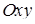 область
область  ; г) знайти масу циліндричного тіла
; г) знайти масу циліндричного тіла 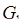 , якщо густина маси
, якщо густина маси 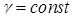 .
.
Розв’язання. а) Криволінійна трапеція 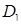 (див. рис. 3.3.1) обмежена зверху – параболою
(див. рис. 3.3.1) обмежена зверху – параболою 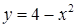 , знизу ‑ віссю
, знизу ‑ віссю 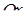
 та проектується на відрізок
та проектується на відрізок 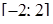 осі
осі 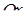 . Значить,
. Значить, 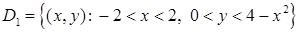 є стандартною відносно вісі
є стандартною відносно вісі  .
.
З іншого боку, 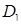 обмежена зліва – віткою параболи
обмежена зліва – віткою параболи  , справа – віткою параболи
, справа – віткою параболи 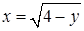 та проектується на відрізок
та проектується на відрізок 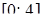 осі
осі 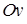 . Таким чином,
. Таким чином,  є стандартною відносно вісі
є стандартною відносно вісі 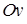 .
.
|
|
|
Отже, запишемо подвійний інтеграл у вигляді обох повторних за формулами (5.1.1), (5.1.2):
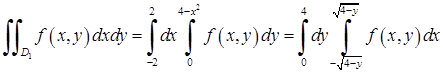 .
.
б) Знайдемо масу пластини 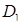 за формулою (5.1.8) (де густина маси
за формулою (5.1.8) (де густина маси 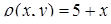 ):
):  . Спочатку обчислимо за змінною
. Спочатку обчислимо за змінною 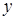 “внутрішній” інтеграл, в якому
“внутрішній” інтеграл, в якому 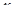 вважається сталим:
вважається сталим:
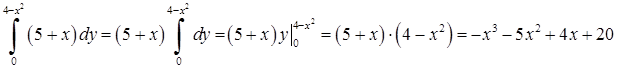 .
.
Тоді 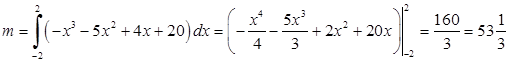 .
.
в) Об’єм циліндричного тіла (обмеженого зверху площиною 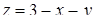 ) згідно (5.1.7):
) згідно (5.1.7): 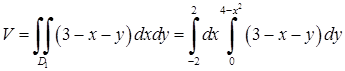 . “Внутрішній” інтеграл
. “Внутрішній” інтеграл

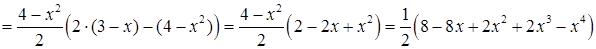 .
.
Значить, 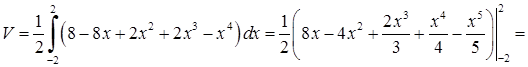
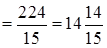 (куб. од.)
(куб. од.)
г) Знайдемо масу циліндричного тіла за формулою (5.1.12):
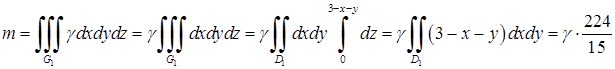 .
.
Зауважимо, що приклад 5.1.2 відповідає завданню 5.1 контрольної роботи.
Література: [1, с. 470 ‑ 492], [2, с. 581 ‑ 616], [3, с. 494 – 499], [13].
Криволінійні інтеграли
Для обчислення криволінійних інтегралів по координатах (інтегралів другого роду), тобто інтегралів виду 
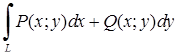 , (5.2.1)
, (5.2.1)
використовується одна із формул:
· якщо крива задана рівнянням виду 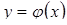 і при переміщенні із точки
і при переміщенні із точки  цієї кривої в точку змінюється від до , то
цієї кривої в точку змінюється від до , то
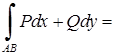
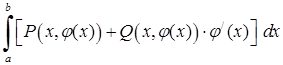 ; (5.2.2)
; (5.2.2)
· якщо крива задана параметрично, тобто системою рівнянь , і при переміщенні із точки в точку параметр змінюється від до , то
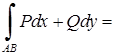
 . (5.2.3)
. (5.2.3)
В процесі обчислення криволінійних інтегралів по довжині дуги (інтегралів першого роду) користуються однією із формул:
|
|
|
· якщо крива задана рівнянням виду 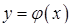
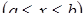 , то
, то  ,
,
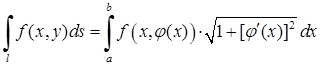 . (5.2.4)
. (5.2.4)
· якщо крива задана параметрично, тобто системою 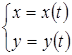 , де
, де 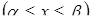 , то
, то 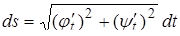 , і
, і
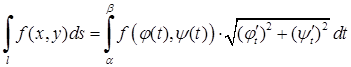 . (5.2.5)
. (5.2.5)
Значення криволінійного інтеграла другого роду при зміні напряму руху вздовж кривої змінюється на протилежне, а інтеграл першого роду не залежить від напряму.
Криволінійні інтеграли у просторі визначаються аналогічно.
Приклад 5.2.1. Обчислити криволінійні інтеграли: 1) 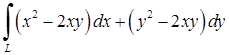 , де – дуга параболи
, де – дуга параболи 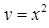 , що пробігається від точки до точки ; 2)
, що пробігається від точки до точки ; 2) 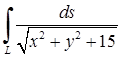 , де
, де 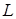 – відрізок прямої, що з’єднує точки О(0; 0) і А(1; 2); 3)
– відрізок прямої, що з’єднує точки О(0; 0) і А(1; 2); 3) 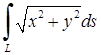 , де
, де 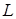 – дуга кривої, заданої параметрично:
– дуга кривої, заданої параметрично: 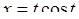 ,
, 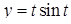 ,
,  .
.
Розв’язання. 1) В цей інтеграл другого роду підставимо 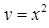 ,
, 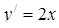 ,
, 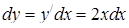 і врахуємо, що змінюється від –1 до 1 при русі з точки до точки . Тоді згідно (5.2.2) маємо:
і врахуємо, що змінюється від –1 до 1 при русі з точки до точки . Тоді згідно (5.2.2) маємо:
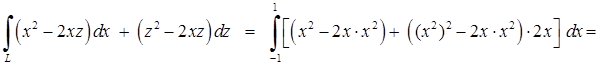
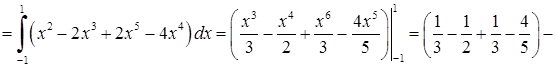
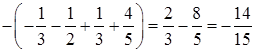 .
.
2) Рівняння прямої, що з’єднує точки О(0; 0) і А(1; 2), має вид  ,
,  змінюється від 0 до 1 при русі від точки О до точки А,
змінюється від 0 до 1 при русі від точки О до точки А, 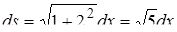 . Значить, інтеграл першого роду дорівнює згідно (5.2.4):
. Значить, інтеграл першого роду дорівнює згідно (5.2.4): 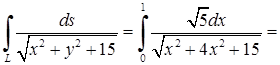
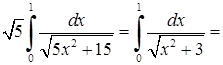
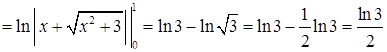 .
.
3) 
Значить, інтеграл першого роду дорівнює згідно (5.2.5): 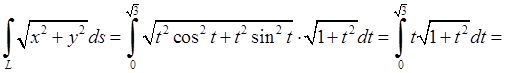
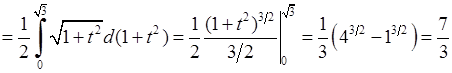 .
.
Зауважимо, що приклад 5.2.1 відповідає завданню 5.2 контрольної роботи.
Література: [1, с. 458 ‑ 467], [2, с. 617 ‑ 625], [3, с. 499 – 502], [14].
МОДУЛЬ 6
ЧИСЛОВІ І СТЕПЕНЕВІ РЯДИ
Числові ряди
Числовий ряд
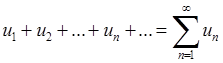 (6.1.1)
(6.1.1)
збігається (має суму 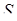 ), якщо
), якщо
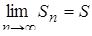 , (6.1.2)
, (6.1.2)
( 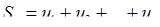 – послідовність часткових сум).
– послідовність часткових сум).
Для всіх збіжних і деяких розбіжних рядів виконується необхідна умова збіжності (достатня ознака розбіжності):
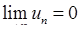 . (6.1.3)
. (6.1.3)
Якщо 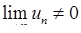 (необхідна умова не виконується), то такий ряд обов’язково розбігається. Якщо ж
(необхідна умова не виконується), то такий ряд обов’язково розбігається. Якщо ж 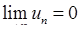 , то ряд може як збігатися, так і розбігатися.
, то ряд може як збігатися, так і розбігатися.
В науці і практиці часто потрібне знання не суми ряду, а лише факту збіжності ряду (або його розбіжності). Для цього застосовуються достатні ознаки збіжності.
Ознака порівняння: якщо (починаючи з деякого номера 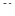 ) для двох рядів виконується
) для двох рядів виконується 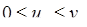 , то
, то
· якщо збігається ряд з загальним членом 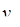 , то збігається ряд з загальним членом
, то збігається ряд з загальним членом 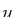 ;
;
· якщо розбігається ряд з загальним членом 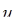 , то розбігається ряд з загальним членом
, то розбігається ряд з загальним членом 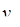 .
.
Гранична ознака порівняння: якщо для знакододатних рядів 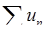 і
і 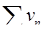 виконується умова
виконується умова
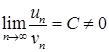 , (6.1.4)
, (6.1.4)
то обидва ряди збігаються або розбігаються одночасно.
При застосуванні ознак порівняння використовують “еталонні” ряди, умови збіжності або розбіжності яких відомі, наприклад, так званий узагальнений гармонійний ряд  (де р – число).
(де р – число).
Ознака Даламбера. Якщо для знакододатного ряду 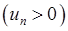 існує
існує
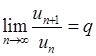 (6.1.5)
(6.1.5)
(границя відношення наступного члена до попереднього), то
· якщо 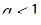 , то ряд збігається;
, то ряд збігається;
· якщо 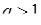 , то ряд розбігається;
, то ряд розбігається;
· якщо 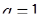 , то про збіжність (розбіжність) ряду нічого сказати не можна (слід скористатися іншими ознаками збіжності рядів).
, то про збіжність (розбіжність) ряду нічого сказати не можна (слід скористатися іншими ознаками збіжності рядів).
Цю ознаку рекомендується використовувати, якщо загальний член досліджуваного ряду містить показникові або факторіальні елементи відносно номера 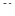 .
.
Радикальна ознака Коші. Якщо для ряду, загальний член якого 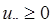 , існує
, існує
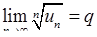 , (6.1.6)
, (6.1.6)
То
· якщо 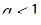 , то ряд збігається;
, то ряд збігається;
· якщо 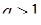 , то ряд розбігається;
, то ряд розбігається;
· якщо 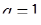 , то про збіжність (розбіжність) ряду нічого сказати не можна (слід скористатися іншими ознаками збіжності рядів).
, то про збіжність (розбіжність) ряду нічого сказати не можна (слід скористатися іншими ознаками збіжності рядів).
Дану ознаку рекомендується застосовувати, якщо загальний член ряду є показниково-степеневою функцією відносно 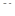 .
.
Інтегральна ознака Коші. Якщо функція 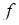 ‑ неперервна, є незростаючою і
‑ неперервна, є незростаючою і 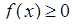 при
при 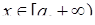 (де
(де 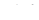 ), то ряд
), то ряд 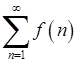 збігається або розбігається одночасно з невласним інтегралом
збігається або розбігається одночасно з невласним інтегралом  .
.
Умовам цієї ознаки до функції 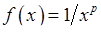 задовольняє узагальнений гармонійний ряд
задовольняє узагальнений гармонійний ряд 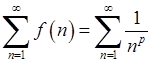 . Через те, що невласний інтеграл
. Через те, що невласний інтеграл 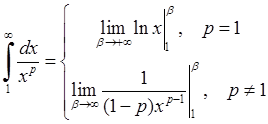 =
= 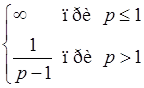 ,
,
то ряд  збігається при
збігається при 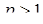 , і розбігається при
, і розбігається при 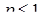 .
.
Збіжність знакопереміжних числових рядів 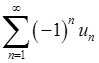 досліджують за ознакою Лейбніца. Якщо
досліджують за ознакою Лейбніца. Якщо
· розпочинаючи з деякого номера, члени ряду, взяті за абсолютним значенням, зменшуються при зростанні їх номера 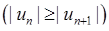 ;
;
· 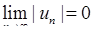 ,
,
то ряд збігається.
Приклад 6.1.1. Дослідити на збіжність числові ряди: 1) 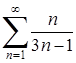 , 2)
, 2) 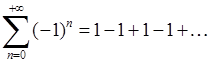 , 3)
, 3) 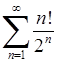 , 4)
, 4) 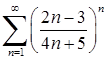 , 5)
, 5) 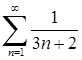 , 6)
, 6) 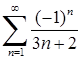 .
.
Розв’язання. 1) Обчислимо границю загального члена 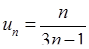 ряду:
ряду: 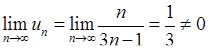 . Ряд
. Ряд 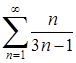 розбігається, бо необхідна умова збіжності (6.1.3) не виконується.
розбігається, бо необхідна умова збіжності (6.1.3) не виконується.
2) Границя загального члена ряду 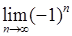 не існує, тобто необхідна умова збіжності (6.1.3) не виконується. Значить, ряд
не існує, тобто необхідна умова збіжності (6.1.3) не виконується. Значить, ряд 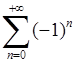 розбігається.
розбігається.
3) Ряд 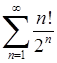 є знакододатним, бо загальний член ряду
є знакододатним, бо загальний член ряду 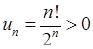 (факторіал
(факторіал 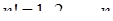 , див. також розділ 8). Наступний член
, див. також розділ 8). Наступний член 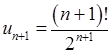 , відношення наступного члена до попереднього
, відношення наступного члена до попереднього 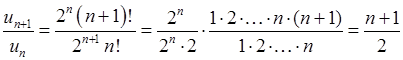 . Тоді границя (6.1.5):
. Тоді границя (6.1.5): 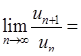
 . Отже, ряд розбігається за ознакою Даламбера.
. Отже, ряд розбігається за ознакою Даламбера.
4) Загальний член ряду 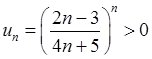 . Значить,
. Значить, 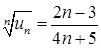 , і границя (6.1.6):
, і границя (6.1.6): 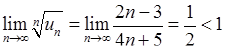 . Отже ряд
. Отже ряд 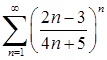 збігається за радикальною ознакою Коші.
збігається за радикальною ознакою Коші.
5) Порівняємо ряд 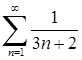 із гармонійним рядом
із гармонійним рядом 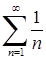 .
.  ;
; 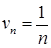 , тоді границя (6.1.4):
, тоді границя (6.1.4): 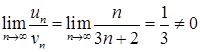 . Отже, за граничною ознакою порівняння досліджуваний ряд розбігається, оскільки гармонійний ряд розбігається за інтегральною ознакою Коші. (Можна було застосувати інтегральну ознаку Коші зразу до вихідного ряду).
. Отже, за граничною ознакою порівняння досліджуваний ряд розбігається, оскільки гармонійний ряд розбігається за інтегральною ознакою Коші. (Можна було застосувати інтегральну ознаку Коші зразу до вихідного ряду).
6) Ряд 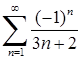 є знакопереміжним. Оскільки
є знакопереміжним. Оскільки 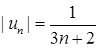 ,
, 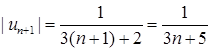 , то
, то 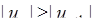 і
і 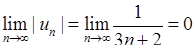 . Отже, досліджуваний ряд збігається за ознакою Лейбніца.
. Отже, досліджуваний ряд збігається за ознакою Лейбніца.
Література: [1, с. 362 ‑ 376], [2, с. 659 ‑ 673], [4, с. 214 – 246], [15].
Степеневі ряди
Степеневий ряд
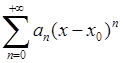 (6.2.1)
(6.2.1)
( 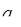 ,
, 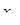 ‑ задані числа) збігається при
‑ задані числа) збігається при 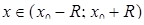 , де
, де 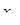 ‑ центр інтервалу (в цій точці ряд набуває вигляду
‑ центр інтервалу (в цій точці ряд набуває вигляду 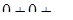 , отже завжди збігається), а
, отже завжди збігається), а 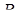 ‑ радіус збіжності
‑ радіус збіжності 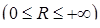 . Для знаходження інтервалу збіжності степеневого ряду можна застосовувати ознаку Даламбера, або радикальну ознаку Коші до знакододатного ряду
. Для знаходження інтервалу збіжності степеневого ряду можна застосовувати ознаку Даламбера, або радикальну ознаку Коші до знакододатного ряду 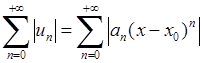 . Наприклад, застосовуючи ознаку Даламбера до цього ряду, отримаємо умову для визначення інтервалу збіжності степеневого ряду (6.2.1):
. Наприклад, застосовуючи ознаку Даламбера до цього ряду, отримаємо умову для визначення інтервалу збіжності степеневого ряду (6.2.1):
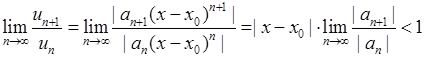 . (6.2.2)
. (6.2.2)
Розв’язуючи цю нерівність відносно  , знаходимо інтервал збіжності
, знаходимо інтервал збіжності 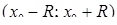 . Множина збіжності або співпадає з цим інтервалом, або є одним із проміжків
. Множина збіжності або співпадає з цим інтервалом, або є одним із проміжків 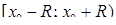 ,
, 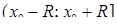 ,
, 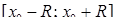 . Якщо степеневий ряд збіжний лише при
. Якщо степеневий ряд збіжний лише при 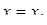 , то його радіус збіжності
, то його радіус збіжності 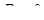 . Якщо ряд збіжний при будь-якому
. Якщо ряд збіжний при будь-якому  , то
, то 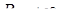 .
.
Степеневі ряди є узагальненням багаточленів і широко застосовуються в науці. Це пов’язано з можливістю представлення багатьох функцій, зокрема всіх елементарних функцій у вигляді сум степеневих рядів, що називаються рядами Тейлора (Маклорена, якщо 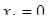 ). Наприклад,
). Наприклад,
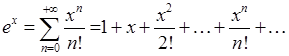 , (6.2.3)
, (6.2.3)
 ,
, 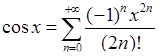 . (6.2.4)
. (6.2.4)
За допомогою розкладу функцій в ряд Тейлора можна з будь-якою точністю обчислити значення функцій, інтегралів, границь і т.д. Саме на цьому грунтуються всі обчислення, що виконуються компьютерами з елементарними та спеціальними функціями.
Приклад 6.2.1. Знайти множину збіжності степеневих рядів: 1) 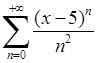 , 2)
, 2) 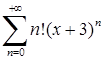 , 3)
, 3) 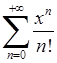 .
.
Розв’язання. 1) Тут 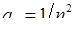 ,
, 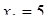 ‑ центр інтервалу збіжності. Оскільки
‑ центр інтервалу збіжності. Оскільки  ,
, 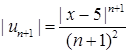 , то (при
, то (при  )
) 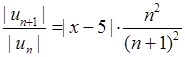 . Значить, за ознакою Даламбера ряд збігається, якщо
. Значить, за ознакою Даламбера ряд збігається, якщо 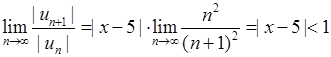 . Тобто, якщо
. Тобто, якщо 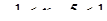 , або
, або 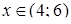 , то степеневий ряд
, то степеневий ряд 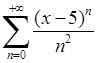 збігається. До того ж за ознакою Даламбера якщо
збігається. До того ж за ознакою Даламбера якщо 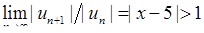 , то ряд розбігається. Залишилось дослідити збіжність ряду на кінцях інтервалу (там, де
, то ряд розбігається. Залишилось дослідити збіжність ряду на кінцях інтервалу (там, де 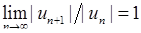 ).
).
При  маємо знакододатний ряд
маємо знакододатний ряд 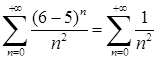 , який збігається за інтегральною ознакою Коші. При
, який збігається за інтегральною ознакою Коші. При  маємо знакопереміжний ряд
маємо знакопереміжний ряд  , який збігається за ознакою Лейбніца. Таким чином, множина збіжності ряду являє собою відрізок
, який збігається за ознакою Лейбніца. Таким чином, множина збіжності ряду являє собою відрізок 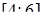 . Тобто ряд
. Тобто ряд 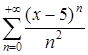 збігається, якщо
збігається, якщо 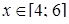 , і розбігається, якщо
, і розбігається, якщо 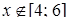 . (Радіус збіжності
. (Радіус збіжності  ).
).
2) Тут 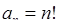 ,
, 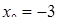 . Оскільки
. Оскільки 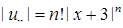 ,
, 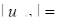
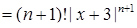 , то (при
, то (при 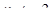 )
) 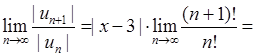
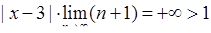 . Отже, за ознакою Даламбера ряд
. Отже, за ознакою Даламбера ряд 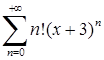 розбігається при всіх
розбігається при всіх 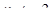 , а збігається лише в точці
, а збігається лише в точці 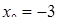 . (Радіус збіжності
. (Радіус збіжності 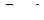 ).
).
3) Тут 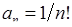 ,
, 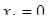 . Оскільки
. Оскільки 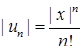 ,
,  , то (при
, то (при  )
) 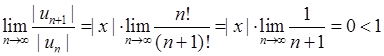 . Отже за ознакою Даламбера ряд
. Отже за ознакою Даламбера ряд 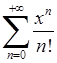 збігається при всіх
збігається при всіх 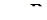 . (Радіус збіжності
. (Радіус збіжності 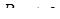 ).
).
Література: [1, с. 377 ‑ 380], [2, с. 626 ‑ 676], [4, с. 247 – 262], [15].
МОДУЛЬ 7
Дата добавления: 2018-09-22; просмотров: 307; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
