I. Анализ результатов контрольной работы.
II. Изучение нового материала.
1. Устно решить задачу № 254
2. Решить задачу № 255 на доске и в тетрадях.

| Дано:  СDЕ; СD = DЕ; СF СDЕ; СD = DЕ; СF  DЕ; DЕ;
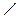 D = 54°.
Найти: D = 54°.
Найти: 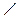 ЕСF.
Решение
По условию треугольник СDЕ – равнобедренный, тогда ЕСF.
Решение
По условию треугольник СDЕ – равнобедренный, тогда 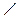 Е = Е = 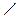 DСЕ = (180° – 54°) : : 2 = 63° (углы при основании равнобедренного треугольника равны). DСЕ = (180° – 54°) : : 2 = 63° (углы при основании равнобедренного треугольника равны).
|
Так как СF  DЕ по условию, то треугольник СFЕ – прямоугольный, в нем
DЕ по условию, то треугольник СFЕ – прямоугольный, в нем 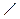 CFЕ = 90°,
CFЕ = 90°, 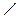 Е = 63°; тогда
Е = 63°; тогда 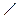 ЕСF = 180° – (90° + 63°) = 27°.
ЕСF = 180° – (90° + 63°) = 27°.
Ответ: 27°.
3. Рассмотреть свойство 1°
4. Доказательство свойств 2° и 3°
| Теорема | Обратная теорема | |
| Дано | DАВС; ÐА = 90° ÐВ = 30° | DАВС; ÐА = 90°,
АС =  ВС ВС
|
| Доказать | АС =  ВС ВС
| ÐВ = 30° |
III. Закрепление изученного материала.
1. Устно решить задачи по готовым чертежам на доске:


Рис. 1 Рис. 2
1) Дано:  АВС (рис. 1).
АВС (рис. 1).
Найти: углы  АВС.
АВС.
2) Дано: а || b (рис. 2).
Найти: углы треугольника MON.
2. Решить задачу № 257 на доске и в тетрадях.
 Рис. 3
Рис. 3
| Дано:  АВС (рис. 3); АВС (рис. 3); 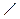 C = 90°, C = 90°,
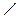 ВАD = 120° внешний угол;
АС + АВ = 18 см.
Найти: АС и АВ. ВАD = 120° внешний угол;
АС + АВ = 18 см.
Найти: АС и АВ.
|
Решение
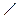 CАВ = 180° – 120° = 60° (смежные углы), тогда
CАВ = 180° – 120° = 60° (смежные углы), тогда  В = 90° – 60° =
В = 90° – 60° =
= 30° (по свойству 1°); АС =  АВ (свойство 2°; катет, лежащий против угла в 30°).
АВ (свойство 2°; катет, лежащий против угла в 30°).
По условию АС + АВ = 18 см;  АВ + АВ = 18 см; 1
АВ + АВ = 18 см; 1  АВ = 18 см, АВ = 12 см; значит, АС = 18 – 12 = 6 (см).
АВ = 18 см, АВ = 12 см; значит, АС = 18 – 12 = 6 (см).
Ответ: АВ = 12 см; АС = 6 см.
3. Решить задачу № 260.
 Рис. 4
Рис. 4
| Дано:  DМС (рис. 4); DМ = МС; МО DМС (рис. 4); DМ = МС; МО  DС; DМ = 15,2 см; МО = 7,6 см.
Найти: углы DС; DМ = 15,2 см; МО = 7,6 см.
Найти: углы  DМС.
Решение
Так как МО = DМС.
Решение
Так как МО =  DМ, то по свойству 3° DМ, то по свойству 3°  D = 30°, тогда D = 30°, тогда  С = 30°, С = 30°,  М = = 180° – (30° + 30°) = 180° – 60° = 120°. М = = 180° – (30° + 30°) = 180° – 60° = 120°.
|
Ответ: 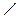 D =
D =  С = 30°;
С = 30°;  М = 120°.
М = 120°.
IV. Итоги урока.
Домашнее задание: изучить п. 34; повторить пункты 15–33; ответить на вопросы 10 и 11 на с. 90; решить №№ 256, 259.
Урок 39
ПРИЗНАКИ РАВЕНСТВА ПРЯМОУГОЛЬНЫХ
ТРЕУГОЛЬНИКОВ
Цели: доказать признаки равенства прямоугольных треугольников и показать, как они применяются при решении задач.
Ход урока
I. Повторение изученного материала.
1. Сформулировать свойства прямоугольных треугольников.
2. Вспомнить признаки равенства треугольников.
3. Решить задачу: гипотенузы ВD и АС прямоугольных треугольников АВD и АВС с общим катетом АВ и с равными катетами АD и ВС пересекаются в точке О (см. рис.). Докажите, что треугольник АОВ равнобедренный.

II. Изучение нового материала.
1. Самостоятельно (устно), используя признаки равенства треугольников, доказать признаки равенства прямоугольных треугольников по двум катетам, по катету и прилежащему острому углу, по гипотенузе и острому углу
2. Доказательство признака равенства прямоугольных треугольников по гипотенузе и острому углу (устно) по моделям равных прямоугольных треугольников.
3. Доказательство признака равенства прямоугольных треугольников по гипотенузе и катету.
III. Закрепление изученного материала.
1. Решить задачу № 261 на доске и в тетрадях.

| Дано:  АDС; АD = DС;
АВ и СK – высоты.
Доказать: АВ = СK. АDС; АD = DС;
АВ и СK – высоты.
Доказать: АВ = СK.
|
Доказательство
По условию АВ  DС и СK
DС и СK  АD, тогда
АD, тогда  АВС и
АВС и  АKС – прямоугольные; в них АС – общая гипотенуза и
АKС – прямоугольные; в них АС – общая гипотенуза и  KАС =
KАС =  ВСА, так как по условию
ВСА, так как по условию  АDС равнобедренный.
АDС равнобедренный.
Значит,  АВС =
АВС =  СKА (по гипотенузе и острому углу).
СKА (по гипотенузе и острому углу).
Тогда АВ = СK.
3. Решить задачу № 269 на доске и в тетрадях.
Указание: при решении задачи применить вывод задачи № 268 – признак равенства прямоугольных треугольников по катету и противолежащему углу.
IV. Итоги урока.
Домашнее задание: изучить п. 35; ответить на вопросы 12–13 на с. 90; решить задачи №№ 262, 264.
Урок 40
ПРИЗНАКИ РАВЕНСТВА ПРЯМОУГОЛЬНЫХ
ТРЕУГОЛЬНИКОВ
Цели: научить применять признаки равенства прямоугольных треугольников и их свойства при решении задач; вырабатывать умение решать задачи; учить логически мыслить.
Ход урока
I. Устная работа.
1. Сформулировать свойства прямоугольных треугольников.
2. Сформулировать признаки равенства прямоугольных треугольников.
3. Устно решить задачи по готовым чертежам:
1) На рисунке 1 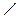 В =
В = 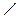 С = 90°;
С = 90°; 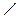 1 =
1 = 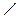 2. Докажите, что АВ = СD.
2. Докажите, что АВ = СD.
2) На рисунке 2 АВ = СD; ВС = АD, 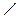 АFВ =
АFВ =  СЕD = 90°. Докажите, что BF = ED; АF = EC.
СЕD = 90°. Докажите, что BF = ED; АF = EC.
3) На рисунке 3 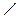 1 =
1 = 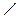 2 = 90°, АВ = DС. Докажите, что ВС = АD.
2 = 90°, АВ = DС. Докажите, что ВС = АD.
4) На рисунке 4 АН и А1Н1 – высоты треугольников АВС и А1В1С1; АС = А1С1;  1 =
1 =  2; АН = А1Н1.
2; АН = А1Н1.
Докажите, что  АВС =
АВС =  А1В1С1.
А1В1С1.


Рис. 1 Рис. 2


Рис. 3 Рис. 4
II. Решение задач.
1. Решить задачу № 263 на доске и в тетрадях.
2. Решить задачу № 267 на доске и в тетрадях.
Указание: при доказательстве применить признак равенства прямоугольных треугольников по гипотенузе и катету.
III. Самостоятельная работа (проверочного характера) (20 мин).
Вариант I
1. На рисунке 5 АD = DС; ЕD = DF; 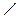 1 =
1 =  2 = 90°. Докажите, что треугольник АВС равнобедренный.
2 = 90°. Докажите, что треугольник АВС равнобедренный.
2. Один из углов прямоугольного треугольника равен 60°, а сумма гипотенузы и меньшего катета равна 18 см. Найдите гипотенузу и меньший катет.
Вариант II
1. На рисунке 6  1 =
1 =  2,
2,  3 =
3 =  4 = 90°; ВD = DС. Докажите, что треугольник АВС равнобедренный.
4 = 90°; ВD = DС. Докажите, что треугольник АВС равнобедренный.
2. Один из острых углов прямоугольного треугольника в два раза меньше другого, а разность гипотенузы и меньшего катета равна 15 см. Найдите гипотенузу и меньший катет.
Вариант III (для более подготовленных учащихся)
1. Через середину отрезка АВ проведена прямая а. Из точек А и В к прямой а проведены перпендикуляры АС и ВD. Докажите, что АС = ВD.
2. В прямоугольном треугольнике СDЕ с прямым углом Е проведена высота EF. Найдите CF и FD, если СD = 18 см, а  DСЕ = 30°.
DСЕ = 30°.
Вариант IV (для более подготовленных учащихся)
1. Из точки М биссектрисы неразвернутого угла О проведены перпендикуляры МА и МВ к сторонам этого угла. Докажите, что МА = МВ.
2. В прямоугольном треугольнике АВС с гипотенузой АВ и 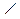 А = 60° проведена высота СН. Найдите ВН, если АН = 6 см.
А = 60° проведена высота СН. Найдите ВН, если АН = 6 см.


Рис. 5 Рис. 6
IV. Итоги урока.
Домашнее задание: повторить пункты 30–35; подготовиться к устному опросу по карточкам; прочитать п. 36; решить №№ 258, 265.
Урок 43
решение задач по теме «ПРЯМОУГОЛЬНые ТРЕУГОЛЬНИКи»
Цели: повторить и систематизировать ранее изученный материал; вырабатывать навыки в решении задач; развивать логическое мышление учащихся.
Ход урока
Дата добавления: 2018-09-20; просмотров: 387; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
