Законы распределения дискретных и непрерывных случайных величин. Понятие закона распределения вероятностей дискретной случайной величины

⇐ ПредыдущаяСтр 9 из 11Следующая ⇒

Может показаться, что для задания дискретной случайной величины достаточно перечислить все ее возможные значения. Но случайная величина может принимать различные значения с различной вероятностью. Поэтому для задания (описания) случайной величины нужно задать не только ее возможные значения, но вероятности, с которыми принимается то или иное значение случайной величины. Дискретная случайная величина задается законом распределения вероятностей, а встречная случайная величина – функцией распределения вероятностей.

Биномиальное распределение

Пусть производится п независимых испытаний, в каждом из которых событие А может появиться, либо не появиться. Вероятность наступления события А во всех испытаниях одинакова и равна р (следовательно, вероятность не наступления 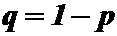). Рассмотрим дискретную величину Х – число появлений события А в п испытаниях.

Поставим задачу: найти закон распределения величины Х, т.е. нужно найти все возможные значения случайной величины и вероятности появления этих значений.

Очевидно, событие А в п испытаниях может не появиться , либо появиться один раз , либо два раза , , либо п раз .

По формуле Бернулли

(1)

где . Формула (1) является аналитическим выражением искомого закона распределения. Она справедлива при и , т.к.

Определение. Биномиальным называют распределение вероятностей, определяемое формулой Бернулли.

Напишем биномиальный закон распределения вероятностей в виде таблицы:

Х	0	1		k			n
P

Для биномиального закона

Пример. Вероятность брака в данной партии деталей . Какова вероятность того, что в партии из трех деталей будет бракованных деталей?

Решение. , т.к. ;

;

Х	0	1	2	3
Р	0,729	0,243	0,027	0,001

Распределение Пуассона

Пусть производится п независимых испытаний, в каждом из которых вероятность появления события А равна р.

Применима формула Бернулли. Но если п – велико, то ей пользоваться неудобно. В случаях, когда п – велико, р – мало, прибегают к асимптотической формуле Пуассона.

Итак, поставим своей задачей найти вероятность того, что при очень большом числе испытаний, в каждом из которых вероятность наступления события очень мала, событие наступит ровно k раз, т.е. найдем .

Сделаем важное допущение: произведение сохраняет постоянное значение, а именно:

(это означает, что среднее число появлений события в различных сериях испытаний, т.е. при различных значениях п, остается неизменным).

По формуле Бернулли:

Так как , то .

Поскольку п – велико, то вместо найдем .

Итак,

это закон распределения Пуассона вероятностей массовых (п – велико) редких ( мало) событий.

Замечание. Есть специальные таблицы, пользуясь которыми можно по известным k и найти .

Для закона Пуассона

Пример. Аппаратура содержит 5000 элементов, вероятность отказа каждого из них . Найти вероятность отказа аппаратуры, если она отказывает при отказе хотя бы одного из элементов.