Непрерывные случайные величины.
Функция распределения и плотность распределения вероятностей
Наряду с дискретными случайными величинами, принимающими конечное или счетное множество значений в теории вероятностей широко используются непрерывные случайные величины. Множество непрерывной случайной величины несчетно и обычно представляет собой некоторый промежуток.
Определение. Случайная величина Х называется непрерывной, если существует неотрицательная функция  такая, что для каждого хфункцию распределения непрерывной случайной величины Хможно представить в виде
такая, что для каждого хфункцию распределения непрерывной случайной величины Хможно представить в виде
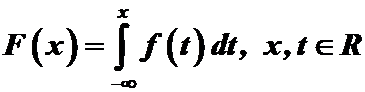 .
.
Свойства функции распределения непрерывной случайной величины
1. 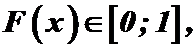 т.е.
т.е. 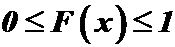 ;
;
2.  есть непрерывная, неубывающая функция;
есть непрерывная, неубывающая функция;
3. 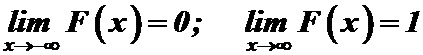 .
.
Определение. Плотностью распределения непрерывной случайной величины называется первая производная от функции распределения:
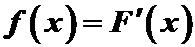 .
.
Свойства плотности
1. Плотность распределения неотрицательна, т.е. 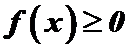 .
.
2. Несобственный интеграл от плотности распределения по всей числовой прямой равен единице:  .
.
Непрерывная случайная величина считается заданной, если задана ее функция распределения или плотность распределения вероятностей. При этом функция распределения  называется интегральным законом, а плотность распределения – дифференциальным законом распределения.
называется интегральным законом, а плотность распределения – дифференциальным законом распределения.
Вероятность того, что случайная величина Х примет значения из интервала 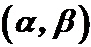 находится по формуле:
находится по формуле:
 .
.
Примечание.Интервал для возможных значений непрерывной случайной величины Х может быть и замкнутым, т.е.
|
|
|
 .
.
Пример 1. Дана функция распределения непрерывной случайной величины Х:
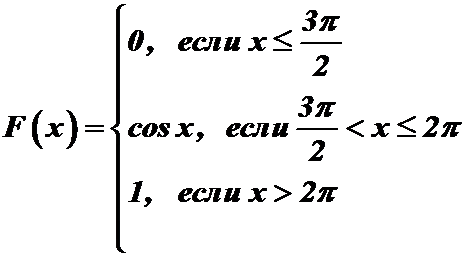 .
.
Найти плотность распределения непрерывной случайной величины Хи построить графики функции распределения и плотности распределения. Определить вероятность того, что Х попадет в интервал 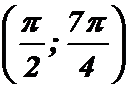 .
.
Решение. Плотность распределения равна первой производной от функции распределения:
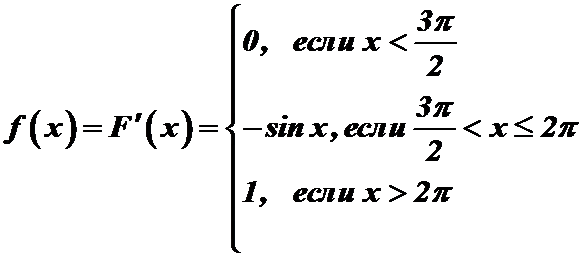 .
.
Графики функции распределения и плотности распределения представлены на рисунках 4 и 5.
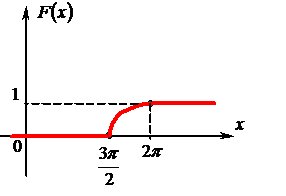
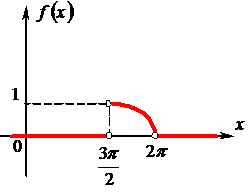
Рис. 4 Рис. 5
Вероятность того, что Х попадает в интервал 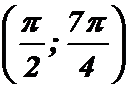 , найдем по формуле:
, найдем по формуле:
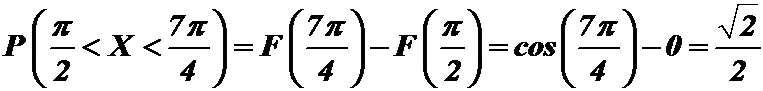 .
.
Пример 2. Задана плотность распределения непрерывной случайной величины Х:
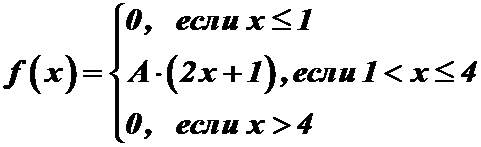 .
.
Найти коэффициент А, функцию распределения непрерывной случайной величины и вероятность того, что Х примет значение, принадлежащее интервалу  .
.
Решение. Для нахождения константы А воспользуемся свойством плотности  .
.
Тогда для заданной непрерывной случайной величины Х:
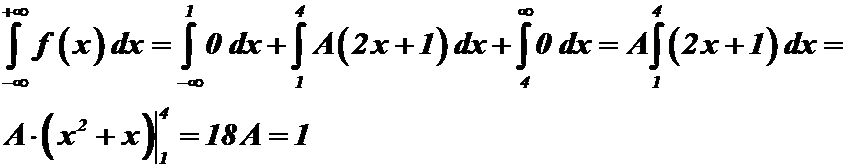 .
.
Получаем 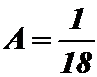 , а плотность распределения имеет вид:
, а плотность распределения имеет вид:
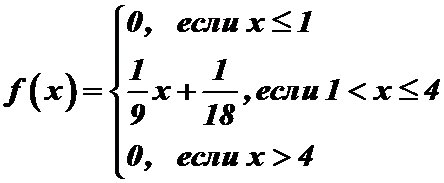 .
.
Для отыскания функции распределения воспользуемся формулой:
 .
.
Если 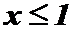 , то
, то  , следовательно
, следовательно 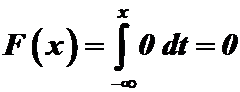 .
.
|
|
|
Если 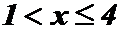 , то
, то  и
и
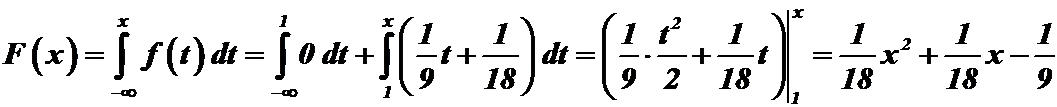 .
.
Если 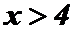 , то
, то  и
и
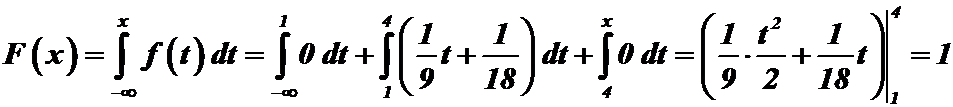 .
.
Итак, искомая функция распределения:
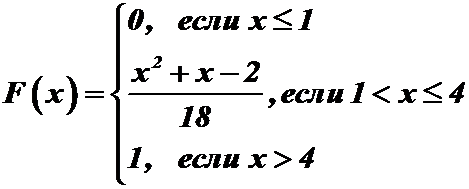 .
.
Вероятность того, что Х примет значение, принадлежащее интервалу  , найдем по формуле:
, найдем по формуле:


Среди непрерывных случайных величин наиболее распространены случайные величины, подчиняющиеся нормальному, равномерному и показательному законам.
Дата добавления: 2018-08-06; просмотров: 222; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
