Свойства определителей.. № 03.(Два одинаковых столбца или строки)
Если две строки (столбца) матрицы равны между собой, то определитель этой матрицы равен нулю.
Доказательство. По Свойству 3, при перестановке двух строк местами определитель изменяет свой знак. С другой стороны, перестановка местами одинаковых строк не изменяет определитель. Следовательно, det A = –det A, что влечет det A = 0.
21. Общее число произведений в разложении определителя
Всего существует три порядка определителей:
1-го порядка - прои-й нет, т.к. определитель 1го порядка равен единственному эл-ту матрицы (т.к. она 1х1)
2-го порядка - два произведения.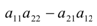 
3-го порядка - в завис-ти от метода разложения. 1) Разлож-е по стр/стлб - 3 произвед-я. 2) Метод звездочки - 6 произ-й. 3) Метод паралл. прямых - 6 произ-й.
22. Рекурсивная формула выражения определителя N-го порядка через определители (N-1)-го порядка (по строке)
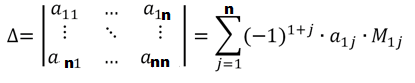
23. Количество шагов,необходимых для вычисления определителя N-го порядка
Для вычисления опр-ля n-го порядка необходимо:
1) Знать формулу раскрытия определителя по стр/стлб:
2) Найти по формуле алгебраическое дополнение для каждого элемента, участвующего в вычислении:
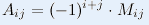
3) Найденные алг. дополнения подставляем в исх. формулу и вычисляем ответ
24. Метод Гаусса вычисления определителя N-го порядка
Для вычисления определителя n-го порядка методом Гаусса необходимо:
1) Привести матрицу к треугольному виду (нули ниже главной диагонали)
2) Перемножить элементы гл. диагонали
3) Посмотреть, нужно ли менять знак опр-теля (если строки местами не меняли, то нет)
ПРИМЕР?
25.Определитель единичной матрицы
Определитель единичной матрицы всегда равен единице. Это можно элементарно доказать, взяв ед. матр. и вычислив ее опр-ль. Ед. матр. - матр., в которой на гл. диаг. лежат ед-цы, а ост. эл-ты - нули. (Также можно отметить, что ед. матр., в свою очередь, играет роль единицы в алгебре)
26.Определитель диагональной матрицы
Определитель диаг. матр. равен произвед-ю диаг. элементов. Диаг. матр. - матр., все эл-ты которой, кроме гл.диаг, равны нулю.
27. Определитель верхнетреугольной матрицы
Опр-тель треугольной матрицы (и верх., и ниж.) равен произвед-ю элементов на её гл. диагонали. Верхнетреуг. матр. - квадр. матр., в которой все эл-ты ниже гл. диагонали равны нулю.
28. Определитель нижнетреугольной матрицы
Опр-тель треугольной матрицы (и верх., и ниж.) равен произвед-ю элементов на её гл. диагонали. Нижнетреуг. матр. - квадр. матр., в которой все эл-ты выше гл. диагонали равны нулю.
29. Формула разложения определителя 1-го порядка
∆ = |a11| = a11. Она выглядит так потому, что при определителе 1-го порядка нам дана матрица 1х1.
30. Определитель 1-го порядка как решение СЛАУ 1-го порядка
Определитель 1-го порядка в СЛАУ 1го порядка равен решению этого СЛАУ, т.к. является непосред-но равным единств. эл-ту данной системы. (при 1 порядке ед.эл-т=опр-лю=реш-ю СЛАУ)
31. Формула разложения определителя 2-го порядка
|
|
|
|
|
|
Определителем 2-го порядка называют число, представленное в виде специальной конструкции: d=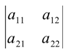 
, которой ставят в соответствие число 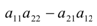. Записывают:
d= =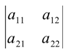
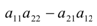
32. Определитель 2-го порядка как решение СЛАУ 2-го порядка
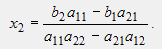(x1=b1a22-b2a12/∆2; x2=b2a11-b1a21/∆ (на всякий))
33. Формула разложения определителя 3-го порядка
Разложение по любой стр./стлб.
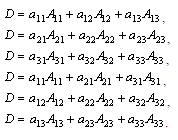
34. Определитель 3-го порядка как решение СЛАУ 3-го порядка
Опр-ль помогает узнать, сколько решений с СЛАУ. И если опр-ль не =0, то система имеет единственное решение. Находим главный опр-ль одним из способов (Звездочка, паралл. прямые, разложение по стр/стлб), а потом находим вспомогательные. После делим каждый вспом. на главный и получаем корни, являющиеся решением.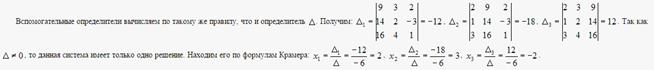 
35. Метод звездочки разложения определителя 3-го порядка
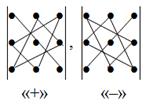
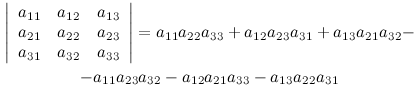
36. Метод параллельных прямых разложения определителя 3-го порядка
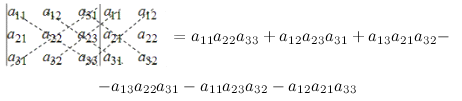
Дата добавления: 2018-08-06; просмотров: 386; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!