Вычисление обратной матрицы с помощью присоединенной матрицы(метод Крамера)
Рассмотрим систему уравнений 
На первом шаге вычислим определитель 
, его называют главным определителем системы.
Если 
, то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса.
Если 
, то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
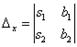и 
На практике вышеуказанные определители также могут обозначаться латинской буквой 
.
Корни уравнения находим по формулам:
, 
Пример:
Решить систему по формулам Крамера. Ответ представить в обыкновенных неправильных дробях. Сделать проверку.
Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).
Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:
Находим главный определитель системы:
Если 
, то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса.
Если 
, то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, 
, 
И, наконец, ответ рассчитывается по формулам:
Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов 
последовательно «прогуливается» слева направо по столбцам главного определителя.
|
|
|
Определение минора к-го порядка.
Минор К-ого порядка матрицы – определитель матрицы, составленный из элементов данной матрицы, стоящих на пересечении произвольно выделенных ее k строк и k столбцов с сохранением их порядка, т.е. минор k-го порядка есть определитель квадратной матрицы размера k x k.
Определение ранга матрицы через наивысший порядок минора.
Минором k-ого порядка матрицы А называется определитель квадратной матрицы порядка 
, составленной из элементов матрицы А, которые находятся в заранее выбранных k строках и k столбцах, причем расположение элементов матрицы А сохраняется.
Ранг матрицы – это наивысший порядок минора матрицы, отличного от нуля. Ранг матрицы не может превышать порядка минора.
Пример:
Матрица 2х4. Если начать находить миноры, то наивысший порядок миноров, отличных от нуля, будет равен 2. А в силу того, что ранг матрицы не может превышать наивысший порядок минора, то он будет либо равен минору, либо будет меньше.
Теорема о ранге матрицы при элементарных преобразованиях
Теорема. Элементарные преобразования не изменяют ранг матрицы.
Для доказательства теоремы достаточно убедиться в том, что в результате элементарных преобразований нулевой определитель остается нулевым, а ненулевой – ненулевым.
Перестановка строк или столбцов матрицы изменяет только знак определителя.
При умножении строки (столбца) матрицы на ненулевое число определитель умножается на это число.
Определитель не изменяется, если к строке (столбцу) прибавляется другая строка (столбец).
Таким образом, в результате элементарных преобразований сингулярные матрицы остаются сингулярными, а несингулярные – несингулярными. (Вырожденной, или сингулярной, или особой, называют квадратную матрицу A, определитель \det(A) которой равен нулю.)
|
|
|
Эквивалентные матрицы.
Такие матрицы А и В, где одна из них получается из другой с помощью элементарных преобразований А э.п В
Канонический вид матрицы.
| 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 |
А =
Дата добавления: 2018-08-06; просмотров: 459; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!