Антиперестановочность произведения матриц
A*B не равно B*A, Т.е умножение матрицы "Слева" не равно умножению матрицы "Справа" на другую матрицу.
Умножение матрицы на матрицу слева. Умножение матрицы на матрицу справа
В произведения A⋅B матрицу A называют левым множителем для B и говорят об умножении матрицы B на матрицу A слева. Аналогично матрицу B называют правым множителем для A и говорят об умножении матрицы A на матрицу B справа. Таким образом, умножение матрицы на некоторую вспомогательную матрицу слева равносильно линейному комбинированию строк матрицы, умножение справа — линейному комбинированию столбцов.
Условие перестановочности умножения матриц
В общем случае 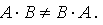 . Если
. Если 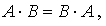 то матрицы А и В называются перестановочными по отношению друг к другу.
то матрицы А и В называются перестановочными по отношению друг к другу.






Возведение матрицы в степень.
Пусть k – целое неотрицательное число. Для любой квадратной матрицы An×n имеем:
Ak=(A⋅A⋅…⋅A) kраз
При этом полагаем, что A0=E, где E – единичная матрица соответствующего порядка.
Пример №4
Задана матрица A=(1−12−3). Найти матрицы A2 и A6.
Решение
Согласно определению A2=A⋅A, т.е. для нахождения A2 нам просто нужно умножить матрицу A саму на себя. Операция умножения матриц рассматривалась в первой части темы, поэтому тут просто запишем процесс решения без подробных пояснений:
A2=A⋅A=(1−12−3)⋅(1−12−3)=(1⋅1+2⋅(−1)−1⋅1+(−3)⋅(−1)1⋅2+2⋅(−3)−1⋅2+(−3)⋅(−3))=(−12−47).
|
|
|
Чтобы найти матрицу A6 у нас есть два варианта. Вариант первый: банально продолжить домножать A2 на матрицу A:
A6=A2⋅A⋅A⋅A⋅A.
Однако можно пойти несколько более простым путём, используя свойство ассоциативности умножения матриц. Расставим скобки в выражении для A6:
A6=A2⋅A⋅A⋅A⋅A=A2⋅(A⋅A)⋅(A⋅A)=A2⋅A2⋅A2.
Если при решении первым способом потребовалось бы четыре операции умножения, то для второго способа – лишь две. Поэтому пойдём вторым путём:
A6=A2⋅A2⋅A2=(−12−47)⋅(−12−47)⋅(−12−47)==(−1⋅(−1)+(−4)⋅22⋅(−1)+7⋅2−1⋅(−4)+(−4)⋅72⋅(−4)+7⋅7)⋅(−12−47)=(−712−2441)⋅(−12−47)==(−7⋅(−1)+(−24)⋅212⋅(−1)+41⋅2−7⋅(−4)+(−24)⋅712⋅(−4)+41⋅7)=(−4170−140239).
Ответ: A2=(−12−47), A6=(−4170−140239).
Транспонированная матрица
Транспонированная матрица — матрица 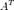 , полученная из исходной матрицы А заменой строк на столбцы.
, полученная из исходной матрицы А заменой строк на столбцы.
Формально, транспонированная матрица для матрицы А размеров  — матрица
— матрица  размеров
размеров  , определённая как
, определённая как 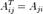 .
.
Например,  и
и 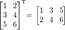
То есть для получения транспонированной матрицы из исходной нужно каждую строчку исходной матрицы записать в виде столбца в том же порядке.
|
|
|
Свойства транспонированных матриц
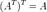 Дважды транспонированная матрица А равна исходной матрице А.
Дважды транспонированная матрица А равна исходной матрице А.
 Транспонированная сумма матриц равна сумме транспонированных матриц.
Транспонированная сумма матриц равна сумме транспонированных матриц.
 Транспонированное произведение матриц равно произведению транспонированных матриц, взятых в обратном порядке.
Транспонированное произведение матриц равно произведению транспонированных матриц, взятых в обратном порядке.
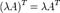 При транспонировании можно выносить скаляр.
При транспонировании можно выносить скаляр.
 Определитель транспонированной матрицы равен определителю исходной матрицы.
Определитель транспонированной матрицы равен определителю исходной матрицы.
45.Показать 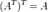
Дважды транспонированная матрица А равна исходной матрице А.

Следовательно 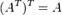 Ч.т.д.
Ч.т.д.
46.Показать (аА)Т=а(А)Т
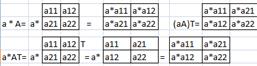
Т.к. ответы равны, следовательно утверждение (аА)Т=а(А)Т верно. Ч.т.д.
47.Показать (А+В)Т=(А)Т+(В)Т

Т.к. ответы равны, следовательно утверждение (А+В)Т=(А)Т+(В)Т верно. Ч.т.д.
48.Показать (А*В)Т=(В)Т*(А)Т


Т.к. ответы равны, следовательно утверждение (А*В)Т=(В)Т*(А)Т верно. Ч.т.д.
49. Сумма диагональных элементов: след (A*B)=след(B*A)

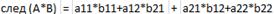

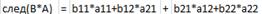
Т.к. 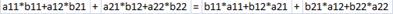 , следовательно след (A*B)=след(B*A). Ч.т.д.
, следовательно след (A*B)=след(B*A). Ч.т.д.
Дата добавления: 2018-08-06; просмотров: 1560; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
