Определение линейной комбинации множества векторов
Линейной комбинацией векторов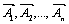 
, называется выражение вида: 
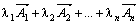, где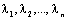 
– действительные числа, называемые коэффициентами линейной комбинации.
Определение линейной независимости векторов
Система векторов А1,А2,…Аn называется линейно независимой, если линейная комбинация этих векторов λ1*A1+λ2*A2+...+λn*An равна нулевому вектору только при нулевом наборе чисел λ1, λ2,...,λn, то есть система уравнений: A1x1+A2x2+...+Anxn =Θ имеет единственное нулевое решение.
Определение линейной зависимости векторов
Два вектора плоскости линейно зависимы тогда и только тогда, когда они коллинеарны.
Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых
Теорема о линейной зависимости векторов
Теорема о представлении строки в виде линейной комбинации независимых строк
Каждая строка матрицы А может быть представлена в виде линейной комбинации независимых строк матрицы А.
Пусть матрица А имеет ранг r ,тогда существует минор порядка r отличный от 0,добавим к этому минору i-ую строку и j-ый столбец
| а11 | а12 | … | а1r | a1j |
| a21 | a22 | … | a2r | a2j |
| … | … | … | … | … |
| a41 | a42 | … | a4r | a4j |
| ai1 | ai2 | … | air | aij |
Мr=
Mr+1=0; т.к. ранг A=r (как минор более высоеого порядка ,чем r).Этот минор можно разложить по последнему столбцу.
|
|
|
[а1jA1j + a2j A2j +…+ arj Arj + aij (-1)i+j *Mr]=0
Разделим все на Mr и введем Aij /( (-1)i+j Mr)=λi
aij = λ1 a1j +λ2 a2j +…+ λ4 a4j, где j=r+1 это равенство справедливо и для j=1m
81. Теорема о представлении cтолбца в виде линейной комбинации независимыхcтолбцов
Теорема о связи ранга матрицы с числом независимых строк/cтолбцов
Ранг матрицы А равен числу её независимых строк/столбцов.Пусть матрица А(m*n) имеет ранг r
| а11 | а12 | … | а1r |
| a21 | a22 | … | a2r |
| … | … | … | … |
| а21 | а22 | … | а2r |
Мr=
Существует минор порядка r = 0; {e1…..еr} –линейно-независимы
Пусть имеется противоположное : er = λ1 e1 +λ2 e2 +…+ λr-1 er-1
Проведем эле-ые преобр. не изменяющие определитель этого минора ( Mr )
er - λ1 e1
er - λ1 e1 - λ2 e2
er - λ1 e1 - λ2 e2 – λ3 e3 -…- λr-1 er-1
Итак,мы получим последнюю строку состоящую из 0,но тогда Mr = 0,наше предположение неверно!
Определители
Свойства определителей. № 01.(Транспонирование)
Определитель транспонированной матрицы равен определителю исходной матрицы: 
.
Доказательство. Согласно определению,
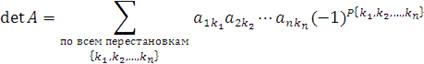
При транспонировании матрицы A происходит лишь перегруппировка слагаемых в этой сумме.
|
|
|
Свойства определителей. № 02. (Перестановка строк или столбцов).
Если в определителе переставить местами любые две строки или два столбца, то определитель изменяет свой знак на противоположный.
Доказательство. По Теореме 1, любая транспозиция изменяет четность перестановки. Следовательно, при перестановке двух строк (столбцов) каждое слагаемое суммы изменяет свой знак на противоположный.
Дата добавления: 2018-08-06; просмотров: 1458; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!