Условие возможности умножения матриц

Стр 1 из 6Следующая ⇒

Оглавление

Матрицы.. 4

1. Определение матрицы.. 4

2. Прямоугольная Матрица. 4

3. Матрица-строка. 4

4. Матрицей-столбец. 4

5. Главная диагональ матрицы. 4

6. Порядок матрицы. 4

7. Квадратная матрица. 4

8. Верхнетреугольная матрица. 4

9. Нижнетреугольная матрица. 4

10. Диагональная матрица. 5

11. Единичная матрица. 5

12. Нулевая матрица. 5

13. Симметричная матрица. 5

14. Кососимметричная матрица. 5

15. Ортонормированныя матрица. 5

16. Блочная матрица. 5

17. Расширенная Матрица. 5

18. Равные матрицы.. 5

19. Умножение числа на матрицу. 6

20. Сложение матриц. 6

21. Вычитание матриц. 6

22. Умножение матрицы на матрицу. 6

23. Условие возможности умножения матриц. 6

24. Антиперестановочность произведения матриц. 6

25,26Умножение матрицы на матрицу слева. Умножение матрицы на матрицу справа. 6

27. Условие перестановочности умножения матриц. 6

43. Возведение матрицы в степень. 10

44. Транспонированная матрица. 11

45.Показать 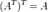........... 12

46.Показать (аА)Т=а(А)Т. 12

47.Показать (А+В)Т=(А)Т+(В)Т. 12

48.Показать (А*В)Т=(В)Т*(А)Т. 12

49. Сумма диагональных элементов: след (A*B)=след(B*A) 12

50.Элементарное преобразование матрицы № 1. 13

51. Элементарное преобразование матрицы № 2. 13

52. Элементарное преобразование матрицы № 3. 13

53. Элементарное преобразование матрицы № 4. 13

54. Элементарное преобразование матрицы № 5. 13

55. Элементарное преобразование матрицы № 6. 13

56. Теорема об умножении матрицы на матрицы элементарных преобразований. 14

57. Определение обратной матрицы.. 14

58. Невырожденная матрица. 14

59. Вырожденная матрица. 14

60. Теорема о существовании обратной матрицы.. 14

61. Показать (A^-1)^-1=(A) 14

62. Показать (A^-1)*A=E.. 14

63. Показать (A^T)^-1=(A^-1)^T. 15

64. Показать (A^-1)^T=(A^-1) для A^T=A.. 15

69. Вычисление обратной матрицы методом Гаусса-Жордана. 17

70. Вычисление обратной матрицы с помощью присоединенной матрицы(метод Крамера) 19

71. Определение минора к-го порядка. 21

72. Определение ранга матрицы через наивысший порядок минора. 21

73. Теорема о ранге матрицы при элементарных преобразованиях. 21

74. Эквивалентные матрицы. 21

75.Канонический вид матрицы. 22

76. Определение линейной комбинации множества векторов. 22

77. Определение линейной независимости векторов. 22

78. Определение линейной зависимости векторов. 22

79. Теорема о линейной зависимости векторов. 22

80. Теорема о представлении строки в виде линейной комбинации независимых строк. 22

81. Теорема о представлении cтолбца в виде линейной комбинации независимых. 23

82. Теорема о связи ранга матрицы с числом независимых строк/cтолбцов. 23

Определители. 23

1. Свойства определителей. № 01.(Транспонирование) 23

2.Свойства определителей. № 02. (Перестановка строк или столбцов). 24

3.Свойства определителей.. № 03.(Два одинаковых столбца или строки) 24

21. Общее число произведений в разложении определителя. 24

32. Определитель 2-го порядка как решение СЛАУ 2-го порядка. 26

33. Формула разложения определителя 3-го порядка. 26

34. Определитель 3-го порядка как решение СЛАУ 3-го порядка. 26

35. Метод звездочки разложения определителя 3-го порядка. 26

36. Метод параллельных прямых разложения определителя 3-го порядка. 27

Матрицы

Определение матрицы

Матрицей размера n×m называется прямоугольная таблица, состоящая из n строк и m столбцов, заполненная числами

Прямоугольная Матрица

Если m не равно n, то матрица будет называться прямоугольной

Матрица-строка

Матрица размером 1×n, т.е. состоящая из одной строки, называется матрицей-строкой.

Матрицей-столбец

Матрица размером m×1, т.е. состоящая из одного столбца, называется матрицей-столбцом

Главная диагональ матрицы.

Элементы расположенные на местах a₁₁, a₂₂ ,..., a_nn образуют главную диагональ матрицы.

Порядок матрицы.

Порядок матрицы - это другое название размерности матрицы, которое применяется для квадратных матриц. Говорят, что квадратная матрица с m строками и n столбцами имеет порядок m=n. (ну, к примеру: матрица 2-ого порядка означает 2 строки и 2 столбца в ней)

Квадратная матрица

Матрица A порядка m×n называется квадратной матрицей, если количество строк и столбцов совпадают: m=n. Число m=n называется порядком квадратной матрицы

Верхнетреугольная матрица

Квадратная матрица порядка n×n называется верхней треугольной матрицей, если равны нулю все элементы матрицы, расположенные под главной диагональю, т.е. a_ij=0, при всех i>j

Нижнетреугольная матрица

Квадратная матрица порядка n×n называется нижней треугольной матрицей, если равны нулю все элементы матрицы, расположенные над главной диагональю, т.е. a_ij=0, при всех i<j.

Диагональная матрица

Квадратная матрица называется диагональной, если элементы, расположенные вне главной диагонали равны нулю.

Единичная матрица

Квадратную матрицу n-го порядка, у которой на главной диагонали стоят единицы, а все остальные элементы равны нулю, называется единичной матрицей

Нулевая матрица

Если все элементы матрицы равны нулю, то матрица называется нулевой матрицей

Симметричная матрица

Матрица, удовлетворяющая условию A=A^T называется симметричной матрицей, т.е элементы в ней симметричны относительно гл. диагонали.

Кососимметричная матрица

Кососимметрической называется квадратная матрица, которая отличается от своей транспонированной матрицы множителем −1: A^T=−A. (то же что и симметричная, только с -1)

Ортонормированныя матрица

Ортонормированная матрица – матрица, столбцы и строки которой образуют системы ортонормированных векторов. Или проще говоря Ортогона́льная ма́трица — квадратная матрица A с вещественными элементами, результат умножения которой на транспонированную матрицу A^T равен единичной матрице, т.е она удовлетворяет условию 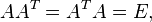или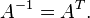

Блочная матрица

Блочная (клеточная) матрица — представление матрицы, при котором она рассекается вертикальными и горизонтальными линиями на прямоугольные части — блоки (клетки)

Расширенная Матрица

Расширенная матрица – это матрица системы линейных уравнений, к которой добавлен справа столбец правых частей системы – свободных членов.

Равные матрицы

Две матрицы называются равными, если они имеют одинаковые размеры и равные соответственные элементы:

A = {a_{i j}}_mn, B = {b_{i j}}_mn, A = B, если m = n, a_{i j} = b_{i j} , i = 1, 2, ..., m, j = 1, 2, ..., n.

Умножение числа на матрицу

Произведением матрицы 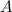наненулевое число 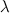называется матрица 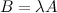того же порядка, полученная из исходной умножением на заданное число всех ее элементов:

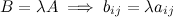
Сложение матриц

Суммой матриц 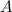и 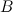одного размера называется матрица 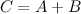такого же размера, получаемая из исходных путем сложения соответствующих элементов:

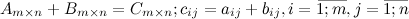
Вычитание матриц

Разностью матриц 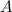и 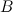одного и того же размера называется матрица 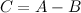такого же размера, получаемая из исходных путем прибавления к матрице 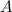матрицы 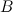, умноженной на (-1).

Умножение матрицы на матрицу

Произведением матрицы 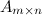на матрицу 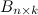называется матрица 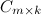такая, что элемент матрицы 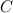, стоящий в 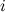-ой строке и 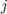-ом столбце, т.е. элемент 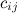, равен сумме произведений элементов 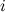-ой строки матрицы 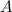на соответствующие элементы 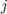-ого столбца матрицы .

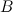Условие возможности умножения матриц

Умножать матрицы можно тогда и только тогда, когда количество столбцов первой матрицы равно количеству строк второй матрицы.

Дата добавления: 2018-08-06; просмотров: 1224; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 5 6 Следующая ⇒

Мы поможем в написании ваших работ!