Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.

y’’+ p₁*y’+ p₂*y= 0

y = e^kx; y’ = ke^kx; y’’ = k²e^kx.

e^kx(k²+p₁k+p₂) = 0

k²+p₁k+p₂= 0 – характеристическое уравнение второго порядка

Фундаментальная система решений и общее решение в случае различных действительных корней характеристического уравнения (формулировка, доказательство).

k_1,2∈R; k₁≠ k₂→y₁(x) = e^k1x; y₂(x) = e^k2x;

W(x) =	ek1x	ek2x	=	ek1x*ek2x	1	1	= e(k1+k2)x(k2 – k1) ≠ 0
	k1* ek1x	k2* ek2x			k1	k2

 

{e^k1x;e^k2x} - ФСР

Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.Фундаментальная система решений и общее решение в случае кратных действительных корней характеристического уравнения (формулировка, доказательство).

k_1,2∈R; k₁ = k₂→y₁(x) = e^k1x; y₂(x) = x*e^k1x;

W(x) =	ek1x	xek1x	=	ek1x*ek1x	1	x	= e2k1x(1+k1x– xk1) = e2k1x≠ 0
	k1* ek1x	ek1x + k1* xek1x			k1	1+k1x

{e^k1x;x*e^k1x} – ФСР

21. Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.Фундаментальная система решений и общее решение в случае комплексных корней характеристического уравнения (формулировка, доказательство), пример.

k_1,2∈C , k_1,2 = α+βi → y₁(x) =  ; y₂(x) =

W(x) =			=

 

=			=

= (  -  =
{ ; } – ФСР

 

Линейное неоднородное дифференциальное уравнение 2-го порядка. Метод вариации произвольных постоянных.

y’’+ p₁*y’+ p₂*y= q(x)

y_оо= С₁y₁(x) + С₂y₂(x)

y_он = С₁(x) y₁(x) + С₂(x) y₂(x)

Доказательство:

y_он = С₁(x) y₁(x) + С₂(x) y₂(x)

y_он’= С₁’(x) y₁(x) + С₁(x) y₁’(x) + С₂‘(x) y₂(x) + С₂(x) y₂’(x)

т.к. С₁’(x) y₁(x)+ С₂‘(x) y₂(x) = 0

то y_он’ = С₁(x) y₁’(x) + С₂(x) y₂’(x)

y_он’’= С₁’(x) y₁’(x) + С₁(x) y₁’’(x) + С₂‘(x) y₂’(x) + С₂(x) y₂’’(x)

Теперь вместо y, y’ иy’’ подставляем

С₁’(x) y₁’(x) + С₁(x) y₁’’(x) + С₂ ‘(x) y₂’(x) + С₂ (x) y₂’’(x) + p₁*(С₁ (x) y₁’(x) + С₂ (x) y₂’(x))+ p₂*(С₁ (x) y₁(x) + С₂ (x) y₂(x))

Группируем

С₁(x) (y₁’’(x) + p₁* y₁’(x) + p₂*y₁(x)) + С₂ (x) (y₂’’(x) + p₁* y₂’(x) + p₂*y₂(x)) + С₁’(x) y₁’(x) + С₂ ‘(x) y₂’(x) = q(x)

т.к. y₁’’(x) + p₁* y₁’(x) + p₂*y₁(x) = 0

  y₂’’(x) + p₁* y₂’(x) + p₂*y₂(x) = 0

С₁’(x) y₁’(x) + С₂ ‘(x) y₂’(x) = q(x)

то С₁(x)*0 + С₂ (x)*0 + q(x) = q(x)

Метод Крамера:

;

где

0≠∆ = W(x0) =	y1(x)	y2(x)
	y1’(x)	y2’(x)

 

∆1 =	0	y2(x)
		y2’(x)

∆2 =	y1(x)	0
	y1’(x)

 

ДУ 1-го порядка с разделяющимися переменными: метод решения.

 – ДУ с разделяющимися переменными

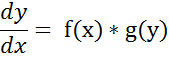
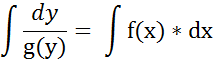
Однородное ДУ 1-го порядка: метод решения.

 - однородное ДУ 1-го порядка

Линейные дифференциальные уравнения 1-го порядка: метод решения.

 – ЛДУ 1-го порядка

Метод Бернулли:

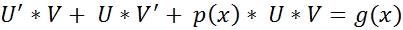
Решаем первое уравнение:

Подставляем полученное равенство во второе уравнение:

 =

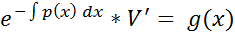
 + C

Ответ: y=U*V→y=

26. Метод понижения порядка для решения уравнения вида f (x, y’, y’’) = 0

Суть метода состоит в том, что с помощью замены переменной данное ДУ сводится к уравнению, порядок которого ниже.

f (x, y’, y’’) = 0 нет y→ замена

y’ = p(x)

y’’ = p’ =

---

Дата добавления: 2018-08-06; просмотров: 512; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!