Частное решение ДУ n-го порядка.

Частным решением ДУ n-го порядка называется решение ДУ, полученное из общего решения при конкретных значениях постоянных C₁, C₂, …, C_n

13. Линейные однородные дифференциальные уравнения (ЛОДУ) 2-го порядка.

ЛОДУ 2-го порядка называются уравнения вида:

y’’ + p₁(x)*y’ + p₀(x)*y = 0

ЛОДУ всегда имеет тождественно равное нулю решение, которое называется нулевым или тривиальным.

Простейшие свойства решений (доказательство одного из них)

1) Если y₁(x) и y₂(x) – решения ЛОДУ, тоy = y₁(x) + y₂(x) – тоже решение ЛОДУ

2) Если y(x) – решение ЛОДУ, то для любого λ*y(x) –тоже решение ЛОДУ

Доказательство 1-го свойства:

y’’ + p₁(x)*y’ + p₀(x)*y = 0

Дано: y₁(x) и y₂(x) – решения ЛОДУ

Доказать: y = y₁(x) + y₂(x) – тоже решение ЛОДУ

Доказательство:

y = y₁(x) + y₂(x)

y’ = y₁’(x) + y₂’(x)

y’’ = y₁’’(x) + y₂’’(x)

Подставим в исходное уравнение:

y₁’’(x) + y₂’’(x) + p₁(x)*(y₁’(x) + y₂’(x)) + p₀(x)*(y₁(x) + y₂(x)) = 0

y₁’’(x) + p₁(x)*y₁’(x) + p₀(x)*y₁(x) + y₂’’(x) + p₁(x)* y₂’(x) + p₀(x)* y₂(x) = 0

т.к. y₁(x) и y₂(x) – решения ЛОДУ, то

y₁’’(x) + p₁(x)*y₁’(x) + p₀(x)*y₁(x) = 0

и

y₂’’(x) + p₁(x)* y₂’(x) + p₀(x)* y₂(x) = 0

→y = y₁(x) + y₂(x) – тоже решение ЛОДУ

14. Линейная зависимость двух функций.

Система функций y₁(x) и y₂(x) называется линейно зависимой, если найдется хотя бы один коэффициент λ_i ≠ 0, при котором линейная комбинация этих функций тождественно равна нулю.

0 *y₁(x) + λ₂ * y₂(x) = 0

λ₁* y₁(x) + 0* y₂(x) = 0

Линейная независимость системы двух функций.

Система функций y₁(x) и y₂(x) называется линейно независимой, если линейная комбинация этих функций тождественно равна нулю только тогда, когда все коэффициенты λ₁и λ₂равны нулю.

0 * y₁(x) + 0* y₂(x) = 0

Следствие: Если 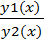≠ const , y₁(x) и y₂(x) – линейно независимы; а если 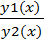= const, то y₁(x) и y₂(x) – линейно зависимы.

Условие линейной зависимости двух функций

Система двух функций y₁(x) и y₂(x) является линейно зависимой в интервале (a, b), если определитель Вронского равен нулю во всех точках этого интервала.

Условие линейной независимости двух функций

Система двух функций y₁(x) и y₂(x) является линейно независимой в интервале (a, b), когда определитель Вронского отличен от нуля хотя бы в одной точке этого интервала.

Определитель Вронского

Определителем Вронского системы функций y₁(x) и y₂(x) называется определитель вида:

W(x) =	y1(x)	y2(x)
	y1’(x)	y2’(x)

 

Свойства определителя Вронского для линейной зависимости системы двух функций (доказательство)

Дано: {y₁(x);y₂(x)} – линейно зависимая на (a, b)

Доказать: W(x) = 0;∀x∈ (a, b)

Доказательство: {y₁(x);y₂(x)} – линейно зависимая на (a, b)

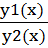= const → y₁(x) = С * y₂(x)

W(x) =	y1(x)	y2(x)	=	Сy2(x)	y2(x)	= Сy2(x)* y2’(x) - y2(x)*Сy2’(x) = 0
	y1’(x)	y2’(x)		Сy2’(x)	y2’(x)

 

15. Определение фундаментальной системы решений линейного однородного дифференциального уравнения (ЛОДУ) n-го порядка

Система функций {y₁(x); y₂(x); …; y_n(x)}, состоящая из n линейно независимых решений ЛОДУ n-го порядка, называется фундаментальной системой решений (ФСР) этого уравнения

Определение фундаментальной системы решений ЛОДУ 2-го порядка

Для ЛОДУ 2-го порядка ФСР состоит из 2 линейно независимых решений этого уравнения.

---

Дата добавления: 2018-08-06; просмотров: 623; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!