Формула Ньютона-Лейбница (вывод)
Первообразная функция. Функция F(x) называется первообразной от функции f(x)на отрезке [a, b], если во всех точках этого отрезка выполняется равенство F’(x)=f(x).
Теорема о разности двух первообразных (с доказательством)
Если F1(x) иF2(x) – две первообразные от функции f(x) на отрезке [a, b], то разность между ними равна постоянному числу.
Дано:F1(x) иF2(x) – первообразные от функции f(x)
Доказать:C = F2(x)- F1(x)
Доказательство:
F1’(x)=f(x)
F2’(x)=f(x)
R(x)= F2(x)- F1(x)
R’(x)= [ F2(x)- F1(x)]’=F2’(x)-F1’(x)=f(x)-f(x)=0
R’(x)=0
x0-фиксированная точка
x-произвольная любая точка
применяем теорему Лагранжа(x0 <ξ<x)
R(x)-R(x0)=R’(ξ)(x-x0)
R’(ξ)=0
R(x)-R(x0) = 0
R(x)=R(x0)
R(x)= R(x0) = const =C
R(x0) = C => R(x)= C
C = F2(x)- F1(x)
Определение неопределенного интеграла:
Неопределенным интегралом для f(x) называется все семейство первообразных.
∫f(x)dx=F(x)+Cf(x)-подынтегральная функция
f(x)dx –подынтегральное выражение
Свойства неопределённых интегралов с доказательством одного из них
1) ∫[f1(x)±f2(x)]dx = ∫f1(x)dx± ∫f2(x)dx
2) ∫K*f(x)dx = K∫f(x)dx
3) свойство инвариантности неопределенного интеграла
∫f(x)dx=F(x)+C, то С=t(x)
∫f(x)dx=F(t)+C - неизменность формы записи.
Доказательство первого свойства:
[f1(x) ± f2(x)]
[f1(x) dx ± f2(x) dx]’ = [f1(x) dx]’ ± [f2(x) dx]’= f1(x)±f2(x)
Справа – семейство первообразных для f1(x) ±f2(x)
2. Задача о площади криволинейной трапеции, приводящая к понятию определенного интеграла по отрезку.
Пусть на отрезке [a,b] задана непрерывная функция f(x)>0. Фигура, ограниченная графиком прямыми x=a, x=b и отрезком [a,b] оси ОХ называется криволинейной трапецией.
|
|
|
Разделим [a,b] точками a=x0 <x1<x2< … <xn-1<xn =bи пусть λ =max. Прямые разбивают трапецию на n узких полос. Так как функция f(x) непрерывна, то она мало меняется при xn-1≤x≤xnи без большой погрешности ее можно считать на [xn-1; xn] постоянной и равной f(ξn-1), где ξn-1 – произвольно взятая точка промежутка[xn-1; xn]
Sступ. фигуры = 
f(ξk)(xk - xk-1)
Sступ. фигуры= Sступ. трапеции
Sтрапеции = 
f(ξk)(xk - xk-1)
Определение определённого интеграла по отрезку.
Определенным интегралом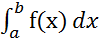 
по отрезку [a,b] называется предел интегральной суммы f(ξk)(xk - xk-1) при стремлении к нулю наибольшего из участков разбиения, если этот предел не зависит ни от способа разбиения отрезка, ни от выбора точек.
f(ξk)( xk - xk-1)
3. Вычисление определенного интеграла по отрезку.
Пусть на отрезке [a,b] задана непрерывная функция f(x)
1) Разобьем [a,b] на части точками a=x0 <x1<x2< … <xn-1<xn =b ; причем наибольшая из разностей xk - xk-1обозначим 
.
2) В каждом частичном промежутке [xk - xk-1] выберем по точке ξkи вычислим f(ξk)
3) Умножим f(ξk) на длину (xk - xk-1)соответствующего промежутка [xk - xk-1].
4) Сложим все найденные произведения.
|
|
|
S= f(ξk)( xk - xk-1)сумму будем называтьинтегральной суммой
Будем изменять произведенное дробление [a,b], так чтобы величина стремилась к нулю. Если при этом существует конечный предел,
J= f(ξk)(xk - xk-1)
не зависящий от выбора точек ξkи способа разбиения, то этот предел называется определенным интегралом от функции f(x) по [a,b] и обозначается
Формула Ньютона-Лейбница (вывод)
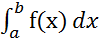= F(x) 
=F(b) – F(a)
Для вычисления определенного интеграла сначала следует вычислить неопределенный интеграл, а затем подставить пределы интегрирования (сначала верхний, а потом нижний)
= F(x) =F(b) – F(a)
Разделим [a,b] точками a=x0 <x1<x2< … <xn-1<xn =b
F(b) – F(a) = F(xn) – F(xn-1)) + (F(xn-1)- F(xn-2)) + (F(x1)- F(x0)) = (F(xk)-F(xk-1))
Применим к каждой разности в скобках теорему Лагранжа:
F(xk)-F(xk-1) = F’(ξk)*(xk-xk-1), k=1,2,…,n ; ξk∈(xk-xk-1)
F(b) – F(a) = F’(ξk)*(xk-xk-1) = f(ξk)*Δxk
F(b) – F(a)= f(ξk)*Δxk
Т.к. f(x) непрерывна на [a,b], то она интегрируема на [a,b]
F(b) – F(a)= f(ξk)*Δxk
=maxΔxk ; F(b) – F(a) =
4. Определение определённого интеграла по отрезку.
Определенным интегралом 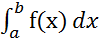по отрезку [a,b] называется предел интегральной суммы f(ξk)( xk - xk-1) при стремлении к нулю наибольшего из участков разбиения, если этот предел не зависит ни от способа разбиения отрезка, ни от выбора точек.
|
|
|
f(ξk)( xk - xk-1)
Дата добавления: 2018-08-06; просмотров: 3138; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!