Вопрос 44. Теорема о существовании и непрерывности обратной функции для строго монотонной непрерывной функции. Примеры.
Теорема. Пусть f:X®R строго монотонная и непрерывная на X=[a,b] тогда обратная функция f-1 определена, строго монотонная и непрерывная на отрезке с концами в точках f(a) и f(b) ([f(a),f(b)]).
Доказательство. Существование обратной функции следует из строгой монотонности. Кроме того, обратная функция также будет монотонной с областью значений [a,b]. Из критерия непрерывности монотонной функции следует ее непрерывность ( монот. функция будет непрерывна на [a,b] тогда и только тогда когда множество f([a,b]) ее значений само является отрезком с концами f(a) и f(b)).
| y |
| x |
| y |
| x |
| a |
| b |
| f(b) |
| f(a) |
| f(a) |
| f(b) |
| b |
| a |
Вопрос 45. Равномерная непрерывность. Теорема Кантора.
Функция f:Е®R называется равномерно непрерывной на множестве Еесли для "e>0найдется $d>0, такое что для "x1,x2ÎE, таких что |x1-x2|<d, выполнено |f(x1)-f(x2)|<e.
Теорема (Кантор). Функция непрерывная на отрезке [a,b] равномерно непрерывна на этом отрезке.
Доказательство. Предположим противное $e0>0 такое что для "d>0, найдется x',x″Î[a,b], |x'-x″|<d, но при этом |f(x')-f(x″)|≥e0. Возьмем {dn}, dn®0 при n®¥, тогда найдутся значения x'n, x″nÎ[a,b], такие что |x'n-x″n|<dn, тогда как |f(x'n)-f(x″n)|≥e0, по теореме (Больцано-Вейерштраса) из ограниченной последовательности {x'n} можно извлечь сходящуюся подпоследовательность {x'nk}, x'nk®0, при k®¥ т.к. |x'nk-x″nk|<dnk, то x″nk также сходится к x0, k®¥. Поэтому ввиду непрерывности функции в точке х0, переход к пределу в неравенство |f(x'nk)-f(x″nk)|≥e0 даст 0=|f(x0)-f(x0)|≥e0 (e0>0), что противоречит. (в этом доказательстве x0Îdn, limdn=x0)
|
|
|
Вопрос 46. Определение показательной функции на основе теории предела. Корректность определения.
Определение показ. функции. Пусть a>0,"xÎR,rn®x, n®¥, rnÎQ,положим ax:=limn®¥arn (1)
Утверждение: определение корректно, т.е. предел (1) существует и не зависит от выбора {rn}.
Доказательство. Пусть rn®x, покажем что {arn} является фундаментальной. Имеем |arn-arm|=arm|arn-rm-1| (2). Последовательность {rn} сходится и следовательно ограниченна. При этом очевидно $AÎQ, при этом всем номерам nÎN, выполняется –А<rn<A, отсюда при а≥1 имеем a-A≤arn≤aA. Поэтому при "а>0 $B такое что arn≤В (3) для "nÎN (B=aA, при a>1; B=a-A, при a<1).
По лемме 2 "e>0 $d=d(e)>0, такое что для "rÎQ, |r|<d выполняется |ar-1|< 
(4). Из сходимости {rn} что для найденного d $nd, такое что для всех номеров n>nd; m>nd, |rn-rm|<d, поэтому в силу (2)(3)(4) |arn-arm|<B 
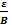=e. В силу критерия Коши последовательность {arn}сходится.
Пусть теперь {r¢n}®x, r¢nÎQ, покажем что limn®∞arn = limn®∞ar¢n,составим новую последовательность {r²n}={r1, r¢1, r2, r¢2…rn, r¢n} очевидно r²n®x, поэтому в силу доказанного $ lim ar²n , отсюда для ее последовательности имеем limn®¥arn= limn®¥ar¢n= limn®¥ar²n
|
|
|
Вопрос 47. Свойства показательной функции (пять свойств).
1) a>1, ax (строго возрастает) на R; a<1, ax¯¯ на R.
2) axay=ax+y, x,yÎR.
3) (ax)y=axy.
4) Функция ax непрерывна на R.
5) Множеством значений ax является множество R+=(0;+∞).
Доказательства:
1) Пусть для определенности a>1, x<y. $ такие иррац. числа r¢, r², такие что x<r¢<r²<y, выберем какие либо посл-ти иррациональных чисел {r¢n}, {r²n}, r¢n<r¢<r²<r²n для " номеров nÎN и что r¢n®x, r²n®y при n®∞, тогда ar¢n< ar¢<ar²< ar²n, перейдя к пределу при n®∞ получим ax< ar¢<ar²< ay. В случай a<1 рассм. аналогично.
2) Пусть r¢n®x, r²n®y, r¢n,r²nÎQ, значит r¢n+r²n®x+y, тогда в силу опред. показ. ф-ции ax+y=limn®∞ar¢n+r²n= limn®∞ar¢n×limn®∞ar²n=axay. Отметим, что из того что axa-x=a0=1 следует равенство a-x=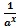 
, отсюда же с учетом монот. ax (либо ax>1, либо a-x>1), Þ ax>0, для "xÎR.
3) Поверим в начале, что свойство 3 имеет место при " иррац. y. Если y=mÎN, то (ax)m=ax×…×ax=ax+…+x=axm; если y=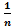 
, nÎN то (ax)1/n=ax/n т.к. по доказанному (ax/n)n=ax; если y= 
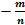, m,nÎN, то (ax)-m/n= 
= 
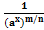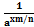= a-xm/n. Пусть задана уÎR, рассм. произведение посл. rn рац. чисел сходящ. к у (rn®y) тогда (ax)rn=axrn, переходя в этом равенстве к пределу пользуясь определением показ. ф-ции и ее непрерывн. получим (ax)y=axy.
|
|
|
4) Для "e>0 $d>0, что для "hÎR таких что |h|<d, вып. нер-во |an-1|<e. Пусть х фиксир., y=ax, ∆y=ax+∆x-ax=ax(a∆x-1). Согласно сказанному для "e>0 $d>0 что для "∆х, таких что |∆х|<d, выполн. нер-во |a∆x-1|<e/ax отсюда при |∆х|<d имеем |∆y|=ax|a∆x-1|<e, что обознач. непрерывн. ф-ции ах в точке х.
5) При a>1 в силу непрер. и возр. ф-ции y=ax достаточно показать что limх®+¥aх=-∞, limх®-¥aх=0,поскольку пределы (кон. или бескон.) существуют, для этого дост. заметить что дляnÎN, limх®¥an=+∞, limх®¥a-n =0, при a<1, b=1/a>1, limх®+¥aх=limх®+¥1/x=0, limх®-¥aх=limх®-¥1/b=+∞.
Дата добавления: 2018-08-06; просмотров: 1055; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!