Вопрос 31. Критерий коши существования предела функции.

       Теорема (Коши). Для того чтобы f имела в точке аÎ  конечный предел необходимо и достаточно чтобы для "e>0 существовала $ (a)= (a,d) точки а, чтоб для любых "x′,x″Î (a) выполнялось бы неравенство |f(x′)-f(x″)|<e (1).

       Доказательство.

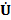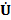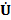Необходимо. Пусть предел lim_x®af(x)=AÎR, тогда для "e>0 существует $ (a) такая, что для "xÎ (a) выполняется неравенство |f(x)-A|<  , так что для "x′,x″Î (a) выполняется

|f(x′)-f(x″)|≤|f(x′)-A|+|f(x″)+A|< = e.                                                                      

Достаточно. Пусть e>0 и 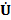(a) такая окрестность, что для "x′,x″Î 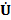(a) выполняется неравенство (1). Возьмем, какую либо последовательность {x_n}, x_n¹a, lim_n®¥x_n=a, в силу определения предела последовательности $n₀, что для "n>n₀, x_nÎ 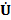(a) от суда и следует, что |f(x′)-f(x″)|<e.

Это означает, что последовательность {f(x_n)} удовлетворяет критерию сходимости Коши для последовательностей и следовательно имеет конечный предел, от сюда и из определения предела по Гейне следует что f имеет в точке а конечный предел.

 

Вопрос 32. Свойства пределов функций (локальная ограниченность, сохранение знака, переход к пределу в неравенствах; свойства, связанные с арифметическими действиями над функциями).

1) Локальная ограниченность.Если у функции заданной точки $ конечный предел, то в некоторой проколотой окрестности этой точки а ограниченна.

Доказательство.Пусть lim_x®af(x)=A, тогда для "e>0, в частности для e=1, $ 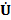(a,d)в точке а, такая что для "xÎ 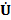(a,d)имеет местоf(x)ÎU(A,1)т.е.A-1<f(x)<A+1.

2) Сохранение знака.Если уfзаданной точкиа $конечный пределlim_x®af(x)=A¹0,то в некоторой окрестности 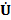(a), fимеет тот же знак что и указанный предел.

Доказательство. Пусть lim_x®af(x)=A, A>0тогда для"e>0,в частности дляe=А, $ 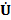(a,d)такая что для"xÎ 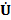(a,d)имеемf(x)Î 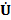(A,A)т.е.А-А<f(x)<A+A,так чтоf(x)>0.

3) Переход к пределу в неравенствах. Теорема. Если f(x), g(x) определены на ,x₀Î(a,b) и f(x)< g(x) на  и существуют пределы , А и B числа, то A<B.

Арифметические действия:

1) , , если $ .

2) , если существуют конечные пределы , .

3) , если существуют конечные пределы , .

4) $ Þ$

5) g(x)¹0, , $ Þ$

Следствие: , если существует конечный предел .

 

Вопрос 33. Теорема о сложной функции.

       Теорема. Пусть$ конечный или бесконечныйlim_x®af(x)=b, lim_y®bF(y) и пусть при этом в некоторойŮ(a) точкиа,f(x)¹0, тогда в некоторой Ů(a,d₀) определена сложная функцияF(f(x)) и$ lim_x®aF(f(x))=lim_y®bF(y).

       Доказательство. Пусть функция F(y) определена в некоторой Ů(b,e₀),поскольку lim_x®af(x)=b,то при некоторойd₀>0имеемf(Ů(a,d₀))ÌŮ(b,e₀) и Ů(a,d₀)Ì Ů(a).

Таким образом в окрестностиŮ(a,d₀)определена функцияF(f(x)).

Пусть теперь последовательностьx_nΠŮ(a,d₀), x_n®a.Положимy_n=f(x_n),очевидноy_nÎŮ(b,e₀)при этом согласно определению предела функции по Гейне, lim_n®¥y_n=b,из существования пределов lim_y®bF(y)=:A следует что $lim_n®¥F(y_n)= lim_n®¥F(f(x_n))=A, а это и означает что limF(f(x))=A.

 

 

---

Дата добавления: 2018-08-06; просмотров: 487; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!