Вопрос 18. Переход к пределу в неравенствах. Последовательности ограниченные и неограниченные.
Теорема 3 (о переходе к пределу в неравенстве). Если limn®¥xn=a, limn®¥yn=b, aÎ 
, bÎ и для"nÎN, xn≥yn тоÞ a≥b.
Доказательство: Если бы оказалось что a<b, то согласно Лемме 1, нашелся бы $n0 что для "n>n0 выполнялось бы неравенство xn<yn что против xn≥yn.
Числовая последовательность называется ограниченной сверху (снизу), если множество ее значений ограниченно сверху (снизу).
Иначе говоря последовательность {xn} называется ограниченной сверху (снизу),если существует такое число $сÎR, что для "nÎR выполняется неравенство xn≤c (xn≥c).
Последовательность ограниченная как сверху так и снизу называется ограниченной.
Последовательность не являющаяся ограниченной сверху (снизу), называется неограниченной.
Вопрос 19. Ограниченность сходящихся числовых последовательностей.
Теорема. Если числовая последовательность имеет конечный предел, то она ограничена.
Доказательство: Пусть limn®¥xn=a, тогда согласно определению предела, существует $n0, что для всех "n>n0, |xn-a|<1(1) (в определении предела взяли e=1). Обозначим через d наибольший из чисел d=max{1, |xn-a|…|xn0-a|} тогда в силу (1) для "n>N имеем a-d≤xn≤a+d
Вопрос 20. Бесконечно малые последовательности и их свойства.
Числовая последовательность, предел которой равен нулю, называется бесконечно малой.
Свойства б.м. последовательностей:
|
|
|
1) Любая конечная, линейная комбинация б.м. последовательностей является бесконечно малой.
Доказательство: Пусть {αn} и {βn} б.м. последовательности a λ и μÎR, "e>0, c>|λ|+|μ| тогда существует $n0, что для любого "n>n0 выполняется неравенство |αn|< 
, |βn|< 
, отсюда |λαn+μβn| ≤ |λ||αn|+|μ||βn| ≤ (|λ|+|μ|) 
, a это означает что λ{αn}+μ{βn} бесконечно малая последовательность.
2) Произведение бесконечно малых последовательностей на ограниченную последовательность является бесконечно малой.
Доказательство: Пусть limn®¥αn=0,а{xn}ограниченная последовательность т.е.с>0,что для всех"nÎNвыполняется|xn|≤c,возьмем"e≥0,тогда по определению предела существует $n0, что для всех "n>n0 выполняется неравенство |αn|≤ , при n>n0, |αn×xn|=|αn||xn|< c=e,а это и означает что {αn×xn} бесконечно малая последовательность.
Вопрос 21. Свойства пределов, связанные с арифметическими действиями над последовательностями (lim(xn+yn), lim(xnyn)).
2°. Конечная, линейная комбинация сходящихся последовательностей также является сходящейся последовательностью и ее предел равен такой же линейной комбинации предела данных последовательностей.
|
|
|
Доказательство: lim xn=a, lim yn=b, a и bÎR тогда в силу леммы 1, xn=a+αn, yn=b+βn, где {αn} {βn}- б.м. Пусть λ, μÎR, λxn+μyn=λa+μb+λαn+μβn, n=1,2… по свойству 1 §4 (любая конечная, линейная комбинация б.м. является б.м.), {λαn+μβn}- б.м. Поэтому в силу леммы 1, limn®¥(λxn+μyn)=λa+μb.
3°. Если последовательности {xn} и {yn} сходятся, то их произведения также сходятся и их пределы lim(xnyn)= lim xn×lim yn.
Доказательство: Пусть lim xn=a, lim yn=b, тогда xn=a+αn, yn=b+βn, где {αn}, {βn} – б.м. поэтому xnyn=(a+αn)(b+βn)=ab+(bαn+aβn+αnβn)=γm, где {γm} – б.м.(см. св.1,2 §4)(1.любая конечная, линейная комбинация б.м. является б.м.; 2.Произведение б.м. последовательностей на ограниченную последовательность является б.м.). Отсюда из леммы 1 получаем предел limn®¥xnyn=ab.
Вопрос 22. Предел частного lim(xn/yn).
Если последовательность {xn} и {yn} сходятся, yn¹0 для "nÎN и limn®¥yn¹0, то {xn/yn} сходится, причем limn®¥xn/yn= limn®¥xn/limn®¥yn.
Доказательство:пустьlim xn=a, lim yn=b,тогда xn=a+an, yn=b+βn, an и βn – б.м.
lim|yn|=|b|, 0< 
<|b|,согласно лемме 1, существует n0, для любого n>n0, |yn|> , 
(1).
- 
= 
- 
= 
(2).
Здесь последовательность 
ограничена: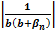 
= 
< 
(см. 1)
|
|
|
Поэтому последовательность 
является бесконечно малой как произведение ограниченной на бесконечно малую, отсюда из (2) следует требуемое.
Дата добавления: 2018-08-06; просмотров: 368; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!