Вопрос 34. Бесконечно малые и бесконечно большие функции и связь между ними.
Функция a(x)называется бесконечно малой(приx®a)еслиlimx®aa(x)=0.
Функция a(x)называется бесконечно большой(приx®a)еслиlimx®aa(x)=¥.
Теорема 2. Функцияa(x) неравная нулю в некоторой проколотой окрестностиŮ(a) является бесконечно малой (приx®a) тогда и только тогда когда1/a(x) является бесконечно большой(приx®a).
Вопрос 35. Теорема о существовании односторонних пределов у монотонной функции.
Теорема. Пусть f возрастает на конечном или бесконечном интервале (a,b), тогда в точке x=b, limx®b-0f(x)=sup(a,b)f(x), а в точке x=a, limx®a+0f(x)=inf(a,b)f(x).
Следствие. Если функция монотонна на (a,b) тогда x0Î(a,b) то в точке x0 существуют конечные, односторонние пределы: f(x0-0), f(x0+0).
Доказательство. Пусть β:=sup(a,b)f(x)Î  , зададим произвольную окрестность U(β) точки β и пусть β'-левый ее конец, β'<β. Тогда существует такая точка ξÎ(a,b), что f(ξ)>β'. Положим
, зададим произвольную окрестность U(β) точки β и пусть β'-левый ее конец, β'<β. Тогда существует такая точка ξÎ(a,b), что f(ξ)>β'. Положим  (b):=(ξ,b), тогда для "xÎ
(b):=(ξ,b), тогда для "xÎ  (b) в силу возрастания функции, β'<f(ξ)≤f(x)≤β т.е. f(x)ÎU(β).
(b) в силу возрастания функции, β'<f(ξ)≤f(x)≤β т.е. f(x)ÎU(β).
Итак для "U(β) существует такая проколотая левосторонняя  (а,b), что для "xÎ
(а,b), что для "xÎ  (а,b) имеем f(x)Î
(а,b) имеем f(x)Î  (b) это и означает что limx®b-0f(x)=sup(a,b)f(x).
(b) это и означает что limx®b-0f(x)=sup(a,b)f(x).
Аналогично для limx®а+0f(x)=inf(a,b)f(x).
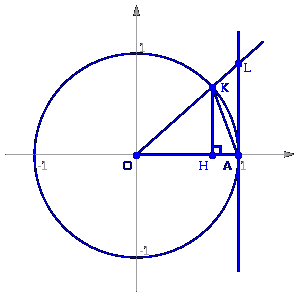 Вопрос 36. Предел limx®0
Вопрос 36. Предел limx®0  .
.
limx®0 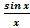 =1.
=1.
Доказательство.Рассмотрим односторонние пределы limx®0+  и limx®0-
и limx®0-  и докажем, что они равны 1.
и докажем, что они равны 1.
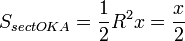 ПустьxÎ(0;
ПустьxÎ(0;  ).Отложим этот угол на единичной окружности (R=1). Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке (1;0). Точка H — проекция точки K на ось OX. Очевидно, что: SDOKA<SsectOKA<SDOAL (1).
).Отложим этот угол на единичной окружности (R=1). Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке (1;0). Точка H — проекция точки K на ось OX. Очевидно, что: SDOKA<SsectOKA<SDOAL (1).
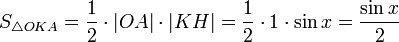
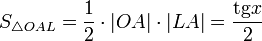
(из DOAL:| LA | = tgx); Подставляя в (1), получим: 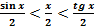
или sin(x)<x<tg(x). Разделив все части неравенства на sin x > 0, получим при условии х > 0:
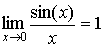
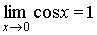
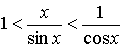 или
или 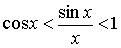 . Так как функция у = cos x непрерывна, то . Пользуясь теоремой о пределе промежуточной функции(о двух милиционерах), получим .
. Так как функция у = cos x непрерывна, то . Пользуясь теоремой о пределе промежуточной функции(о двух милиционерах), получим .
 Вопрос 37. Непрерывность функции в точке. Односторонняя непрерывность функции в точке. Примеры.
Вопрос 37. Непрерывность функции в точке. Односторонняя непрерывность функции в точке. Примеры.
Функция определенная в некоторой окрестности точки а, называется непрерывной в этой точке если limx®af(x)=f(a).
Пусть функция определена на полуинтервале (a,x0] ([x0,a)), функция называется непрерывной слева (справа) в точке х0 если limx®x-0f(x)=f(x0) (limx®x+0f(x)=f(x0)).
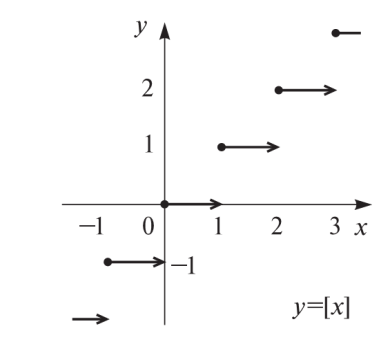
Пример. f(x)=[x] –наибольшее целое число, меньшее или равноех.
f(x)=[x]непрерывна справа во всех точкахх.
Вопрос 38. Точки разрыва первого и второго рода. Примеры.
Если f:(a,b)®R не является непрерывной в некоторой точке x0Î(a,b) и имеются конечные пределы справа и слева f(x0+0)=limx®x0+0f(x), f(x0-0)=limx®x0-0f(x), то эта точка называется точкой разрыва первого рода.
Если f:(a,b)®R не является непрерывной в некоторой точке x0Î(a,b)и имеется конечный предел либо справа f(x0+0)=limx®x0+0f(x), либо слева f(x0-0)=limx®x0-0f(x) или оба отсутствуют, то такая точка называется точкой разрыва второго рода.
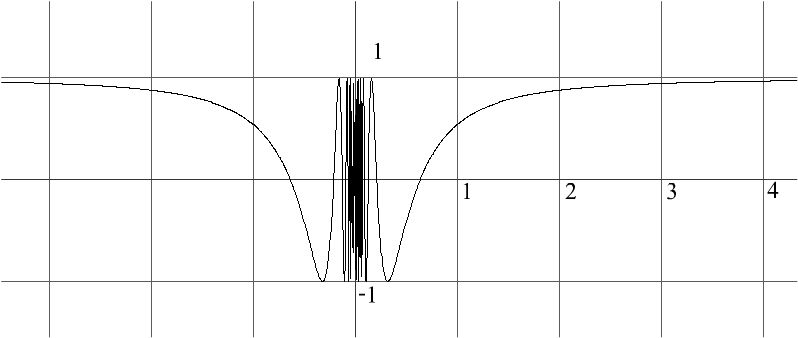 Пример. Пример 1. Функция
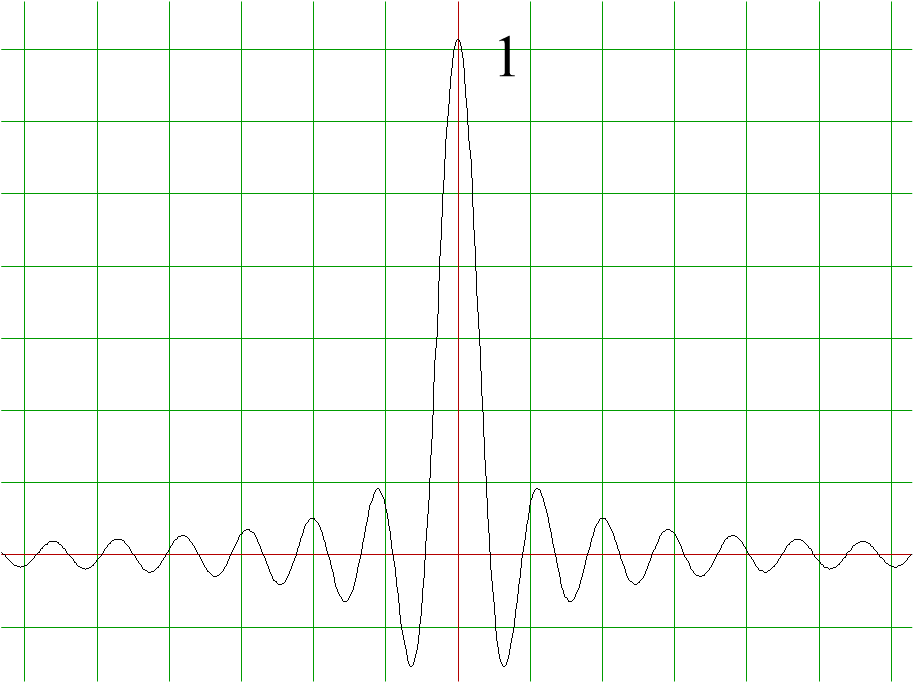
Пример. Пример 1. Функция 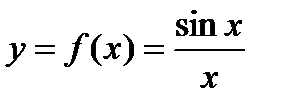 имеет устранимый разрыв первого рода в точке
имеет устранимый разрыв первого рода в точке 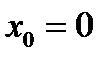 .
.
Пример 2. Функция 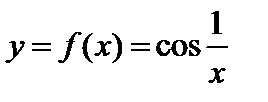 имеет разрыв второго рода в точке
имеет разрыв второго рода в точке 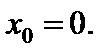
Вопрос 39. Локальные свойства функций, непрерывных в точке (теорема о локальной ограниченности, теорема о сохранении знака, теорема о непрерывности суммы, произведения, частного, теорема о непрерывности композиции двух непрерывных функций).
Теорема 1. f:(a,b)®R функция непрерывна в точке x0Î(a,b), тогда справедливы следующие утверждения:
1) f ограничена в некоторой окрестностиU(x0)точких0.
2)Еслиf(x0)¹0,то в некоторой окрестностиU(x0)точки х0все значения функции положительные или отрицательные т.е. sign f(x)=sign f(x0).
Доказательство случая 2. Непрерывность в точке х0, в частности обозначает, что f определена некоторой окрестности точких0.Пусть для определенности,f(x0)=d>0.Возьмемe=  >0.Тогда по определению непрерывности $d>0: |f(x)-f(x0)|<e=
>0.Тогда по определению непрерывности $d>0: |f(x)-f(x0)|<e= 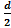 , "x:|x-x0|<d,откуда следует, чтоf(x)=f(x0)+(f(x)-f(x0))>d-
, "x:|x-x0|<d,откуда следует, чтоf(x)=f(x0)+(f(x)-f(x0))>d- 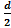 =
=  ,приxÎUd(x0).
,приxÎUd(x0).
Теорема 2. Если функцииf иg непрерывны в точкех0,то функциисf, f+g, fg, а также при условииg(x0)¹0, 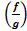 непрерывны в точке х0. Докажем лишь что f/g непрерывна в х0 (для остальных аналогично). g(x)¹0 при xÎU(x0) и частноеf/g определено наU(x0). Используя свойства пределов и непрерывность f и g: limx®x0(f/g)(x)= limx®x0f(x)/g(x)= limx®x0f(x)/ limx®x0g(x)=f(x0)/g(x0)=(f/g)(x0).
непрерывны в точке х0. Докажем лишь что f/g непрерывна в х0 (для остальных аналогично). g(x)¹0 при xÎU(x0) и частноеf/g определено наU(x0). Используя свойства пределов и непрерывность f и g: limx®x0(f/g)(x)= limx®x0f(x)/g(x)= limx®x0f(x)/ limx®x0g(x)=f(x0)/g(x0)=(f/g)(x0).
Теорема 3. Пусть функцияy=f(x) непрерывна в точкех0,а функцияF(y) непрерывна в точкеy0=f(x0), тогда композиция(Fof)(x):=F(f(x)) непрерывна в точкех0.
Это утверждение является следствием теоремы по пределу сложных функций, в силу которойlimx®x0F(f(x))=limy®y0F(y)=F(y0)=F(f(x0)),что равносильно суперпозиции в точке х0.
Дата добавления: 2018-08-06; просмотров: 262; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
