Построение семи-, восьми- и девятиугольников

По радиусу описанной окружности

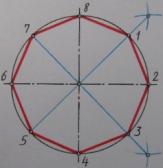
1.3.5 Построение правильного семиугольника по радиусу описанной окружности
1.3.6 Построение правильного восьмиугольника по радиусу описанной окружности
1.3.7 Построение правильного девятиугольника по радиусу описанной окружности
Построение n-угольников
1.3.8 Приближённый способ построения правильных многоугольников, например, правильного девятиугольника
1.3.9 Построение многоугольника, равного данному		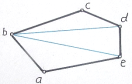- Провести в данном пятиугольнике аbсdедиагонали bd и bе, которые разделят пятиугольник на три треугольника. - Построить треугольник АВЕ, равный треугольнику аbе: отложить на произвольной прямой отрезок АЕ=ае и описать из точки А радиусом, равным аb , и из точки Е радиусом, равным bе, дуги окружностей до взаимного пересечения в точке В. - Соединить точку В с точками А и Е – получится треугольник АВЕ, равный треугольнику аbе. - Таким же способом триангуляции построить треугольники ВDЕ и ВСD , равные соотвественно треугольникам bdе и bсd. Построенный пятиугольник АВСDЕ будет равен данному пятиугольнику аbсdе. - Таким же способом можно построить любой многоугольник, равный данному.

Построения, связанные с углами

Деление угла на равные части

1.4.1.1 Разделить угол на две равные части (провести биссектрису угла):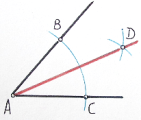
1.4.1.2 Разделить прямой угол на три равные части (трисекция прямого угла)

Построение углов

1.4.2.1 Построение угла, равного данному
1.4.2.2 Построение прямого угла
1.4.2.3 Построение углов,кратных 15 ⁰
1.4.2.4 Построение углов, кратных 30 ⁰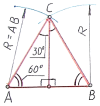
1.4.2.4 Построение разных углов

Применение геометрических построений-см. Приложение А1.

Построение плоских кривых с помощью циркуля

Циркульные кривые

Окружность

Рис.3 Рис.4 Рис.5 Рис.6

Окружность — замкнутая плоская кривая, которая состоит из всех точек на плоскости, равноудалённых от заданной точки О. Эта точка называется центром окружности(см.рис.3). Отрезок, соединяющий центр с какой-либо точкой окружности, называется радиусом (R). Отрезок секущей, расположенный внутри окружности, называется хордой. Хорда – отрезок, соединяющий любые две точки окружности. Хорда, проходящая через центр окружности, называется диаметром. Диаметр вдвое больше радиуса: он делит окружность на две равные части и поэтому является её осью симметрии. Диаметр больше любой другой хорды. Любые две не совпадающие точки окружности делят её на две части. Каждая из этих частей называется дугой окружности. Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром. Прямая, имеющая с окружностью ровно одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности. Касательная к окружности всегда перпендикулярна её радиусу (и диаметру), проведенному в точке касания. Практическое построение окружности производится с помощью циркуля.

Окружность называется описанной вокруг многоугольника в том случае, если все вершины многоугольника лежат на этой окружности (см.рис.4 ).

Окружность называется вписанной в многоугольник, если все стороны многоугольника касаются этой окружности, а многоугольник называется описанным около этой окружности (см.рис.5 ).

Центральный угол - это угол, вершина которого находится в центре окружности (см.рис.6).

Коробовые кривые.

2.1.2.1 Овалы (См. Приложение Б1).

2.1.2.2 Овоиды (См. Приложение Б2).

2.1.3 Своды(См. Приложение Б3).

2.1.4 Завитки(См. Приложение Б4).

2.1.5 Архитектурные обломы(См. Приложение Б5).

Лекальные кривые

Существует большое количество лекальных кривых. Для исследования взяты кривые сечения конуса, циклические кривыеи линия изогнутой гибкой рейки.

Точное построение кривых сечений конуса выполняется с помощью циркуля (см.табл.1).

Произвольные кривые сечения конуса можно выполнить и без помощи циркуля. Например, зная определение эллипса, можно сделать простейший прибор, вычерчивающий эллипс (см.рис.7). Для этого надо два гвоздика вонзить в чертёжную доску, надеть на них кольцо из нитки,а карандаш двигать по бумаге так, чтобы он всё время натягивал нитку. Тогда кончик грифеля будет рисовать на бумаге эллипс.

Рис.7

Кривые сечения конуса

Таблица 1

2.2.1.1 Эллипс		Параметры АВ и СD (задаются) – большая и малая оси, взаимно перпендикулярны, делятся пополам точкой О – центром эллипса. Положение фокусов F₁ и F₂ на большой оси определяется засечками дуги радиусом ОА=АВ:2, проведённой из точки С или D. Эллипс обладает таким свойством: сумма расстояний от каждой точки М, N… до фокусов постоянна и равна большой оси эллипса: F₁М и F₂М = F₁N + F₂N. Эта формула – математический закон, которому подчиняются все точки эллипса.
2.2.1.2 Пара-бола		Х – ось параболы (линия симметрии); F – фокус; l – (директриса) прямая линия, перпендикулярная к оси Х; P=OF – параметр параболы (задаётся); А – вершина (точка пересечения оси Х с ветвью параболы), ОА=Р:2=ОF:2.
2.2.1.3 Гипер-бола		О – центр; 2а – параметр (задаётся); X и Y – две взаимно перпендикулярные оси симметрии, Х – главная (действительная) ось; Y – малая (мнимая) ось; А и В – вершины гиперболы; F₁ и F₂ - фокусы гиперболы; Асимптоты – две прямые, к которым гипербола стремится, но никогда с ними не пересекается.

После кривых сечений конуса можно обратиться к циклическим кривым (см.рис.8, 9,10).

Рис.8 Циклоида

Рис.9 Гипоциклоида

Рис.10 Эпициклоида

Как их различать? Приклеим белый круг на обод велосипедного колеса и поедем по ровному асфальту. За один оборот колеса точка опишет одну ветвь циклоиды. Теперь для сравнения приложим к верхнему краю линейки обруч (см.рис.11а), к которому прикрепили карандаш и который нужно катить по линейке. Карандаш будет вычерчивать кривую – тоже циклоиду (см.рис.11б), что по-гречески значит «кругообразная». Определяется она как кривая, которую описывает точка обода колеса, катящегося без проскальзывания по прямой линии.

а) б)

Рис.11

Теперь на велосипеде с помеченной точкой проедем по яме, представляющей в разрезе дугу окружности – точка опишет гипоциклоиду.

Гипоциклоида – плоская кривая, описываемая точкой производящей окружности, которая без скольжения катится по направляющей окружности, при этом направляющая и производящая окружности имеют внутреннее касание (см.рис12).

Рис.12 Рис.13

И ещё раз проедем, только теперь по небольшому холмику, представляющей в разрезе тоже дугу окружности – точка опишет эпициклоиду.

Эпициклоида – плоская кривая, описываемая точкой производящей окружности, которая без скольжения катится по направляющей окружности, при этом производящая и направляющая окружности имеют внешнее касание (см.рис.13).

При точном построении находятся точки, по которым и обводятся циклические кривые. Основной инструмент здесь лекало, они поэтому так и называются- лекальные кривые, но циркуль здесь главный помощник.

Давно математики пытались решить такую задачу: какой формы должен быть гладкий жёлоб, соединяющий две точки А и В (А выше, чем В), чтобы гладкий металлический шарик скатился по этому желобу из точки А в точку В под действием своего веса за кратчайшее время? Можно подумать, что жёлоб должен быть прямолинейным. Но это не так. Может быть, следует выгнуть по дуге окружности, как думал великий итальянский физик, астроном и математик Галилео Галилей, живший на рубеже XVI – XVII вв.? Нет, Галилей ошибался. Только в 1696 г. швейцарский математик Иоганн Бернулли установил, что желоб должен быть выгнут по циклоиде, опрокинутой вниз (см.рис.14, 15).

Рис.14

Рис.15

Для того, чтобы подтвердить это, был проведён эксперимент. Вместо жёлоба была взята полиэтиленовая труба (она имеет свойство сгибаться). Для чистоты эксперимента, чтобы согнуть трубу по циклоиде, на четырёх листах ватмана была построена половина циклоиды с исходным диаметром 95 см.

Сначала засекалось время скатывания шарика по кривой линии (см.рис.16), потом – по циклоиде (см.рис.17) и последнее – по прямой (см.рис.18).

Рис.16 Рис.17 Рис.18

В результате эксперимента выявлено время движения шарика по разным видам трассы (см.табл.2).

Таблица 2 Время движения шарика по трассе

Линия прохождения трассы	Длина трассы L, см	Время прохождения трассы t, с	Место
Кривая	402,0	1,09	II
Циклоида	386,6	0,95	I
Прямая	298,3	1,27	III

Результат эксперимента подтвердил, что скорость прохождения по трассе минимальная в том случае, когда трасса выполнена в виде циклоиды, перевёрнутой вниз: 0,95 секунды при условии, что длина трассы по циклоиде гораздо длиннее, чем по прямой и чуть меньше, чем по кривой. Это должно учитываться при сооружении спортивных трасс.

И ещё одна, последняя из исследуемых лекальных кривых, - линя изогнутой гибкой рейки. На рис.19 показано построение формы купола. Кривая его очерка представляет собой сочетание двух кривых, отображающих различные условия работы материала (линия О-2 – растяжение, линия 2-1-3 – сжатие). Последний участок выражает линию равного сопротивления – очертание изогнутой гибкой рейки.

Рис.19 Рис.20

Рассмотрим графическое построение линии изогнутой рейки (см.рис.20).На прямой линии выбирают точку О – полюс и вершину А кривой. Вычерчивают окружность, центр которой лежит на прямой ОА. На отрезке АВ проводят ряд прямых, перпендикулярных ему. Из точки В проводят лучи к точкам пересечения параллельных прямых с окружностью (точки 1₀, 2₀, 3₀, 4₀), а из точки О проводят лучи, параллельные соответствующим лучам первого пучка, также до пересечения с параллельными прямыми. Получим искомые точки 1, 2, 3, 4.

Величина параметраa относительно диаметра окружности определяет степень изгиба, если он уменьшается – изгиб увеличивается. Для того, чтобы подтвердить это, будем менять параметр a (см. рис.21-23). Действительно, исследование подтверждает, что при увеличении параметра aизгиб уменьшается (см. рис.21), а при уменьшении – увеличивается (рис.23).

Рис.21 Рис.22 Рис.23

И ещё одна закономерность выявлена при исследования линии изогнутой гибкой рейки: если поменять параметрa и радиус (или диаметр) исходной окружности в одинаковой пропорции (принят к=1,5 на чертеже), то изгиб получается примерно одинаковым (см. рис.24).

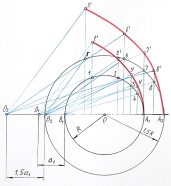Рис.24

Заключение

В исследовательской работе «Что умеет школьный циркуль?» чётко прослеживаются три этапа - основные направления, выполняемые с помощью циркуля: геометрические построения, циркульные и лекальные кривые и их применение.

На первом этапе, вгеометрических построениях,выявлено, что при построении параллельных прямых можно в одном случае построить параллелограмм, во втором – ромб, в третьем – трапецию, а в четвёртом случае – соответственные углы (см.п.1.1.3.2). Даны примеры применения геометрических построений в геометрии, черчении и технике.

На втором этапеисследованы циркульные кривые и построениес их помощью геометрических тел и развёрток. Исследовано применение циркульных кривых в покрытиях зданий, в арках, колоннах, в архитектуре Кемеровской области (см. Приложение Б8 - Б11).

На третьем этапе исследовательской работы для исследования лекальных кривых выбраны кривые сечения конуса, циклические кривые и линия изогнутой гибкой рейки.

Особый интерес из кривых сечений конуса вызвала парабола. Проведено исследование дальности полёта шарика в зависимости от угла наклона дула детского пистолета (см. Приложение В2). В результате исследования выявлено, что дальность полёта (по параболе) шарика максимальная, если угол наклона дула составляет 45⁰. Это свойство можно использовать на уроках физкультуры при метании спортивных снарядов: мяча, гранаты, ядра, копья.

При исследовании циклических кривых был проведён эксперимент, который подтвердил вывод Бернулли о том, что кратчайшее время скатывания шарика с верхней точки А в нижнюю точку В по наклонной под действием собственного веса должно быть по циклоиде, опрокинутой вниз.

При исследовании изогнутой гибкой рейки показано, что при уменьшении заданного параметра увеличивается её изгиб. Это свойство применяется при конструировании энтазиса в колоннах (изгиб минимальный), в луковичных главах храмов и в покрытиях зданий, называемых «бочкой» или «крещатой бочкой», где изгиб максимальный.

Поставленная цель работы: выявление построений с помощью циркуля и применения этих построений – достигнута.

Гипотеза доказана: Если уметь чертить с помощью циркуля, можно таким образом решать различные задачи, строить чертежи, научиться видеть в окружающем нас мире удивительный мир геометрических фигур.

Дата добавления: 2018-08-06; просмотров: 2230; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 567 8 9 Следующая ⇒

Мы поможем в написании ваших работ!