Способы составления характеристического уравнения
О корнях характеристического уравнения
1. Алгебраизация однородного уравнения цепи для свободных составляющих.
1). Система уравнений цепи сводится к одному уравнению для конкретной функции 
.
2). Отбрасывая правую часть (т.е. исключая из схемы внешние источники), записывают однородное уравнение для свободной составляющей 
.
Для рассмотренной выше схемы (Рис. 1.8 §2) запишем уравнение для тока 
:
3). Характеристическое уравнение является результатом алгебраизации этого однородного уравнения.
Обозначив, оператор дифференцирования, как 
и 
, запишем:
После сокращения на ток 
получается характеристическое уравнение:
или
Корни этого уравнения 
и 
и будут показателями степени в решении 
для нашего примера.
Содержание характеристического уравнения.
В характеристическом уравнении параметры цепи связаны между собой посредством оператора дифференцирования 
.
2. То же характеристическое уравнение получится, если изменить последовательность операций.
1). Из схемы исключаются источники.
2). Записывается система уравнений для свободных функций 
.
3). Производится алгебраизация уравнений системы.
4). Система уже алгебраизованных уравнений сводится к одному уравнению.
Проделаем эти операции для рассматриваемого примера (Рис . 1.12)
Рис. 1.12
|
Алгебраизация интегральных слагаемых производится следующим образом:
|
|
|
Если 
, то 
, 
или 
. Следовательно, как результат формальных математических операций имеем:
.
Алгебраизованная система примет вид:
Сведем ее к функции тока 
:
После сокращения на 
получается то же самое характеристическое уравнение.
, т.е.
3. Сопоставим алгебраизованную систему с уравнениями цепи без источников для синусоидального установившегося режима в комплексах действующих значений (Рис. 1.13).
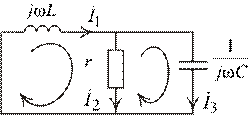Рис. 1.13
|
Коэффициенты алгебраизованной системы отличаются от коэффициентов в синусоидальном установившемся режиме только тем, что вместо сомножителя 
записан оператор дифференцирования .
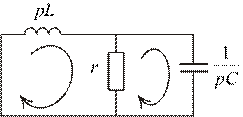Рис. 1.14
|
Тогда правомерно говорить и об алгебраизованной схеме цепи с исключенными источниками, где вместо комплексных сопротивлений 
рассматриваются аналогичные конструкции 
(Рис 1.14).
4. Характеристическое уравнение можно получить, не сворачивая систему алгебраизованных уравнений для свободных составляющих, приравняв к нулю ее главный определитель.
Физически в реальной цепи всегда существует свободный процесс. Значит, существует решение для свободных составляющих 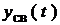. Но тогда существует и решение системы однородных алгебраизованных уравнений. Смысловое содержание ее решений не обсуждается, но необходимым условием существования ненулевых решений для такой системы является равенство нулю ее главного определителя.
|
|
|
Приравняв к нулю главный определитель этой системы 
, мы получим конструкцию, которая связывает параметры схемы посредством оператора дифференцирования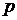 
, то есть получим, то же самое характеристическое уравнение.
Для рассматриваемой нами системы
,
или:
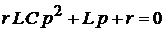
Проведенные здесь рассуждения позволяют сделать целый ряд принципиально важных заключений.
1.) Равенство 
необходимо ля существования свободного тока (или других функций) в любой ветви схемы. Значит, характеристическое уравнение для любых функций одинаково. Можно вообще говорить о характеристическом уравнении цепи.
2.) А если так, то, обращаясь к первому способу составления характеристического уравнения заключаем, что уравнения цепи, составленные для любых функций в своей левой части одинаковы (коэффициенты, конструирующие характеристическое уравнение одни и те же). Отличаются уравнения для разных функций только свободными членами (правые части разные).
3.) Корни характеристического уравнения являются показателями степени в решениях 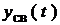. Они одинаковы для всех функций. Значит, переходный процесс для всех функций протекает (затухает, как мы далее увидим) синхронно.
|
|
|
5. Систему независимых контуров в схеме всегда можно выбрать так, чтобы в любой интересующей нас ветви ток был равен только одному контурному току. Значит, для существования ненулевого решения необходимым условием является равенство нулю главного определителя алгебраизованной системы контурных уравнений. Он легко составляется по алгебраизованной схеме с исключенными источниками. В нашем примере:
6. Токи в ветвях выражаются через потенциалы узлов. Ненулевое решение обязано нулевому значению главного определителя системы узловых уравнений алгебраизованной системы. В нашем примере с одним независимым узлом он вырождается в единственную собственную узловую проводимость.
7. И еще один способ – через входное сопротивление алгебраизованной пассивной схемы относительно точек разрыва произвольной ветви.
Рассмотрим сначала ситуацию с синусоидальным режимом.
Исключим источники, разорвем первую ветвь и подведем к точкам разрыва напряжение 
. Запишем решение системы контурных уравнений для первого контурного тока, равное току 
на входе цепи:
|
|
|
.
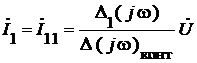Здесь только одно слагаемое, т.к. в схеме единственный источник.
Входное сопротивление схемы:
пропорционально главному определителю системы контурных уравнений.
Значит, в ситуации алгебраизованной схемы 
.
Если 
, то равенство 
также является характеристическим уравнением цепи.
Рис. 1.15
|
;
;
.
Приведенные рассуждения справедливы для точек разрыва любой ветви алгебраизованной схемы с исключенными источниками. Значит, построив такую схему, можно разорвать любую ветвь, и, приняв к нулю входное сопротивление, относительно точек разрыва прийти к тому же характеристическому уравнению.
Рис. 1.16
|
Рис. 1.17
|
И, наконец:
8. Здесь рассмотрены семь способов формирования характеристического уравнения. Корнями этого уравнения определяется характер переходного процесса (форма всех переходных функций). И с какой бы точки зрения мы не рассматривали цепь, мы увидим всегда одну и ту же ее физическую данность, одни и те же ее характеристики.
В цепях, где система уравнений разваливается (например, при наличии короткозамкнутых ветвей), из изложенных в этом параграфе фундаментальных положений могут быть исключения.
9. В решении 
все слагаемые затухают. Ни одно слагаемое не возрастает до бесконечности, все стремятся к нулю. В нормальной цепи с исключенными источниками запасенная в накопителях энергия 
и 
израсходуется на тепловые потери в активных сопротивлениях. Значит, действительные корни характеристического уравнения всегда отрицательны. У комплексно-сопряженных корней будут отрицательными их действительные части.
|
Рис. 1.18
Дата добавления: 2018-06-27; просмотров: 800; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!