Уравнение вращательного движения твёрдого тела вокруг неподвижной оси.
Уравнение вращательного движения твердого тела вокруг неподвижной оси как системы материальных точек
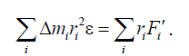
Сумма моментов внешних сил, действующих на тело, равна моменту результирующей этих сил относительно оси OO′:
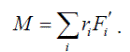
Кинетическая энергия и работа при вращении твёрдого тела вокруг неподвижной оси.
Каждая точка движется с линейной скоростью υi=ωri, тогда кинетическая энергия точки
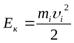или 
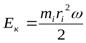
Полная кинетическая энергия вращающегося твердого тела равна сумме кинетических энергий всех его материальных точек:
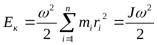(3.22)
(J - момент инерции тела относительно оси вращения)
При вращении твёрдого тела его потенциальная энергия не изменяется, поэтому элементарная работа внешних сил равна приращению кинетической энергии тела:
dA = dE или 
Учитывая, что Jβ = M, ωdr = dφ, имеем α тела на конечный угол φ равна
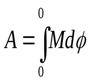(3.25)
При вращении твёрдого тела вокруг неподвижной оси работа внешних сил определяется действием момента этих сил относительно данной оси. Если момент сил относительно оси равен нулю, то эти силы работы не производят.
Гармонические колебания. Смещение, скорость, ускорение при гармонических колебаниях. Период колебания.
Это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса. Уравнение гармонического колебания устанавливает зависимость координаты тела от времени
|
|
|
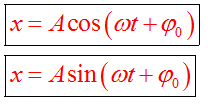
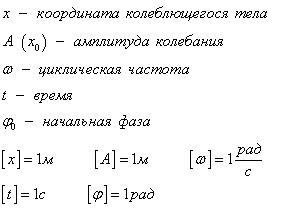
Согласно определению скорости, скорость – это производная от координаты по
Скорость при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания скорости опережают колебания смещения по фазе на p/2.
Величина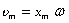 
- максимальная скорость колебательного движения (амплитуда колебаний скорости).
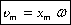
Следовательно, для скорости при гармоническом колебании имеем: 
,
а для случая нулевой начальной фазы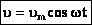 
(см. график).
Согласно определению ускорения, ускорение – это производная от скорости по времени:
-
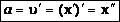вторая производная от координаты по времени. Тогда: 
.
Ускорение при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания ускорения опережают колебания скорости на p/2 и колебания смещения наp(говорят, что колебания происходятв противофазе).
Величина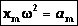 
- максимальное ускорение (амплитуда колебаний ускорения). Следовательно, для ускорения имеем: 
,
а для случая нулевой начальной фазы: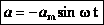 
(см. график).
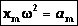
Смещение от положения равновесия при гармонических колебаниях описывается уравнением (его называют кинематическим законом гармонического движения) вида:
|
|
|
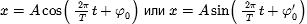
где х — смешение — величина, характеризующая положение колеблющейся точки в момент времени t относительно положения равновесия и измеряемая расстоянием от положения равновесия до положения точки в заданный момент времени; А — амплитуда колебаний — максимальное смещение тела из положения равновесия; Т — период колебаний — время совершения одного полного колебания; т.е. наименьший промежуток времени, по истечении которого повторяются значения физических величин, характеризующих колебание;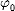 
— начальная фаза.
14. Математический и физический маятники. Период колебаний. Энергия колебаний.
Физическим маятником называется твердое тело, которое может качаться вокруг неподвижной горизонтальной оси. Точка пересечения ее А вертикальной плоскостью, проходящей через центр масс маятника, называется точкой подвеса маятника (рис. 6.3). Положение тела в каждый момент времени можно характеризовать углом отклонения его из положения равновесия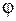 
. Угол 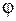играет роль обобщенной координаты q. Кинетическая энергия качающегося физического маятника определяется выражением
,
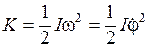где I – момент инерции маятника относительно оси А.
Потенциальная энергия равна
,
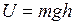где h – высота поднятия центра масс С над его самым нижним положением. Обозначим через а расстояние между центром масс С и точкой подвеса А. Тогда
|
|
|
.
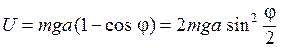В случае малых колебаний синус угла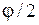 
можно приближенно заменить самим углом. В этом приближении
.
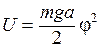Таким образом, для малых колебаний потенциальная и кинетическая энергии приводятся к виду (6.14), причем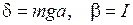 
. Отсюда следует, что малые колебания физического маятника будут приблизительно гармоническими с циклической частотой
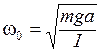(6.18)
и периодом
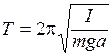. (6.19)
Частным случаем физического маятника является математический маятник. Так называется маятник, вся масса которого практически сосредоточена в одной точке – в центре масс маятника С.
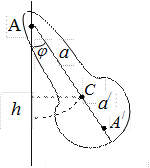
Рис. 6.3
Примером математического маятника может служить шарик, подвешенный на длинной нити. В случае математического маятника
,
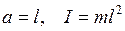где l – длина маятника.
Формула (6.19) переходит в
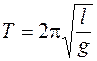. (6.20)
Сравнивая формулы (6.19) и (6.20), заключаем, что физический маятник колеблется так же, как математический маятник с длиной
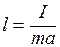, (6.21)
которая называется приведенной длиной физического маятника.
Отложим от точки подвеса А вдоль прямой АС отрезок 
, длина которого равна приведенной длине физического маятника l (см. рис. 6.3). Точка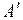 
называется центром качания. Центр качания можно определить как математическую точку, в которой надо сосредоточить всю массу физического маятника, чтобы период его колебаний остался без изменений.
|
|
|
По теореме Штейнера
,
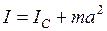где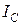 
– момент инерции маятника относительно параллельной оси, проходящей через центр масс С. Подставив это выражение в формулу (6.21), придадим ей вид
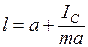. (6.22)
Отсюда следует, во-первых, что l > a, т. е. точка подвеса А и центр качания 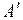лежат по разные стороны от центра масс С и, во-вторых, что всем точкам подвеса, одинаково удаленным от центра масс маятника, соответствует одна и та же приведенная длина l, а следовательно, один и тот же период колебаний T.
Точка подвеса и центр качания являются взаимными или сопряженными точками в следующем смысле. Если маятник подвесить за центр качания 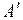, то его период не изменится и прежняя точка подвеса А сделается новым центром качания.
Дата добавления: 2018-06-27; просмотров: 461; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!