Взаимное расположение плоскостей в пространстве. Угол между плоскостями. Двугранный угол. Измерение двугранных углов.
Пусть уравнения A1x + B1y + C1z + D1 = 0, A12 + B12 + C12 ≠ 0 и A2x + B2y + C2 z + D2 = 0,
A22 + B22 + C22 ≠ 0, описывают в одной и той же декартовой системе координат две плоскости, нормальные векторы которых соответственно N1 = (A1, B1, C1) и N2 = (A2, B2, C2). Угол между этими плоскостями — это угол между их нормальными векторами и определяется по формуле
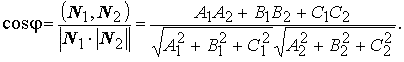
Плоскости совпадают, тогда и только тогда, когда существует отличное от нуля число k такое, что одновременно выполнены равенства A1= kA2 ,B1= kB2 , C1= kC2 , D1= kD2.
Плоскости параллельны, тогда и только тогда, когда существует отличное от нуля число k такое, что одновременно выполнены равенства A1= kA2 ,B1= kB2 , C1= kC2 и D1≠ kD2 (нормальные векторы плоскостей параллельны).
Плоскости перпендикулярны, тогда и только тогда, когда A1A2 + B1B2+ C1C2 = 0 (нормальные векторы плоскостей перпендикулярны).
Угол между плоскостями.
Угол между двумя плоскостями в пространстве j связан с углом между нормалями к этим плоскостям j1 соотношением: j = j1 или j = 1800 - j1, т.е.
cosj = ±cosj1.
Определим угол j1. Известно, что плоскости могут быть заданы соотношениями: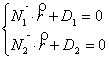 
, где 
(A1, B1, C1),
(A2, B2, C2). Угол между векторами нормали найдем из их скалярного произведения: 
. Таким образом, угол между плоскостями находится по формуле: 
Определение 1. Двугранным углом называется часть пространства, ограниченная двумя полуплоскостями, границей каждой из которых служит их общая прямая. Двугранный угол также называют углом между данными плоскостями.
|
|
|
Определение 2. Плоскости (полуплоскости), которые ограничивают двугранный угол, называются гранями двугранного угла.
Определение 3. Линия пересечения граней двугранного угла называется ребром двугранного угла.
Определение 4. Линейным углом двугранного угла называется угол, образованный двумя полупрямыми, полученными при пересечении граней двугранного угла плоскостью, перпендикулярной ребру этого двугранного угла. Значение линейного угла данного двугранного угла есть значение данного двугранного угла.
Взаимное расположение плоскостей в пространстве. Многогранный угол. Трехгранный угол. Их свойства.
Пусть уравнения A1x + B1y + C1z + D1 = 0, A12 + B12 + C12 ≠ 0 и A2x + B2y + C2 z + D2 = 0,
A22 + B22 + C22 ≠ 0, описывают в одной и той же декартовой системе координат две плоскости, нормальные векторы которых соответственно N1 = (A1, B1, C1) и N2 = (A2, B2, C2). Угол между этими плоскостями — это угол между их нормальными векторами и определяется по формуле
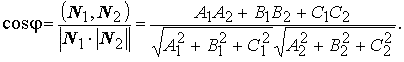
Плоскости совпадают, тогда и только тогда, когда существует отличное от нуля число k такое, что одновременно выполнены равенства A1= kA2 ,B1= kB2 , C1= kC2 , D1= kD2.
|
|
|
Плоскости параллельны, тогда и только тогда, когда существует отличное от нуля число k такое, что одновременно выполнены равенства A1= kA2 ,B1= kB2 , C1= kC2 и D1≠ kD2 (нормальные векторы плоскостей параллельны).
Плоскости перпендикулярны, тогда и только тогда, когда A1A2 + B1B2+ C1C2 = 0 (нормальные векторы плоскостей перпендикулярны).
Определение 5. Фигура, образованная тремя лучами (ребрами), исходящими из одной точки (вершины) и не лежащими в одной плоскости, и тремя частями плоскостей (гранями), заключенных между этими частями, нахывается трехгранным углом.
Определение 6. Грань трехгранного угла называется также плоским углом трехгранного угла.
Определение 7. Двугранные углы, образованные гранями трехгранного угла, называются двугранными углами трехгранного угла.
Признаки равенства трехгранных углов:
Теорема 1. Если плоские углы двух трехгранных углов соответственно равны, то такие трехгранные углы равны.
Теорема 2. Если в трехгранных углах соответственно равны по два плоских угла и двугранные углы, заключенные между их гранями, то такие трехгранные углы равны.
Теорема 3. Если в трехгранных углах соответстввенно равны по два двугранных угла и плоские углы в (общей) прилежащей к ним грани, то такие трехгранные углы равны.
Теорема 4. Два трехгранных угла, у которых равны соответственные двугранные углы, равны 
между собой.
|
|
|
Теорема 5. Теорема синусов. Синусы двугранных углов трехгранного угла пропорциональны синусам плоских углов соответственно противороложных граней трехгранного угла.
Теорема 6. Двугранные углы трехгранного угла можно найти через его плоские углы с помощью следующей формулы:
Доказательство. Отложим на ребре а отрезок ОА=1 и проведем нормальное сечение АВС двугранного угла а. Из прямоугольного треугольника ОАВ находим АВ=tgÐab; OB=secÐab. Также имеем AC=tgÐac, OC=secÐac.
Для ВС находим по теореме косинусов, примененной к треугольнику ВАС (для краткости плоские углы обозначаем просто ab, bc, ac, двугранные - a, b, c):
ВС2=tg2ab+tg2ac-2tgab×tgac×cosa.
Теперь применим теорему косинусов к треугольнику ВОС:
ВС2=sec2ab+sec2ac-2secab×secac×cosbc.
Получим, sec2ab+sec2ac-2secab×secac×cosbc = tg2ab+tg2ac-2tgab×tgac×cosa или
1+tgab×tgac×cosa=secab×secac×cosbc. Отсюда находим
cosbc = cosab×cosac+sinab×sinac×cosa Аналогично cosac = cosab×cosbc+sinab×sinbc×cosb cosab =
cosbc×cosac+sinbc×sinac×cosc
Теорема 7. В трехгранном угле каждый плоский угол меньше суммы двух других.
Теорема 8. Сумма плоских углов трехгранного угла меньше четырех прямых.
Теорема 9. Если два плоских угла трехгранного угла равны, то перпендикуляр, проведенный к третей грани из точки принадлежащей общему ребру равных граней, упадет на биссектрису третьего плоскосго угла.
|
|
|
Возьмем на ребре а точку К. Из точки К опустим на грань bc перпендикуляр КН. Также опустим из точки К перпендикуляры КА и КВ на ребра b и c соответственно. Теперь соединим точку Н с точками А и В. Прямые НА и НВ соответственно перпендикулярны ребрам b и c по теореме о трех перпендикулярах.
Треугольники СКА и СКВ прямоугольны и равны по гипотенузе и острому углу, поэтому КА=КВ.
Треугольники АКН и ВКН прямоугольны и равны по гипотенузе и катету. поэтому НВ=НА.
Треугольники АСН и ВСН равны по катету и гипотенузе, поэтому углы АСН и ВСН равны, а прямая СН является биссектрисой угла С.
Определение 8. Несколько плоскостей, пересекающихся в одной точке, разбивают пространство на части, кадая из которых может быть названа многогранным углом.
Дата добавления: 2018-05-13; просмотров: 684; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!