Окружность, вписанная в треугольник. Формулы, связывающие элементы треугольника с радиусом вписанной окружности

Окружность называется вписанной в треугольник, если она касается всех его сторон.

Теорема. Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис. Доказательство. Пусть ABC данный, O – центр вписанной в него окружности, D, E и F – точки касания окружности со сторонами. Δ AEO = Δ AOD по гипотенузе и катету (EO = OD – как радиус, AO – общая). Из равенства треугольников следует, что ∠ OAD = ∠ OAE. Значит AO биссектриса угла EAD. Точно также доказывается, что точка O лежит на двух других биссектрисах треугольника. n

Удобно уметь вычислять площадь, если даны три стороны.

Так как S_D = 0,5ah_a; h_a = , где р – полупериметр треугольника; поэтому, S_D = . Эта формула была известна еще в древнем мире и носит название формулы Герона.

Рис. 4

Если знать эту формулу, то любую высоту треугольника удобно вычислять, посчитав предварительно площадь треугольника.

Выведем формулу, связывающую площадь треугольника с радиусом описанной окружности. Так как S_D = 0,5ab×sing и , то S_D = .

По этой формуле бессмысленно вычислять площадь треугольника. Эту формулу можно применить для вычисления радиуса окружности, описанной около треугольника с данными сторонами.

Выведем формулу, связывающую площадь треугольника с радиусом вписанной окружности (см. рис. 4).

S_D = S_AOB + S_BOC + S_COA = 0,5cr + 0,5ar + 0,5br = pr.

 

Также существует формула: , где  - высоты треугольника

 

 

Окружность, описанная около треугольника. Формулы, связывающие элементы треугольника с радиусом описанной окружности

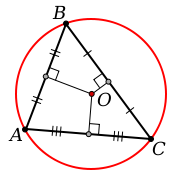Окружностью называется фигура, состоящая из множества точек плоскости, расположенных на одинаковом расстоянии от некоторой точки О этой же плоскости, называемой центром окружности, а отрезок, соединяющий центр с какой-либо точкой окружности, — радиусом окружности. Окружность называется описанной около треугольника, если она проходит через все его вершины.

Вокруг любого треугольника можно описать окружность, притом только одну. Её центром будет являться точка пересечения серединных перпендикуляров.

Доказательство. Пусть ABC – данный треугольник и O – центр окружности описанной около данного треугольника. Δ AOB – равнобедренный ( AO = OB как радиусы). Медиана OD этого треугольника одновременно является его высотой. Поэтому центр окружности лежит на прямой, перпендикулярной стороне AC и проходящей через ее середину. Так же доказывается, что центр окружности на перпендикулярах к другим сторонам треугольника.     Ч.т.д.

Докозательство 2способ

Пусть a и b – серединные перпендикуляры к сторонам AC и BC треугольника ABC, а точка O – точка их пересечения. Из свойств серединного перпендикуляра AO = OC = OB. Следовательно, точка O лежит на серединном перпендикуляре к стороне AB. Таким образом, серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. Кроме того, точка пересечения серединных перпендикуляров равноудалена от вершин треугольника. Отсюда, по определению, центром описанной окружности является точка пересечения серединных перпендикуляров к сторонам треугольника. Теорема доказана.  Ч.т.д.

У остроугольного треугольника центр описанной окружности лежит внутри, у тупоугольного— вне треугольника, у прямоугольного— на середине гипотенузы.

Остроугольный

Тупоугольный

Прямоугольный

3 из 4 окружностей, описанных относительно серединных треугольников (образованных средними линиями треугольника), пересекаются в одной точке внутри треугольника. Эта точка и есть центр описанной окружности основного треугольника.

Центр описанной около треугольника окружности служит ортоцентром треугольника с вершинами в серединах сторон данного треугольника.

Расстояние от вершины треугольника до ортоцентра вдвое больше, чем расстояние от центра описанной окружности до противоположной стороны.

Радиус описанной окружности может быть найден по формулам

                            

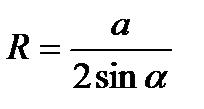
Где:a,b,c — стороны треугольника, α — угол, лежащий против стороны a, S — площадь треугольника.

 

 

Прямая Эйлера

Т1. Пусть О — центр окружности, описанной около треуголь­ника ABC, М — точка пересечения его медиан, Н — орто­центр. Тогда точки О, М, Н лежат на одной прямой, причем М делит отрезок ОН в отношении 2:1, считая от Н. Прямая, содержащая эти точки, называется прямой Эйлера для треугольника ABC. Дано: ∆АВС, ВB₁┴АС, СС₁ ┴АВ, Н = ВB₁∩ СС₁, АА₂, ВВ₂ — медианы ∆АВС,
М = АА₂ ∩ВВ₂. В₂О┴АС, А₂О┴ВС, О = В₂О ∩ А₂О (см. рис.). Доказать: М ОН, МН=2ОМ.

Доказательство.Пусть М₁, = ОН∩ВВ₂.

Тогда ∆М₁ОВ₂ ~ ∆M₁HB , так как OM_lB₂ = HM₁B (как вертикаль­ные), OB₂M₁ = M₁BH (как накрест лежащие при параллельных прямых ОВ₂ и ВВ₁ и секущей В₂В ). Из подобия треугольников ОМ₁В₂ и НМ₁В получаем: . Отношение ОВ₂: ВН = 1:2, так как расстояние от центра описанного круга О до стороны ВС вдвое меньше, чем расстояние от вершины В до ортоцентра Н. Тогда из (1) получаем . Но если медиана делится точкой в отношении 2:1, считая от верши­ны треугольника, то это точка — центроид треугольника, т.е. точка совпадает с точкой М. А это означает, что точки Н М, О лежат на одной прямой, так как точкой М₁ мы обозначили точку пересече­ния ОН с медианой ВВ₂.Из (1) имеем  _.Так как = М , то n

Окружность Эйлера

РРис. 6.12

Теорема 6.14. В любом треугольнике основания высот, середины сторон и середины отрезков, соединяющих ортоцентр с вершина­ми, лежат на одной окружности.

Окружность носит название окружности девяти точек или окружно­сти Эйлера.

Дано: АВС, А1 — середина ВС, В1 — середина АС, С1 — середина АВ, ВН₂ перпендик. АС, Н₂€АС, АН₁перпенд.ВС, H1,€ВС, СН₃перп.АВ, H₃ €АВ, АH1пересеч. ВH₂ и с СH₃ = Н , А₂ — середина АH, В₂ — середина ВH, С₂ — середина СH (рис. 6.11). Доказать: А1, В1, С1, H1, H₂, H₃, A2, В₂, С₂ — лежат на окружности.

Доказательство.

1) Рассмотрим четырехугольник A2C1A1C2. С1А1 — средняя линия ∆АВС .Значит, С1А1 || АС и С1A1 = 1/2АС ;

В

А₂С₂ — средняя линия ∆АНС .Значит, С₂A2|| АС и С2A2 = 1/2 АС . Следовательно, А₂С₁А₁С₂ —параллелограмм.

2) C1,A2 — средняя линия ∆АВH . Значит, С1A2 || ВH . Следовательно, С1A2 1 A2C2 , так как А₂С₂|| АС.

3) Таким образом, С₁А₂С₂А₁ — прямоугольник. Тогда существует ок­ружность, диаметром которой является отрезок С1С₂ (т. е. точка Е— середина С1С₂ — ее центр), которой принадлежат точки А₂, С1, А1, С₂.

4) С₁В₂С₂В1— прямоугольник, так как:

а) С1В1 — средняя линия ∆АВС . Значит, С1В1 || ВС и С1В1 = 1/2ВС.

б) С₂В₂ — средняя линия ∆ВHС . Значит, С₂В₂||  С В и С₂В₂ = 1/2СВ .

в) С1В₂перп.В₂С₂, так как С1В₂|| АH и В₂С₂|| АН .

5) С1С₂ — диаметр окружности (центр окружности Е), описанной около прямоугольника В₁С₁В₂С₂. Таким образом, точки С, В₂, Д, С₂, В1, А2 принадлежат окружности с центром Е и диаметром С,С₂.

6) E— середина диагонали С,С₂ прямоугольников С,A2С₂A1 и С₁В₁С₂В₁. Значит, и вторые диагонали A1А2 и В,В₂ соответственно прямоугольников С,A2С₂A1 и С₁В₂С₂В₁ проходят через точку Е, так как диагонали прямоугольника равны и точкой пересечения делятся пополам. Значит, A1A2 и В,В₂ —тоже диаметры этой окружности.

7) УГОЛ B₂H₂B 1= 90°, так как ВН₂перп. А С, и этот угол опирается на диаметр В₂В, окружности с центром Е. Значит, Н₂ лежит на окружности.

Аналогично угол А2H1A1 = 90° и A1A2 — диаметр окружности. Значит, точ­ка H, лежит на окружности. уголC1H₃C₂ = 90° и С,С₂ — диаметр окруж­ности. Следовательно, точка H₃ принадлежит окружности. Таким образом, все девять точек лежат на окружности. Теорема доказана.

 

Tеорема 6.15. Центр Е окружности девяти точек треугольника лежит на середине отрезка ОН, где Н — ортоцентр треугольника, О — центр описанной окружности, а радиус окружности девяти точек равен половине радиуса описанной около треугольника окружности       

Дано: ∆АВС, A1 — середина ВС, В₁ — середина AC, C1— середина АВ, ВН₂, АН1, СН₃ — высоты треугольника ABC, Н = ВН₂ ∩ АH1∩ СН₃, В₂ — середина ВН, A2 — середина АН;С₂ — середина СН, Е — центр окружности девяти точек, О — центр опи­санной около ∆АВС окружности (рис. 6.12).

Доказать: Е принадл.ОН и ОЕ = EH, ЕА1=1/2R , где R — радиус описанной около ∆АВС окружности.

Доказательство.

1) ∆A1В,С, подобен ∆АВС с коэффициентом подобия к = 1/2

Значит, радиус окружности, описанной около ∆A1B1C1равен 1/2 R. Окружность девяти точек описана около треугольника A1В,С,. Значит, радиус окружности девяти точек равен половине радиуса окружности,

описанной около треугольника ABC, т. е. EA1 = 1/2 R .

2) Треугольники A1B 1C1и А₂В₂С₂ симметричны относительно точки Е (см. доказательство теоремы 6.14). Значит, их ортоцентры тоже симметричны относительно точки Е.

Н — ортоцентр треугольника A2В₂С₂. О — ортоцентр треугольника A1B1C1 так как ОВ1— серединный перпендикуляр к АС, значит, OB1перп. АС,. Аналогично А1О и С10 принадлежат высотам ∆А1В,С,. Таким образом, точки О и Н симметричны относительно точки Е, т. е. ОЕ = ЕН.  Теорема доказана.

Теорема 6.16. Расстояние между центрами О и I описанной и вписанной окружностей треугольника и радиусы R и .r этих окружно­стей связаны формулой: OI² = R² - 2Rr, называемой фор­мулой Эйлера.

Дано: ∆АВС, I— центр вписанной окружности, г — радиус вписанной окружности, О — центр описанной окружности ∆АВС, R — радиус описанной окружности.

Доказать: OI² = R² - 2Rr.

                                              Доказательство.

1) Пусть биссектриса CI угла С треугольника ABC пересекает описан­ную окружность в точке D (рис. 6.13). Проведем диаметр DP этой окружности DP - 2R .

2) Проведем диаметр MN описанной окружности, проходящий через точку /.

Рис. 6.13

Тогда CI*ID = MI*IN (1), так как произведение отрезков хорд, про­ходящих через точку /, — величина постоянная.

3) Обозначим 01 = d . Тогда MI = R + d; IN = R-d . Тогда (1) перепишется в виде: CI*ID = R²-d² (2).

4) ∆APD подобен∆IТС, где IT перп. АС, так как уголPAD = 90° (опирается на диа­метр PD) и уголCTI = 90°; уголAPD = углуACD, как вписанные, опираю­щиеся на дугу AD.

5) Из подобия треугольников APD и ICT имеем: AD/PD =PI/CI ; AD*CI = r-2R (3).

6) В задаче 5.06* доказано, что AD = DI. Тогда (3) перепишем следу­ющим образом: DI - CI = r-2R (4).

7) Из (2) и (4) получаем, что R²-d² = 2Rr, т.е. d²=R²-2Rr, где d=OI ,т. е. OI² = R²-2Rr. Теорема доказана.

Вневписанная окружность.

Опр1. Окружность, касающаяся одной стороны треугольни­ка и продолжений двух других его сторон, называется вневписанной окружностью.

На рис. окружность касается стороны ВС(а) треугольника АВС и продолжений его сторон АС(b) и АВ(с). Центр окружности часто обозна­чают I_а (окружность касается стороны а), а радиус — r_а .

T1. Центр вневписанной окружности треугольника лежит на пересечении биссектрис двух внешних углов и внутренне­го угла треугольника, лежащего против стороны касания с окружностью. Дано: ∆АВС, Доказать: существует I_а — точка пересечения биссектрис углов CAB, МСВ, NBC, где М  АС, МС + СА = AM , N  АВ и NB + ВА = NA . Доказательство: 1)Проведем биссектрису угла CAB. Тогда любая ее точка равноудалена от сторон АС и АВ угла. 2) Проведем биссектрису угла МСВ. Точка I_а пересечения этой бис­сектрисы и биссектрисы угла CAB равноудалена от стороны ВС и продолжений сторон АВ и АС. Значит, точка I_а лежит на биссектрисе угла CBN. 3)Таким образом, I_а — точка пересечения биссектрисы внутреннего угла CAB и двух биссектрис внешних углов МСВ и NBC треугольни­ка AВС.

Если  . n

T2. Точка касания вневписанной окружности треугольника делит его периметр пополам.    Дано: ∆ABC, I_а — центр вневписанной окружности, I_аК — радиус вневписанной окружности, проведенный в точку касания со стороной ВС. Доказать: АС + СК = АВ + ВК. Доказательство. AT = АР, СТ = СК , ВК = BP как отрезки касательных, проведен­ные из одной точки. 2АТ = АТ + АР = AC + СТ + АВ + BP =
=AC + CK + AB + BK = 2P,где P — полупериметр
∆ ABC . Значит, AT = P, но AT = AC + CT =
= AC + CK = P. Таким образом, AC + CK = P =
= AB + BK, т.е. точка К касания вневписанной окружности треугольника делит его периметр пополам. Для любого треугольника можно построить три вневписанные окруж­ности.

Т3. Площадь S треугольника АВС равна . Док-во: n

7. Центроид треугольника

Существование центроида (центра тяжести) треугольника и его основ­ное свойство основано на следующей теореме.

Т1. Три медианы треугольника пересекаются в одной точке М, которая делит каждую из них в отношении 2:1, считая от вершин треугольника.   Дано: ∆ABC, СС₁, АА₁, ВВ₁ — медианы
∆ ABC. Доказать: и

. Д-во: Пусть М — точка пересечения медиан СС₁, АА₁ треугольника ABC. Отметим A₂ — середину отрезка AM и С₂ — середину отрезка СМ. Тогда A₂C₂ — средняя линия треугольника АМС. Значит, А₂ С₂ || АС

и A₂C₂ = 0,5*АС. С₁А₁ — средняя линия треугольника ABC. Значит, А₁С₁ || АС и А₁С₁ = 0,5*АС.

Четырехугольник А₂С₁А₁С₂ — параллелограмм, так как его противо­положные стороны А₁С₁ и А₂С₂ равны и параллельны. Следовательно, А₂М = МА₁  и С₂М = МC₁. Это означает, что точки А₂ и M делят медиану АА₂ на три равные части, т. е. AM = 2МА₂ . Аналогично СМ = 2MC₁. Итак, точка М пересечения двух медиан АА₂ и CC₂ треугольника ABC делит каждую из них в отношении 2:1, считая от вершин треу­гольника. Совершенно аналогично доказывается, что точка пересечения меди­ан АА₁ и BB₁ делит каждую из них в отношении 2:1, считая от вер­шин треугольника.

На медиане АА₁ такой точкой является точка М, следовательно, точка М и есть точка пересечения медиан АА₁ иBB_1.

Таким образом, n

T2. Докажите, что отрезки, которые соединяют центроид с вер­шинами треугольника, делят его на три равновеликие части. Дано: ∆ABC ,  — его медианы.

Доказать: S_AMB = S_BMC = S_AMC. Доказательство.  и высота, проведенная из вершины В, у них общая. 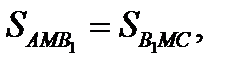т.к. равны их основания  и высота, проведенная из вершины М, у них общая. Тогда

Аналогичным образом доказывается, что S_AMB = S_AMC. Таким образом, S_AMB = S_AMC = S_CMB .n

T3. В треугольнике ABC со сторонами а, b, с , где т_а, т_b, т_с — медианы, при­веденные соответственно к сторонам а, b, с треугольника. Доказательство: 1) Обозначим АА₁ через т_а и вычислим т_а через a, b и с. 2) Продлим АА₁ за точку А₁ на отрезок А₁А₂, равный АА_1. Тогда четырехугольник АВА₂С — параллелограмм, так как его диагона­ли АА₂ и ВС пересекаются и точкой пересечения А₁ делятся пополам. Доказано, что  т.е. .

Откуда .

Аналогично выводятся формулы для .n

 

---

Дата добавления: 2018-05-13; просмотров: 1317; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

⇐ Предыдущая10111213141516171819Следующая ⇒

---

Мы поможем в написании ваших работ!