Обобщающий метод интервалов для решения неравенств
В настоящее время в высшей математике обозначился ряд задач, для решения которых достаточно знаний элементарной математики, но до решения которых не доходит дело в средней школе. Речь идет о методе областей для решения неравенства и системы неравенств с двумя переменными. Приобрести навыки в решении таких неравенств можно, обобщив метод интервалов . Метод интервалов , применяемый для решения неравенств с одной переменной, основывается на свойстве
непрерывности элементарных функций. Суть метода состоит в том, что элементарные функции непрерывны в области своего определения, и изменение знака функции может произойти либо в разрывах области определения, либо в нулях функции. Процесс решения неравенства сводится
к следующим этапам:
· нахождение области определения функции,
· нахождение нулей функции и постановка их на область определения,
· нахождение знаков функции на полученных интервалах.
Покажем, как используя метод аналогий, распространить метод интервалов на тригонометрические неравенства, неравенства с двумя переменными, параметрические неравенства. Применение метода аналогий при обучении преследует несколько целей:
· во-первых, продемонстрировать то, как приемы и методы, дающие решение задачи в одной ситуации, применяются в другой ситуации,
· во-вторых, воспроизведение метода интервалов в изменившихся условиях его применения, приводит к повторению этапов решения и осознанию универсальности метода, каковым он и является на самом деле,
|
|
|
· в-третьих, происходит обучение решению достаточно сложных типов неравенств, умение решать которые помогает освоению разделов высшей математики.
Решения тригонометрических неравенств можно оформлять либо на числовой прямой, что крайне неудобно, либо на тригонометрическом круге. Для того, чтобы подобрать тригонометрические неравенства для демонстрации метода интервалов , можно взять тригонометрическое уравнение, и решение которого предполагает оформление области определения функции и проверку корней уравнения на принадлежность области определения, и преобразовать это уравнение в неравенство. Далее действовать по намеченному плану: найти область определения функции и нанести ее на круг; найти нули функции и нанести их на тот же круг, в итоге круг будет разбит на дуги, на которых
функция сохраняет свой знак. Необходимо проверить знаки функции на полученных дугах. Далее, обходя круг против часовой стрелки, выписать ответ, учитывая периодичность точек на круге.
Прежде чем демонстрировать метод интервалов для решения параметрических неравенств, который называется методом областей, необходимо показать решение неравенства с двумя переменными на плоскости XOY. Построение линий и областей на плоскости ХОУ более привычное дело, чем на плоскости ХО. Чтобы подобрать такие неравенства, можно для начала взять несложное параметрическое неравенство, и заменить параметр на переменную у. Далее вводится в рассмотрение функция двух переменных f(x,y). Областью определения функции двух переменных является либо вся плоскость ХОУ, либо некоторые
|
|
|
части плоскости. Далее функция приравнивается к нулю и строится линия f(x,y)=0, которая разбивает область определения на части, на которых функция сохраняет свой знак. Далее методом пробной точки выбирается произвольная точка из каждой области, ее координаты подставляются в функцию и просчитывается знак функции. Далее выписывается ответ, т.е. прификсированном у, пределы изменения переменной х задаются, как функции
у, либо наоборот. Необходимо отметить, что навыки, приобретенные при выписывании ответа необходимы при расстановке пределов интегрирования в двойном интеграле.
Основные тригонометрические функции, их свойства, графики
Синус
Синусом числа а называется ордината точки, изображающей это число на числовой окружности. Синусом угла в а радиан называется синус числа а. Синус - функция числа x. Ее область определения - множество всех чисел, так как у любого числа можно найти ординату изображающей его точки.
|
|
|
Область значений синуса - отрезок от -1 до 1, так как любое число этого отрезка на оси ординат является проекцией какой-либо точки окружности, но никакая точка вне этого отрезка не является проекцией какой-либо из этих точек. Период синуса равен  . Ведь через каждые
. Ведь через каждые  положение точки, изображающей число, в точности повторяется.
положение точки, изображающей число, в точности повторяется.
Знак синуса: синус равен нулю при 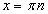 , где n - любое целое число;
, где n - любое целое число;
синус положителен при  , где n - любое целое число;
, где n - любое целое число;
синус отрицателен при  , где n - любое целое число.
, где n - любое целое число.
Синус - функция нечетная. Во-первых, область определения этой функции есть множество всех чисел, а значит,  симметрична относительно начала отсчета. А во-вторых, если отложить от начала два противоположных числа: x и -x, то их ординаты - синусы - окажутся также противоположными. То есть
симметрична относительно начала отсчета. А во-вторых, если отложить от начала два противоположных числа: x и -x, то их ординаты - синусы - окажутся также противоположными. То есть  для любого x.
для любого x.
Синус возрастает на отрезках  , где n - любое целое число.
, где n - любое целое число.
Cинус убывает на отрезке 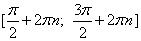 , где n - любое целое число.
, где n - любое целое число.
 при
при  ;
;  при
при  .
.
Косинус
Косинусом числа а называется абсцисса точки, изображающей это число на числовой окружности. Косинусом угла в а радиан называется косинус числа а. Косинус - функция числа. Ее область определения - множество всех чисел, так как у любого числа можно найти ординату изображающей его точки. Область значений косинуса - отрезок от -1 до 1, так как любое число этого отрезка на оси абсцисс является проекцией какой-либо точки окружности, но никакая точка вне этого отрезка не является проекцией какой-либо из этих точек. Период косинуса равен  . Ведь через каждые
. Ведь через каждые  положение точки, изображающей число, в точности повторяется.
положение точки, изображающей число, в точности повторяется.
|
|
|
Знак косинуса:
косинус равен нулю при  , где n - любое целое число;
, где n - любое целое число;
косинус положителен при  , где n - любое целое число;
, где n - любое целое число;
косинус отрицателен при  , где n - любое целое число.
, где n - любое целое число.
Косинус - функция четная. Во-первых, область определения этой функции есть множество всех чисел, а значит,  симметрична относительно начала отсчета. А во-вторых, если отложить от начала два противоположных числа: x и -x, то их абсциссы - косинусы - окажутся равными. То есть
симметрична относительно начала отсчета. А во-вторых, если отложить от начала два противоположных числа: x и -x, то их абсциссы - косинусы - окажутся равными. То есть
 для любого x.
для любого x.
Косинус возрастает на отрезках  , где n - любое целое число.
, где n - любое целое число.
Косинус убывает на отрезках  , где n - любое целое число.
, где n - любое целое число.
 при
при  ;
;  при
при  .
.
Тангенс
Тангенсом числа называется отношение синуса этого числа к косинусу этого числа:  .
.
Тангенсом угла в а радиан называется тангенс числа а. Тангенс - функция числа. Ее область определения - множество всех чисел, у которых косинус не равен нулю, так как никаких других ограничений в определении тангенса нет. И так как косинус равен нулю при  , то
, то  , где
, где 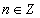 .
.
Область значений тангенса - множество всех действительных чисел.
Период тангенса равен  . Ведь если взять любые два допустимые значения x (не равные
. Ведь если взять любые два допустимые значения x (не равные 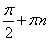 ), отличающиеся друг от друга на
), отличающиеся друг от друга на  , и провести через них прямую, то эта прямая пройдет через начало координат и пересечет линию тангенсов в некоторой точке t. Вот и получится, что
, и провести через них прямую, то эта прямая пройдет через начало координат и пересечет линию тангенсов в некоторой точке t. Вот и получится, что  , то есть число
, то есть число  является периодом тангенса. Знак тангенса: тангенс - отношение синуса к косинусу. Значит, он равен нулю, когда синус равен нулю, то есть при
является периодом тангенса. Знак тангенса: тангенс - отношение синуса к косинусу. Значит, он равен нулю, когда синус равен нулю, то есть при 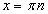 , где n - любое целое число.
, где n - любое целое число.
положителен, когда синус и косинус имеют одинаковые знаки. Это бывает только в первой и в третьей четвертях, то есть при  , где а - любое целое число.
, где а - любое целое число.
отрицателен, когда синус и косинус имеют разные знаки. Это бывает только во второй и в четвертой четвертях, то есть при  , где а - любое целое число.
, где а - любое целое число.
Тангенс - функция нечетная. Во-первых, область определения этой функции симметрична относительно начала отсчета. А во-вторых, 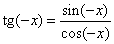 . В силу нечетности синуса и четности косинуса, числитель полученной дроби равен
. В силу нечетности синуса и четности косинуса, числитель полученной дроби равен  , а ее знаменатель равен
, а ее знаменатель равен  , а значит, сама эта дробь равна
, а значит, сама эта дробь равна  . Вот и получилось, что
. Вот и получилось, что  .
.
Значит, тангенс возрастает на каждом участке своей области определения, то есть на всех интервалах вида  , где а - любое целое число.
, где а - любое целое число.
Котангенс
Котангенсом числа называется отношение косинуса этого числа к синусу этого числа:  . Котангенсом угла в а радиан называется котангенс числа а. Котангенс - функция числа. Ее область определения - множество всех чисел, у которых синус не равен нулю, так как никаких других ограничений в определении котангенса нет. И так как синус равен нулю при
. Котангенсом угла в а радиан называется котангенс числа а. Котангенс - функция числа. Ее область определения - множество всех чисел, у которых синус не равен нулю, так как никаких других ограничений в определении котангенса нет. И так как синус равен нулю при 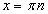 , то
, то  , где
, где  Область значений котангенса - множество всех действительных чисел.
Область значений котангенса - множество всех действительных чисел.
Период котангенса равен периоду тангенса. Ведь если взять любые два допустимые значения x (не равные  ), отличающиеся друг от друга на период тангенса, и провести через них прямую, то эта прямая пройдет через начало координат и пересечет линию котангенсов в некоторой точке t. Вот и получится, что
), отличающиеся друг от друга на период тангенса, и провести через них прямую, то эта прямая пройдет через начало координат и пересечет линию котангенсов в некоторой точке t. Вот и получится, что 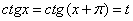 , то есть, что число
, то есть, что число  является периодом котангенса.
является периодом котангенса.
Знак котангенса: котангенс - отношение косинуса к синусу. Значит, он
равен нулю, когда косинус равен нулю, то есть при  .
.
положителен, когда синус и косинус имеют одинаковые знаки. Это бывает только в первой и в третьей четвертях, то есть при  .
.
отрицателен, когда синус и косинус имеют разные знаки. Это бывает только во второй и в четвертой четвертях, то есть при 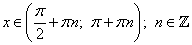 .
.
Котангенс - функция нечетная. Во-первых, область определения этой функции симметрична относительно начала отсчета. А во-вторых,  .
.
В силу нечетности синуса и четности косинуса, числитель полученной дроби равен  , а ее знаменатель равен
, а ее знаменатель равен  , а значит, сама эта дробь равна
, а значит, сама эта дробь равна  .
.
Вот и получилось, что  . Котангенс убывает на каждом участке своей области определения, то есть на всех интервалах вида
. Котангенс убывает на каждом участке своей области определения, то есть на всех интервалах вида  .
.



Дата добавления: 2018-05-13; просмотров: 532; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
