Методы геометрических преобразований. Симметрия. Поворот. Параллельный перенос. Подобие. Гомотетия.
Определение. Движением называется преобразование (т.е. взаимно однозначное отображение плоскости на себя), при котором расстояние между любыми двумя точками равно расстоянию между их образами. Из определения сразу вытекают свойства движений.
1) Движение переводит любую прямую в прямую.
Доказательтво. Пусть точки А, В, С лежат на одной прямой. Тогда АВ + ВС = АС. Из определения движения следует, что образы А', В', С' точек А, В, С удовлетворяют условию А'В' + В'С' = А'С, т. е. точки А', В', С также лежат на одной прямой.
2)Движение переводит любой угол в равный угол.
Доказательство. Из предыдущего свойства следует, что /АОВ переходит при движении в /А'О'В', где А', О', В' — образы точек А, О, В. Но треугольники АОВ и А'О'В' равны по трем сторонам, следовательно, /АОВ = /А'О'В'.
Симметрия
Определение. Симметрией относительно прямой I называется преобразование, переводящее каждую точку А в такую точку А', что прямая I перпендикулярна отрезку АА' и проходит через его середину.
|
|
Утверждение. Симметрия является движением.
Доказательство. Пусть точки А, В переходят в А', В'. Рассмотрим три случая. 1. Отрезок АВ параллелен прямой I. Тогда АВ = А'В', так как АВВ'А' — прямоугольник. 2. Отрезок АВ перпендикулярен прямой I. Искомое равенство получается непосредственным вычислением. 3. Отрезок АВ непараллелен и неперпендикулярен прямой I. Опустим на прямую ВВ' перпендикуляры АС и А'С. Нетрудно убедиться, что точки С и С' симметричны относительно I. Из рассмотрения двух первых случаев следует, что АС = А'С, ВС = В'С'. Поэтому АВ = А'В' как гипотенузы равных треугольников АВС и А'В'С'.
|
|
|
Теорема 1. Любое подобие, сохраняющее ориентацию, с коэффициентом к, отличным от 1, является композицией гомотетии с центром в некоторой точке О и коэффициентом к и поворота вокруг точки О (иногда такое преобразование называется спиральным подобием).
Доказательство. Прежде всего отметим, что справедливо утверждение, обобщающее лемму о двух гвоздях: для любых двух пар различных точек А, В и А', В' существует ровно два подобия, переводящих А в А1 и В в В1. Коэффициент этих подобий равен к = А'В / АВ из них сохраняет ориентацию, а другое меняет. Доказательство этого утверждения полностью повторяет доказательство леммы. Пусть теперь данное подобие переводит точки А, В в А', В'. Если отрезки АВ и А'В' параллельны, данное подобие является гомотетией с центром в точке О пересечения прямых АА' и ВВ' (точки А и В можно выбрать так, чтобы эти прямые не совпадали). В противном случае опишем окружности вокруг треугольников АВО и А'В'Б и найдем вторую точку О их пересечения (если окружности касаются, точки О и О совпадают). Рассмотрев различные случаи расположения точек А, В, А', В', О, О и сравнив углы ОАВ,
|
|
|
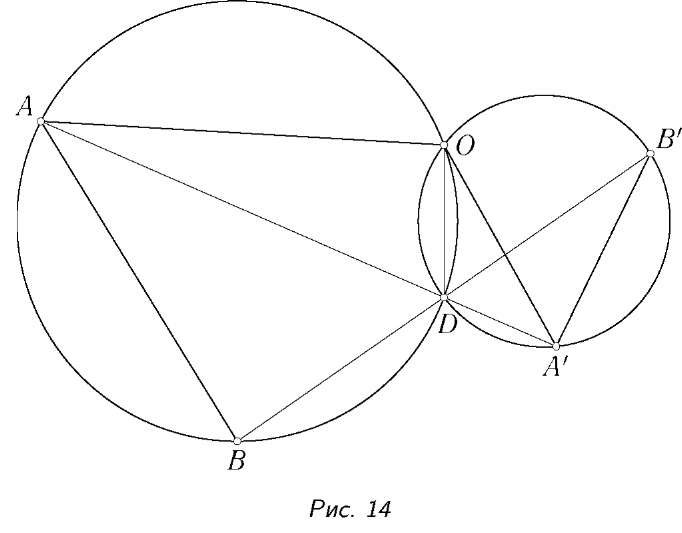
ОйВ, ОБВ', ОА'В', убеждаемся, что углы ОАВ и ОА'В' равны (рис. 14). Аналогично равны углы ОВА и ОВ'А', и, значит, композиция гомотетии с центром О и коэффициентом к и поворота вокруг точки О на угол АОА' переводит А в А', а В в В', т. е. совпадает с данным подобием. Теорема доказана.
Теорема 2. Любое подобие с коэффициентом не равным 1, меняющее ориентацию, можно представить в виде композиции гомотетии с центром в некоторой точке О и симметрии относительно прямой, проходящей через О.
Доказательство. Покажем прежде всего, что данное подобие имеет неподвижную точку. Из теоремы Шаля следует, что оно является композицией гомотетии с центром в произвольной точке и скользящей симметрии. Но композиция гомотетии и параллельного переноса в силу предыдущей теоремы будет гомотетией с тем же коэффициентом, поэтому достаточно рассмотреть подобие, являющееся композицией гомотетии с центром в точке М и коэффициентом к и симметрии относительно прямой I, не проходящей через М. Проведем через М прямую, перпендикулярную прямой I, и введем на ней координаты, так чтобы координата точки М была равна нулю, а координата точки ее пересечения с I единице. Гомотетия с центром в М переводит точку с рис 15 координатой х в точку с координатой кх, а симметрия относительно I переводит точку с координатой кх в точку с координатой 2 — кх. Уравнение х = 2 — кх имеет единственное решение, определяющее неподвижную точку О. Возьмем теперь произвольную точку А, отличную от О, и ее образ А'. Композиция гомотетии с центром в точке О и коэффициентом к и симметрии относительно биссектрисы угла АОА' переводит А в А' и оставляет О на месте, т. е. совпадает с данным подобием (рис. 15). Теорема доказана.
|
|
|
Из теорем 1, 2 следует, что любое подобие, не являющееся движением, имеет ровно одну неподвижную точку. Рассмотрим несколько задач на подобие.
 Определение. Подобием называется преобразование, при котором для любых двух точек А и В отношение расстояний между их образами А' и В' к расстоянию между самими точками равно одному и тому же числу: А'В' = к • АВ. Число к > 0 называется коэффициентом подобия. Из определения сразу следует, что подобия образуют группу. Действительно, композиция подобий с коэффициентами к и к2 будет подобием с коэффициентом к1к2, а преобразование, обратное подобию с коэффициентом к, — подобием с коэффициентом 1/к. Важным частным случаем подобия является гомотетия.
Определение. Подобием называется преобразование, при котором для любых двух точек А и В отношение расстояний между их образами А' и В' к расстоянию между самими точками равно одному и тому же числу: А'В' = к • АВ. Число к > 0 называется коэффициентом подобия. Из определения сразу следует, что подобия образуют группу. Действительно, композиция подобий с коэффициентами к и к2 будет подобием с коэффициентом к1к2, а преобразование, обратное подобию с коэффициентом к, — подобием с коэффициентом 1/к. Важным частным случаем подобия является гомотетия.
|
|
|
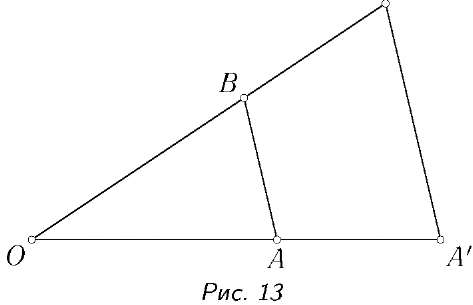
Определение. Гомотетией с центром в точке О и коэффициентом к, отличным от нуля, называется преобразование, переводящее каждую точку А в точку А', лежащую на прямой ОА и удовлетворяющую условию ОА' = к • ОА. При к > 0точки А и А' лежат по одну сторону от точки О,
В' при к < 0 по разные. Отметим, что гомотетия с коэффициентом к = — 1 является центральной симметрией. То, что гомотетия является подобием, почти очевидно. Действительно, если точки А, В переходят в точки А', В', то треугольники ОАВ и ОА'В' подобны и, значит, А'В' = к • АВ (рис. 13). С другой стороны, если дано произвольное подобие с коэффициентом к, то композиция этого подобия и гомотетии с произвольным центром и коэффициентом 1/к будет движением. Поэтому данное подобие можно представить как композицию этого движения и гомотетии с центром О и коэффициентом к. При этом за счет выбора центра гомотетии можно добиться того, что движение будет иметь достаточно простой вид. А именно, верны следующие утверждения.
 Теорема 1. Любое подобие, сохраняющее ориентацию, с коэффициентом к, отличным от 1, является композицией гомотетии с центром в некоторой точке О и коэффициентом к и поворота вокруг точки О (иногда такое преобразование называется спиральным подобием).
Теорема 1. Любое подобие, сохраняющее ориентацию, с коэффициентом к, отличным от 1, является композицией гомотетии с центром в некоторой точке О и коэффициентом к и поворота вокруг точки О (иногда такое преобразование называется спиральным подобием).
Определение.
Параллельным переносом на вектор n называется преобразование плоскости, которое каждую точку А переводит в такую точку А', что АА' = n . То, что параллельный перенос является движением, почти очевидно. Действительно, если точки А, В переходят соответственно в А', В', то из определения параллельного переноса следует, что АА'В'В — параллелограмм и АВ = А'В'. Отметим, что фактически мы доказали более сильное свойство.
Утверждение.
При параллельном переносе любой вектор АВ переходит в равный вектор А'В'.
Следствие.
При параллельном переносе любая прямая переходит в параллельную прямую. Отметим еще два свойства параллельных переносов, непосредственно вытекающие из определения.
1. Композиция параллельных переносов на векторы т и п есть параллельный перенос на вектор т + п.
2. Преобразование, обратное к параллельному переносу на вектор п есть параллельный перенос на вектор n Таким образом, множество всех параллельных переносов является группой.
Поворот
Определение. Поворотом вокруг точки О на угол <р называется преобразование плоскости, переводящее каждую точку А в такую точку А', что ОА = О А' и угол между лучами ОА и О А' (т. е. угол, отсчитываемый против часовой стрелки от луча ОА к лучу ОА') равен у.
Утверждение. Поворот является движением.
Доказательство. Пусть точки А, В переходят соответственно в точки А', В'. Так как /АОА' = /ВОВ', мы заключаем, что /АОВ = = /А'ОВ'. Поэтому треугольники АОВ и А'ОВ' равны по двум сторонам и углу между ними, и, значит, АВ = А'В'. Очевидно, что поворот на угол 2п является тождественным преобразованием. Поэтому всегда можно считать, что 0 ^ у < 2п. Отметим свойства поворота.
1. 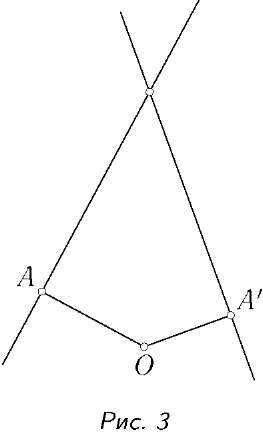 Если прямая а при повороте на угол у переходит в прямую а', то один из углов между а и а' равен у при 0 ^ у < п и у — п при п ^ у < 2п.
Если прямая а при повороте на угол у переходит в прямую а', то один из углов между а и а' равен у при 0 ^ у < п и у — п при п ^ у < 2п.
Доказательство. Если прямая а проходит через центр поворота О, утверждение очевидно. В противном случае опустим на а перпендикуляр ОА и построим образ А' точки А. Так как движения сохраняют величины углов, образом прямой а будет прямая а', проходящая через А' и перпендикулярная ОА'. Из свойств углов с перпендикулярными сторонами вытекает искомое свойство (рис. 3).
2. Композиция поворотов вокруг точки О на углы а и в есть поворот вокруг О на угол а + в (или а + в — 2п).
3. Преобразование, обратное к повороту вокруг точки О на угол у, есть поворот вокруг О на угол 2п — у.
Свойства 2—3 непосредственно следуют из определения поворота. Они означают, что все повороты с данным центром образуют группу. Поворот на угол п называется центральной симметрией. Из свойства 1 вытекает, что центральная симметрия переводит любую прямую в параллельную.
Метод площадей.
Характеристика метода. Из названия следует, что главным объектом данного метода является площадь. Для ряда фигур, например для треугольника, площадь довольно просто выражается через разнообразные комбинации элементов фигуры (треугольника). Поэтому весьма эффективным оказывается прием, когда сравниваются различные выражения для площади данной фигуры. В этом случае возникает уравнение, содержащее известные и искомые элементы фигуры, разрешая которое мы определяем неизвестное. Здесь и проявляется основная особенность метода площадей – из геометрической задачи он «делает» алгебраическую, сводя все к решению уравнения (а иногда системы уравнений).
|
|
Само сравнение выражений для площади фигуры может быть различным. Иногда площадь фигуры представляется в виде суммы площадей ее частей. В других случаях приравниваются выражения, основанные на различных формулах площади для одной и той же фигуры, что позволяет получить зависимость между ее элементами.
Суть метода площадей не ограничивается только описанным выше приемом. Иногда бывает полезно рассмотреть отношение площадей фигур, одна из которых (или обе) содержит в себе искомые элементы.
В современных учебниках, пособиях и различного рода задачниках, к сожалению, уделяется мало внимания психологическим факторам, влияющим на успешность обучения математике. А именно, воспитание у учащихся уверенности в своих силах, развитие умения пользоваться прошлым опытом. В данном реферате предлагается разработка системы математических задач, решаемых методом площадей.
Реферат построен следующим образом. Берутся два общеизвестных утверждения, которые являются базовыми. На основе этих утверждений выстраиваются две «цепочки» задач по нарастающему уровню сложности. Решения задач в этих «цепочках» основаны на базовых утверждениях и на решении предыдущих задач.
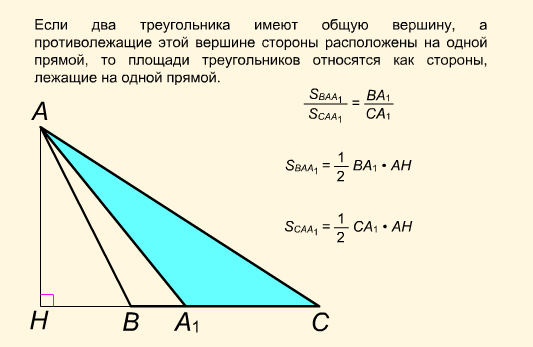
Утверждение 1. Два треугольника являются равновеликими, если равны их высоты и основания.
| Задача 1. Докажите, что диагональ параллелограмма делит его на два равновеликих треугольника. | 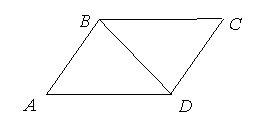
| Решение. Высоты треугольников ABD и BCD равны. AD = BC (по свойству параллелограмма). Тогда в силу утверждения 1 S▲ABD = S▲BCD |
| Задача 2. На стороне CD параллелограмма ABCD взята произвольная точка Е. Зная, что S▲ABE = S, найдите площадь параллелограмма ABCD. | 
| Решение. Проведем дополнительное построение: КЕ?AD. Тогда из задачи 1 следует, что S▲KBE= S▲CBE, а S▲AKE = S▲ADE . Отсюда SABCD = 2S |
| Задача 3. В параллелограмме ABCD на сторонах AB и CD взяты произвольные точки M и N. Докажите, что площадь четырехугольника KMEN равна площади четырех образовавшихся треугольников. | 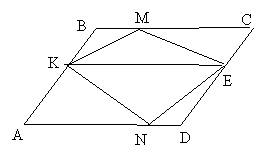
| Решение. Проведем отрезок КЕ. Тогда в силу задачи 2 S▲KME = S▲KMB + S▲MEC, а S▲KNE = S▲AKN + S▲EDN Отсюда S▲KMEN = S▲KMB + S▲MEC + S▲KNE + S▲EDN |
| Задача 4. Внутри параллелограмма ABCD взята произвольная точка О. Зная площадь трех треугольников с вершиной в точке О, найдите площадь четвертого треугольника. | 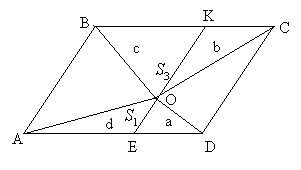
| Решение. Пусть S▲ADO = S1, S▲ABO = S2, S▲BOC = S3. Произведем дополнительное построение: КЕ?АВ. Введем следующие обозначения: S▲EOD = a, S▲KCO = b, S▲BKO = c, S▲AEO = d. Тогда S2 = с +d , S▲DOC = a + b, S1 + S3 = a + b + c + d . Отсюда S▲DCO = S1 + S3 - S2 |
| Задача 5.Каждая диагональ четырехугольника делит его на треугольники одинаковой площади. Докажите, что это параллелограмм. | 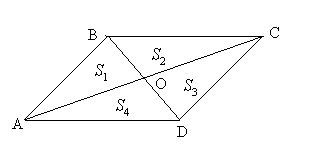
| Решение. Из условия следует, что верны равенства: S1 + S2 = S3 + S4 и S1 + S4 = S3 + S2 . Откуда получим, что S1 = S3, а S2 = S4. Отметим, что S2S1=AOOC, S4S3=AOOC. Кроме этого, соответствующие высоты треугольников BOC, COD и AOB, AOD равны, соответственно, площади относятся как длины оснований. Из того, что S1 = S3 и S2 = S4. следует, что AOOC=AOOC. Следовательно, AO = OC . Аналогично можно доказать, что BO = OD . Можно сделать вывод, что диагонали четырехугольника точкой пересечения делятся пополам, а это значит, что ABCD - параллелограмм. |
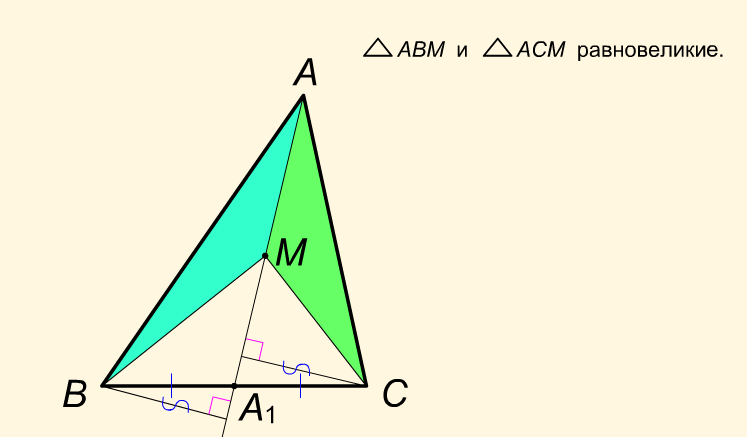
Утверждение 2. Медиана треугольника делит его на два равновеликих треугольника.
| Задача 6. В параллелограмме ABCD точка К – середина АВ, а L – середина ВС. Зная, что SKBLD = S , найдите SABCD . | 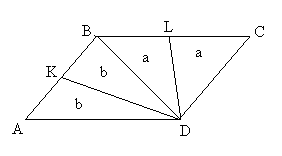
| Решение. Проведем диагональ ВD. Тогда, исходя из утверждения 2, получим, что SABCD = S. |
| Задача 7. В четырехугольнике ABCD точка Е, середина АВ, соединена с вершиной D, а точка F, середина CD, - с вершиной В. Докажите, что SABCD = 2SEBFD | 
| Решение. Проведя диагональ ВD и рассуждая аналогично задаче 6, получим, что SABCD = 2SEBFD |
| Задача 8. В произвольном четырехугольнике проведены отрезки, соединяющие середины сторон этого многоугольника. Зная площади трех из полученных четырехугольников, найдите площадь четвертого. | 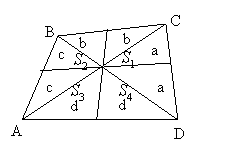
| Решение. В силу утверждения 2 и обозначений, использованных для элементов чертежа, получим S1 = a + b, S2 = b + c, S3 = c + d, S4 = a + d. Тогда, зная S1, S2, S3, S4 получим, что S4 = S1 + S3 - S2 . |
| Задача 9. Докажите, что диагонали параллелограмма делят его на четыре равновеликих треугольника. | 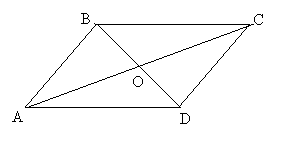
| Решение. В силу задачи 1 и утверждения 2 будем иметь S▲AOB = S▲BOC = S▲COD =S▲DOA |
| Задача 10. Середины двух параллельных сторон параллелограмма соединены с противолежащими вершинами. Какая часть площади параллелограмма ограничена проведенными отрезками? | 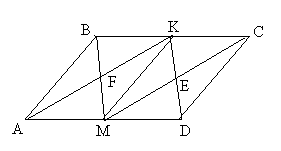
| Решение. Проведем отрезок МК. Тогда в силу задачи 9 SMFKE = 41SABCD. |
| Задача 12. На продолжениях сторон выпуклого четырехугольника АВСD отложены отрезки BB1 = AB, CC1 = BC, DD1 = CD и AA1 = AD. Докажите, что площадь четырехугольника А1В1С1D1 в 5 раз больше площади четырехугольника АВСD. | 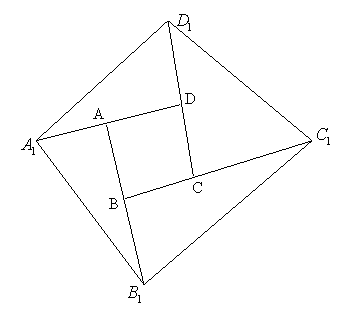
| Решение. Медиана делит площадь треугольника пополам, поэтому площади треугольников ABC, BB1C и CC1B1 равны между собой. Площадь треугольника ACD равна площади треугольника ADD1, площадь треугольника ADD1 равна площади треугольника AA1D1 и т. д. Тогда S▲BB1C1 = 2S▲ABC, S▲CC1D1 = 2S▲BCD, S▲AA1B1 = 2S▲DBA, S▲DD1A1 = 2S▲CAD. Суммируя эти равенства, получим S▲BB1C1 + S▲CC1D1 + S▲AA1B1 + S▲DD1A1.Обозначим площадь четырехугольника АВСD через S, тогда площадь четырех построенных треугольников равна 4S, а площадь четырехугольника А1В1С1D1 равна 5S. |
| Задача 13. Вершина А квадрата АВСD соединена с точкой О – серединой ВС, вершина В – с точкой Е – серединой СD, вершина С – с точкой N – серединой АD, а вершина D – с точкой К – серединой АВ. Точки пересечения проведенных прямых L, M, R, и Р служат вершинами четырехугольника LMRP. Докажите, что SLMRP=51SABCD. | 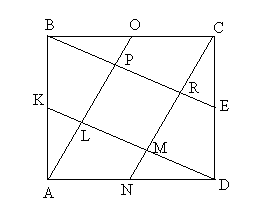 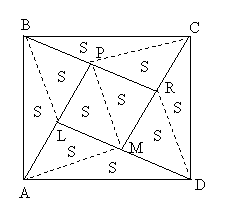
| Решение. ВКDE – параллелограмм, так как ВК = DE и ВК?DE, поэтому ВЕ?КD. АОСN – параллелограмм, так как АN = ОС и АN?ОС, поэтому ОА?СN. Учитывая, что О, Е, N, и К – середины сторон, из теоремы Фалеса следует, что АL = LP, BP = PR, CR = RM и DM = ML. Для большей наглядности дальнейшего хода решения задачи, представим чертеж в другом виде. Дальнейший ход решения совпадает с решением задачи 12. Продолжим «цепочку» задач, исходной фигурой в которых будет выступать уже треугольник. |
| Задача 14. На продолжении стороны АВ треугольника АВС взята точка К так, что АВ = ВК. Точка L – середина ВС. Зная, что S▲BKL = S, найдите S▲ABC. | 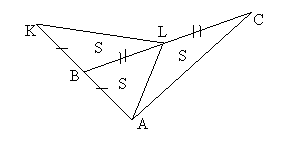
| Решение. Сделаем дополнительное построение – проведем отрезок AL. В силу утверждения 2 и использованных на чертежах обозначений S▲ABC = 2S . |
| Задача 15. На продолжении сторон треугольника АВС построены отрезки AA1 =AC, BB1 = AB и CC1 = BC . Докажите, что S▲A1B1C1 = 7S▲ABC. | 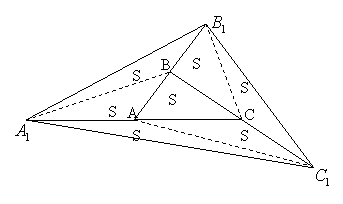
| Решение. Произведя дополнительные построения, приняв во внимание обозначения на чертеже и опираясь на утверждение 2, видим, что решение следует непосредственно из чертежа. |
Дата добавления: 2018-05-13; просмотров: 2052; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

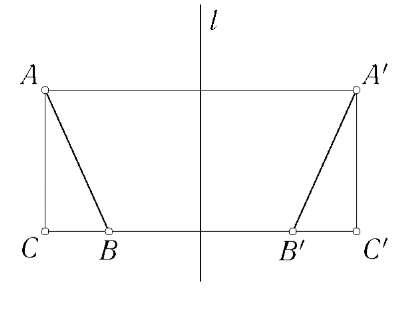 Рис. 6
Рис. 6