Задачи для самостоятельного решения.

Задача 3.1

Известно, что из числа зрителей определенной телепрограммы 70% смотрят и рекламные блоки. Группы состоящие из трех наугад выбранных телезрителей, опрашивают относительно содержания рекламного блока. Сколько человек в группе вероятнее всего смотрят рекламный блок?

Задача 3.2

Среди 12 проверяющих ревизором договоров семь оформлены неправильно. Найти вероятность того, что среди пяти договоров, произвольно отобранных ревизоров, окажутся неправильно оформленными не менее трех договоров.

Задача 3.3

Банк имеет пять отделений. Ежедневно с вероятностью 0,3 каждое отделение, независимо от других, может заказать на следующий день крупную сумму. В конце рабочего дня один из вице-президентов банка знакомиться с поступившими заявками. Найти вероятность того, что поступили заявки из двух отделений.

Задача 3.4

Владельцы кредитных карт ценят их и теряют весьма редко - вероятность потерять карту в течении недели для для случайно выбранного вкладчика равна 0,001 . Банк выдал кредитные карты 2000 клиентам. Найти вероятность того, что за неделю будет утеряна хотя бы одна кредитная карта.

Задача 3.5

Один процент сто долларовых купюр составляют фальшивые, сделанные настолько искусно, что операционист обменного пункта десятую их часть принимает за настоящие. Каждый день для обмена приносят примерно 200 стодолларовых купюр (всего- настоящих и фальшивых). Определить вероятность того, что среди них есть хотя бы одна фальшивая.

Задача 3.6

Строительная фирма для привлечения инвестиций для строительства нового дома собирается воспользоваться банковским кредитом. Вероятность того, что какой-либо банк в ответ на поступление бизнес-плана примет положительное решение о кредитовании фирмы, равна 0,3. Строительная фирма обратилась в 100 банков. Найти вероятность того, что решение о предоставлении кредитов этой фирме примут 15 банков.

Задача 3.7

Вероятность смерти тридцатилетнего мужчины составляет 0,0006. Страховая компания заключила 10 000 страховых контрактов с мужчинами в возрасте 30 лет, согласно которым в случае смерти застрахованного лица в течении ближайшего года его наследникам выплавится 100 тыс. руб . Стоимость одного контракта равна 1 200 руб. Найти вероятность того, что к концу года страховая компания окажется в убытке.

Задача 3.8

В страховом обществе на год застраховано 4000 автолюбителей. В случае аварии страховое общество выплачивает автолюбителю 800 рублей. Какую минимальную стоимость страхового взноса следует установить, чтобы вероятность того, что страховое общество к концу года окажется в убытке была не больше 0,0668, если вероятность автолюбителю попасть в аварию равна 0,004 .

Задача 3.8

Вероятность смерти тридцатилетнего мужчины составляет 0,0006. Страховая компания заключила 10 000 страховых контрактов с мужчинами в возрасте 30 лет, согласно которым в случае смерти застрахованного лица в течении ближайшего года его наследникам выплавится 100 тыс. руб . Стоимость одного контракта равна 1 200 руб. Найти вероятность того, что доход страховой компании превысит 4 000 000 рублей.

Задача 3.9

Численность работников предприятия составляет 500 чел. Вероятность невыхода на работу из-за болезни равна 0,01 для каждого работника предприятия. Определить вероятность того, что в ближайший день не выйдет на работу хотя бы один из работников.

Задача 3.10

Вероятность того, что человек в период страхования будет травмирован, равна 0,006. Компанией застраховано 100 человек. Годовой взнос с человека составляет 150 руб. В случае получения травмы застраховавшийся получает 12 000 руб. Какова вероятность того, что выплата по страховкам превысит сумму страховых взносов?

Задача 3.11

Торговый агент в среднем контактирует с восемью потенциальными покупателями в день. Из опыта ему известно, что вероятность того, что потенциальный покупатель совершит покупку, равна 0,1. Чему равна вероятность того, что у агента будут хотя бы две продажи в течение дня?

Задача 3.12

Фирма предлагает в продажу со склада партию из 10 компьютеров, 4 из которых – с дефектами. Покупатель приобретает 5 из них, не зная о возможных дефектах. Чему равна вероятность того, что все 5 компьютеров окажутся без дефектов?

Задача 3.13

Установлено, что виноградник поражен вредителями в среднем на 10%. Определить вероятность того, что из 10 проверенных кустов винограда один будет поражен.

Задача 3.14

Известно, что 80% специалистов в районе имеет высшее образование. Найти вероятность того, что из 100 наудачу отобранных человек высшее образование имеет не менее 70 чел.

Задача 3.15

В автопарке имеется 400 автомобилей. Вероятность безотказной работы каждого из них равна 0,9. С вероятность 0,95 определить границы, в которых будет находиться доля безотказно работавших машин в определенный момент времени.

Задача 3.16

Товаровед осматривает 24 образца товаров. Вероятность того, что каждый из образцов будет признан годным к продаже, равна 0,6. Найти наивероятнейшее число образцов, которые товаровед признает годными к продаже.

Задача 3.17

Для определения степени поражения винограда вредителями было обследовано 400 кустов. Вероятность поражения куста виноградника равна 0,03. Определить границы, в которых с вероятностью 0,9545 будет заключено число кустов, не пораженных вредителями.

Задача 3.18

Численность работников предприятия составляет 500 человек. Вероятность невыхода на работу из-за болезни равна 0,03 для каждого работника предприятия. Определить вероятность того, что в ближайший день не выйдет на работу хотя бы один работник.

Задача 3.19

Торговый агент в среднем контактирует с восемью потенциальными покупателями в день. Из опыта ему известно, что вероятность того, что потенциальный покупатель совершит покупку, равна 0,1. Чему равна вероятность того, что у агента в течении дня не будет продаж?

Задача 3.20

Дискретные случайные величины

Величина 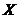называется дискретной случайной величиной, если ее возможные значения образуют конечную или бесконечную последовательность чисел , появление каждого из них есть случайное событие с определенной вероятностью.

Законом распределения дискретной случайной величины называется перечень ее возможных значений и соответствующих им вероятностей.

Пусть 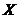-дискретная случайная величина, которая принимает значения: с некоторой вероятностью , где .

Тогда можно говорить о вероятности того, что случайная величина 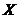приняла значение : .

Значения и соответствующие представляют в виде таблицы:

				…		…
				…		…

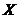
Основное свойство таблицы заключено в том, что сумма вероятностей равна 1:

Графическое изображение ряда распределения называется многоугольником распределении.

Наиболее общей формой закона распределения является функция распределения, представляющая собой вероятность того, что случайная величина 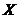примет значение меньше, чем заданное :

Свойства функции распределения:

1.

2. 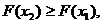если

3. ,

Для дискретной случайной величины 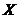функция распределения - разрывная ступенчатая функция, непрерывная слева (рис.2).

Вероятность того, что случайной величины 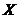примет значение, заключенное в интервале определяется по формуле:

Числовые характеристики дискретной случайной величины :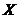

Математическое ожидание: .

Дисперсия: .

Среднее квадратическое отклонение:

Дата добавления: 2018-05-13; просмотров: 1154; Мы поможем в написании вашей работы!
Поделиться с друзьями:

⇐ Предыдущая 1 234 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!