Задачи для самостоятельного решения.

Стр 1 из 10Следующая ⇒

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение высшего профессионального образования

«ИЖЕВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Кафедра «Высшая математика»

Т.Н. Голубкова

Методические указания и задания

Для самостоятельной работы

по теории вероятностей и математической статистике

для студентов экономических специальностей ИжГТУ

Ижевск, 2010 г.

Оглавление

Предисловие………………………………………………………………………………………3

Основные теоремы теории вероятностей…………………………………………… 4
Формула полной вероятности. Формула Байеса…………………………………12.
Повторные испытания……………………………………………………………………………20
Дискретные случайные величины…………………………………………………………27
Непрерывные случайные величины………………………………………………………37
Анализ вариационных рядов…………………………………………………………………44
Статистические оценки параметров распределения (интервальные)…51
Статистическая проверка статистических гипотез…………………………………60

Приложения…………………………………………………………………………………………………68

Предисловие.

Предлагаемое учебное пособие предназначено для студентов специальности «Маркетинг в экономике», изучающих курс теории вероятностей и математической статистики.

В пособии представлены задачи для самостоятельного решения, которые служат для усвоения ключевых разделов теории вероятностей и математической статистики. В связи с большой ролью вероятностно-статистических методов в экономике, задачи составлены таким образом, чтобы дать студенту некоторые практические навыки по использованию статистических методов обработки и анализа эмпирических данных. В задачах рассматриваются ситуации, возникающие в практике управления экономическими и финансовыми системами. Экономические приложения методов теории вероятностей и математической статистики выходят на первый план, акцент делается не только на усвоение алгоритма решения задач, но и на анализ и экономическую интерпретацию полученных результатов.

В методических указаниях рассмотрены некоторые основные сведения из теории, приведены примеры решения типовых задач, а также ряд формул, необходимых для понимания изучаемого материала и решения задач.

Перед тем как приступить к разбору решений типовых задач, изложенных в данной методической разработке, студентам рекомендуется изучить теоретический материал в соответствии с программой.

Основные теоремы теории вероятностей.

Теорема 1.

Вероятность суммы двух несовместных событий и равна сумме их вероятностей:

Следствие 1. Если 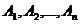- попарно несовместные события, то вероятность их суммы равна сумме вероятностей этих событий:

Следствие 2.Вероятность суммы попарно несовместных событий 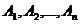, образующих полную группу, равна 1:

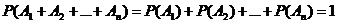
Следствие 3.События и несовместны и образуют полную группу событий, поэтому

Теорема 2.

Вероятность суммы двух совместных событий и равна сумме вероятностей этих событий без вероятности их произведения:

Теорема 3.

Вероятность произведения двух независимых событий и равна произведению их вероятностей:

Следствие.Вероятность произведения 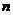независимых событий 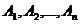равна произведению их вероятностей:

Условной вероятностью события , при условии, что событие уже произошло, называется число 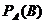, определяемое по формуле: .

Аналогично находится условная вероятность события , при условии, что событие уже произошло.

Теорема 4.

Вероятность произведения двух зависимых событий и равна произведению вероятности наступления события на условную вероятность события при условии, что событие уже произошло:

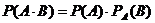
Следствие.Если события и независимы, то из теоремы 4 следует теорема 3.

Теорема 5.Вероятность произведения 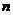зависимых событий 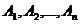равна произведению последовательно условных вероятностей:

Теорема 6.

Вероятность наступления хотя бы одного из зависимых событий 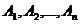равна разности между единицей и вероятностью произведения отрицаний событий :

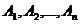Следствие 1.Вероятность наступления хотя бы одного из событий 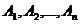- независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий:

Следствие 2.Если события имеют одинаковую вероятность появления, т.е. ,то вероятность появления хотя бы одного из них равна:

Примеры решения задач.

Задача 1

Покупатель может приобрести акции трех компаний: А , В и С . Надежность первой оценивается экспертами на уровне 90 %, второй – 83 % и третьей – 86 %. Чему равна вероятность того, что а) только одна компания в течение года станет банкротом; б) две компании обанкротятся; в) наступит хотя бы одно банкротство?

Решение

Рассмотрим события :

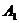= { первая компания окажется банкротом},

={вторая компания окажется банкротом}

={ третья компания окажется банкротом}.

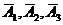- противоположные события, т.е. соответствующая компания не обанкротится.

а) Обозначим событие, состоящее в том, что только одна компания в течение года станет банкротом :

По условию : . Тогда:

; ;

Так как события независимые, а события , , несовместные, то, применяя теорему сложения для несовместных событий и теорему умножения для независимых событий, получим :

б) Событие {две компании обанкротятся }

в) Событие {наступит хотя бы одно банкротство}.

Событие {не будет ни одного банкрота}.

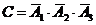
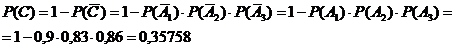
Ответ: а) 0,30754 ; б) 0,04766 ; в) 0,35758 .

Задача 2.

В урне 10 шаров, из которых два белые, а остальные черные. Наудачу друг за другом взято 2 шара. Найдите вероятность того, что оба шара черные.

Решение:

Рассмотрим элементарные события :

{оба шара черные}; {первый шар черный}; {второй шар черный};

Тогда: .

Вероятность того, что второй шар черный, будет зависеть от того, какого цвета первый шар. Если первый шар черный, то вероятность того, что второй шар также черного цвета, равна условной вероятности 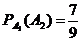, так как после наступления события 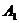всего останется 9 шаров ,из них 7 черных. Значит,

Ответ: .

Задачи для самостоятельного решения.

Задача 1.1

Консультационная фирма получила приглашение для выполнения двух работ от двух международных корпораций. Руководство фирмы оценивает вероятность получения заказа от фирмы А (событие А) равной 0,45. Также, по мнению руководителей фирмы в случае, если фирма заключит договор с компанией А, то с вероятностью в 90% компания В даст фирме консультационную работу. С какой вероятностью компания получит оба заказа?

Задача 1.2

Модельер, разрабатывающий новую коллекцию одежды к весеннему сезону, создает модели в зеленой, черной и красной цветовой гамме. Вероятность того, что зеленый цвет будет в моде весной, модельер оценивает в 0,3, что черный — в 0,2, а вероятность того, что будет моден красный цвет — в 0,15. Предполагая, что цвета выбираются независимо друг от друга, оцените вероятность того, что цветовое решение коллекции будет удачным хотя бы по одному из выбранных цветов.

Задача 1.3

Вероятность того, что потребитель увидит рекламу определенного продукта по каждому из 3 центральных телевизионных каналов, равна0,05. Предполагается, что эти события — независимы в совокупности. Чему равна вероятность того, что потребитель увидит рекламу: а) по всем 3 каналам; б) хотя бы по 1 из этих каналов?

Задача 1.4

Торговый агент предлагает клиентам иллюстрированную книгу. Из предыдущего опыта ему известно, что в среднем 1 из 65 клиентов, которым он предлагает книгу, покупает ее. В течение некоторого промежутка времени он предложил книгу 20 клиентам. Чему равна вероятность того, что он продаст им хотя бы 1 книгу? Прокомментируйте предположения, которые вы использовали при решении задачи.

Задача 1.5

В налоговом управлении работает 120 сотрудников, занимающих различные должности.

Все сотрудники	Руководители	Рядовые сотрудники	Итого
Мужчины	29	67	96
Женщины	4	20	24
Итого	33	87	120

На профсоюзном собрании женщины заявили о дискриминации при выдвижении на руководящие должности. Правы ли они?

Задача 1.6

В фирме 550 работников, 380 из них имеют высшее образование, а 412 — среднее специальное образование, у 357 высшее и среднее специальное образование. Чему равна вероятность того, что случайно выбранный работник имеет или среднее специальное, или высшее образование, или и то и другое?

Задача 1.7

Финансовый аналитик предполагает, что если норма (ставка) процента упадет за определенный период, то вероятность того, что рынок акций будет расти в это же время, равна 0,80. Аналитик также считает, что норма процента может упасть за этот же период с вероятностью 0,40. Используя полученную информацию, определите вероятность того, что рынок акций будет расти, а норма процента падать в течение обсуждаемого периода.

Задача 1.8

Вероятность для компании, занимающейся строительством терминалов для аэропортов, получить контракт в стране А равна 0,4, вероятность выиграть его в стране В равна 0,3. Вероятность того, что контракты будут заключены и в стране А, и в стране В, равна 0,12. Чему равна вероятность того, что компания получит контракт хотя бы в одной стране?

Задача 1.9

Город имеет 3 независимых резервных источника электроэнергии для использования в случае аварийного отключения постоянного источника электроэнергии. Вероятность того, что любой из 3 резервных источников будет доступен при отключении постоянного источника, составляет 0,8. Какова вероятность того, что не произойдет аварийное отключение электроэнергии, если выйдет из строя постоянный источник?

Задача 1.10

Покупатель может приобрести акции 2 компаний А и В. Надежность 1-й оценивается экспертами на уровне 90%, а 2-й - 80%. Чему равна вероятность того, что: а) обе компании в течение года не станут банкротами; б) наступит хотя бы одно банкротство?

Задача 1.11

Стандарт заполнения счетов, установленный фирмой, предполагает, что не более 5% счетов будут заполняться с ошибками. Время от времени компания проводит случайную выборку счетов для проверки правильности их заполнения. Исходя из того, что допустимый уровень ошибок - 5% и 10 счетов отобраны в случайном порядке, чему равна вероятность того, что среди них нет ошибок?

Задача 1.12

На сахарном заводе один из цехов производит рафинад. Контроль качества обнаружил, что 1 из 100 кусочков сахара разбит. Если вы случайным образом извлекаете 2 кусочка сахара, чему равна вероятность того, что, по крайней мере, 1 из них будет разбит? Предполагаем независимость событий, это предположение справедливо вследствие случайности отбора.

Задача 1.13

Эксперты торговой компании полагают, что покупатели, обладающие пластиковой карточкой этой компании, дающей право на скидку, с 90%-й вероятностью обратятся за покупкой определенного ассортимента товаров в ее магазины. Если это произойдет, обладатель пластиковой карточки приобретет необходимый ему товар в магазинах этой компании с вероятностью 0,8. Какова вероятность того, что из двух обладателей пластиковой карточки торговой компании только один приобретет необходимый ему товар в ее магазинах?

Задача 1.14

Аудиторская фирма размещает рекламу в журнале «Коммерсант». По оценкам фирмы 60% людей, читающих журнал, являются потенциальными клиентами фирмы. Выборочный опрос читателей журнала показал также, что 85% людей, которые читают журнал, помнят о рекламе фирмы, помещенной в конце журнала. Оцените, чему равен процент людей, которые являются потенциальными клиентами фирмы и могут вспомнить ее рекламу?

Задача 1.15

В городе 3 коммерческих банка, оценка надежности которых - 0,95, 0,90 и 0,85 соответственно. В связи с определением хозяйственных перспектив развития города администрацию интересуют ответы на следующие вопросы: а) какова вероятность того, что в течение года обанкротятся все 3 банка; б) что обанкротится хотя бы 1 банк?

Задача 1.16

О двух акциях А и В известно, что они выпущены одной и той же отраслью. Вероятность того, что акция А поднимется завтра в цене, равна 0,2. Вероятность того, что обе акции А и В поднимутся завтра в цене, равна 0,12. Предположим, что вы знаете, что акция А поднимется в цене завтра. Чему равна вероятность того, что и акция В завтра поднимется в цене?

Задача 1.17

Инвестор предполагает, что в следующем периоде вероятность роста цены акций компании Nбудет составлять 0,7, а компании М - 0,4. Вероятность того, что цены поднимутся на те и другие акции, равна 0,28. Вычислите вероятность их роста или компании N, или компании М, или обеих компаний вместе.

Задача 1.18

Крупная торговая компания занимается оптовой продажей материалов для строительства и ремонта жилья и, имея список покупателей в 3 регионах, основанный на ее собственной системе кодов, рассылает им по почте каталог товаров. Менеджер компании полагает, что вероятность того, что компания не получит откликов на разосланные предложения ни из одного региона, равна 0,25. Чему в этом случае равна вероятность того, что компания получит ответ хотя бы из одного региона?

Задача 1.19

Вероятность получить высокие дивиденды по акциям на первом предприятии 0,2, на втором – 0,35, а на третьем -0,15. Определить вероятность того, что акционер, имеющий акции всех предприятий, получит высокие дивиденды: а) только на одном предприятии; б) хотя бы на одном предприятии

Задача 1.20

Вероятность того, что покупатель, собирающийся приобрести компьютер и пакет прикладных программ, приобретет только компьютер, равна 0,15, только пакет программ - 0,1. Вероятность того, что будет куплен и компьютер, и пакет программ, равна 0,05. Чему равна вероятность того, что будет куплен или компьютер, или пакет программ, или компьютер и пакет программ вместе?

2. Формула полной вероятности. Формула Байеса.

Пусть событие может наступить только одновременно с одним из попарно несовместных событий , которые образуют полную группу. Кроме того, события имеют ненулевые вероятности.

Для любого наблюдаемого в эксперименте события имеет место следующее равенство, называемое формулой полной вероятности:

или

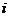где события - гипотезы, -условная вероятность наступления события при наступлении -й гипотезы ( , а безусловные вероятности трактуются как априорные (доопытные) вероятности гипотез.

Условная вероятность гипотезы , при условии того, что событие уже произошло, определяется по формуле вероятности гипотез или формуле Байеса:

где

Общая схема применения формулы Байеса следующая.

Пусть событие может происходить в различных условиях, о характере которых можно выдвинуть 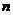гипотез . Из каких-то соображений

известны вероятности этих гипотез , , и известны условные вероятности .

Предположим, что произведен опыт, в результате которого наступило событие , тогда условные вероятности гипотез (их называют апостериорными или послеопытными) будут рассчитываться по формуле Байеса.

Примеры решения задач

Задача1 .

В составе Думы представлены 3 партии (по 100, 150, 50 человек от 1-й, 2-й и 3-й партий соответственно). Кандидата на должность спикера Думы поддерживают 50% представителей первой партии, 70% - второй партии и 10% - третьей партии. Какова вероятность того, что наудачу выбранный член Думы поддерживает выдвинутую кандидатуру на должность спикера Думы?

Решение:

Рассматривается событие A={наудачу выбранный представитель думы поддерживает выдвинутую кандидатуру}

Из условий задачи очевидно, что с событием тесно связаны три гипотезы:

{выбранное лицо представляет первую партию};

{выбранное лицо представляет вторую партию};

{выбранное лицо представляет третью партию}.

Вероятности этих гипотез сразу определяются из условии задачи:

; ;

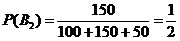Условные вероятности события даны в условии задачи:

; ;

Вероятность события вычисляем по формуле полной вероятности:

Ответ:0,7

Задача 2.

Страховая компания разделяет застрахованных по трем классам риска: 1 класс – малый риск, 2 класс – средний, 3 класс – большой риск. Среди всех клиентов компании 50% - первого класса риска, 30% - второго и 20% - третьего. Вероятность наступления страхового случая для первого класса риска равна 0.01, второго – 0.03, третьего – 0.08. Какова вероятность того, что клиент, получивший денежное вознаграждение за период страхования, относится к группе малого риска?

Решение.

Пусть событие А означает, что клиент компании получил вознаграждение. Понятно, что событие А может наступить лишь совместно с одним из трех попарно несовместных событий: - клиент относится к первому классу риска; - клиент относится ко второму классу риска; - клиент относится к третьему классу риска. Необходимо определить условную вероятность