Алгоритм проверки статистических гипотез.
- Располагая выборочными данными
 , формируют нулевую гипотезу
, формируют нулевую гипотезу  и конкурирующую
и конкурирующую  .
. - Задают уровень значимости
 (обычно принимают
(обычно принимают 


 ).
). - Рассматривается критерий
 :
:
· 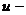 нормальное распределение;
нормальное распределение;
·  распределение Пирсона;
распределение Пирсона;
·  распределение Стьюдента;
распределение Стьюдента;
·  распределение Фишера-Снедокора.
распределение Фишера-Снедокора.
- На основании выборки
 определяют значение критерия
определяют значение критерия  (см. приложения 4-6)
(см. приложения 4-6)
Пример решения задачи
Задача.
Оценить существенность различий в средней урожайности двух сортов пшеницы, если для первого сорта средняя урожайность  ц/га и выборочная дисперсия
ц/га и выборочная дисперсия  , а для второго сорта средняя урожайность
, а для второго сорта средняя урожайность  и выборочная дисперсия
и выборочная дисперсия  . Объемы выборок
. Объемы выборок  и
и  соответственно. Считать, что совокупности распределены нормально и генеральные дисперсии известны (независимые выборки). Принять уровень значимости
соответственно. Считать, что совокупности распределены нормально и генеральные дисперсии известны (независимые выборки). Принять уровень значимости 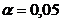 .
.
Решение:
Выдвигаем нулевую гипотезу о том, что средние урожайности двух сортов пшеницы не отличаются друг от друга, т.е.  , при альтернативной гипотезе
, при альтернативной гипотезе  - урожайности существенно различны.
- урожайности существенно различны.
Так как выборки независимы, причем  , то применим критерий
, то применим критерий 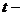 Стьюдента с
Стьюдента с  степенями свободы, где
степенями свободы, где  .
.
По приложению……

По приложению 4 определим критическое значение t- распределения для двусторонней области:  .
.
Так как  , то нулевую гипотезу следует отклонить. Следовательно, два сорта пшеницы отличаются значимо по величине урожайности.
, то нулевую гипотезу следует отклонить. Следовательно, два сорта пшеницы отличаются значимо по величине урожайности.
Задачи для самостоятельного решения.
|
|
|
Задача 8.1
Компания, производящая средства для потери веса, утверждает, что прием таблеток в сочетании со специальной диетой позволяет сбросить в среднем в неделю 400 г. Веса. Случайным образом отобраны 25 человек, использующих эту терапию, и обнаружено, что в среднем еженедельная потеря в весе составила 430 г. Со средним квадратическим отклонением 110 г. Проверьте гипотезу о том, что средняя потеря в весе составляет 400 г. Уровень значимости  .
.
Задача 8.2
Поступление страховых взносов в 130 филиалов страховых организаций в регионе А составило 26*104 у.е., в регионе В на 100 филиалов пришлось 18*104 у.е. Дисперсия величины страховых взносов в регионе А равна 39*108 (у. е.)2, в регионе В – 25*108 (у. е.)2. На уровне значимости  определите, существенно ли различается средняя величина поступления страховых взносов в регионах А и В из расчета на 1 филиал.
определите, существенно ли различается средняя величина поступления страховых взносов в регионах А и В из расчета на 1 филиал.
Задача 8.3
Компания утверждает, что новый вид зубной пасты для детей лучше предохраняет зубы от кариеса, чем зубные пасты, производимые другими фирмами. Для проверки эффекта в случайном порядке была отобрана группа из 400 детей, которые пользовались новым видом зубной пасты. Другая группа из 300 детей, также случайно выбранных, в это же время пользовалась другими видами зубной пасты. После окончания эксперимента было выяснено, что у 30 детей, использующих новую пасту, и 25 детей из контрольной группы появились новые признаки кариеса. Имеются ли у компании достаточные основания для утверждения о том, что новый сорт зубной пасты эффективнее предотвращает кариес, чем другие виды зубной пасты? Принять уровень значимости  .
.
|
|
|
Задача 8.4
В 1995 г. Число договоров добровольного страхования, заключенных государственными страховыми организациями, составило в Ростовской области 1858*103 на сумму 7461*106 руб. Негосударственные страховые организации заключили 1250*104 договоров добровольного страхования на сумму 34884*106 руб. Предположительно дисперсия страховой суммы договоров, заключенных государственными страховыми организациями, равна 1016 руб.2, а договоров, заключенных негосударственными страховыми организациями, - 8*1017 руб.2. Имеются ли существенные различия в средних размерах страховых сумм договоров добровольного страхования, заключаемых государственными и негосударственными страховыми организациями? Уровень значимости  принять равным 0,01.
принять равным 0,01.
Задача 8.5
|
|
|
Крупный коммерческий банк заказал маркетинговое исследование по выявлению эффекта «премирования» (калькулятор, набор ручек и др.) как стимула для открытия счета в банке. Для проверки случайным образом было отобрано 200 «премированных» посетителей и 200 «непремированных». В результате выяснилось, что 89% посетителей, которым предлагалась премия, и 79% посетителей, которым не предлагалась премия, открыли счет в банке в течение 6 мес. Используя эти данные, проверьте гипотезу о том, что доля «премированных» посетителей, открывших счет в банке, статистически существенно отличается от удельного веса «непремированных» посетителей, открывших счет в банке. Принять уровень значимости  .
.
Задача 8.6
Инженер по контролю качества проверяет среднее время горения нового вида электроламп. Для проверки в порядке случайной выборки было отобрано 100 ламп, среднее время горения которых составило 1075 ч. Предположим, что среднее квадратическое отклонение времени горения для генеральной совокупности известно и составляет 100 ч. Используя уровень значимости  , проверьте гипотезу о том, что среднее время горения ламп – более 1 000 ч.
, проверьте гипотезу о том, что среднее время горения ламп – более 1 000 ч.
Предположим, что инженер по контролю качества не имеет информации о генеральной дисперсии и использует выборочное среднее квадратическое отклонение. Изменится ли ответ задачи?
|
|
|
Задача 8.7
Компания, выпускающая в продажу новый сорт растворимого кофе, провела проверку вкусов покупателей по случайной выборке из 400 человек и выяснила, что 220 из них предпочли новый сорт всем остальным. Проверьте на уровне значимости  гипотезу о том, что, по крайней мере, 52% потребителей предпочтут новый сорт кофе.
гипотезу о том, что, по крайней мере, 52% потребителей предпочтут новый сорт кофе.
Задача 8.8
Страховая компания изучает вероятность дорожных происшествий для подростков, имеющих мотоциклы. За прошедший год проведена случайная выборка 2 000 страховых полисов подростков-мотоциклистов и выявлено, что 15 из них попадали в дорожные происшествия и предъявили компании требование о компенсации за ущерб. Может ли аналитик компании отклонить гипотезу о том, что менее 1% всех подростков-мотоциклистов, имеющих страховые полисы, попадали в дорожные происшествия в прошлом году? Принять уровень значимости  .
.
Задача 8.9
Новое лекарство, изобретенное для лечения атеросклероза, должно пройти экспериментальную, проверку для выяснения возможных побочных эффектов. В ходе эксперимента лекарство принимали 4 тыс. мужчин и 5 тыс. женщин. Результаты выявили, что 60 мужчин и 100 женщин испытывали побочные эффекты при приеме нового медикамента. Можем ли мы на основании эксперимента утверждать, что побочные эффекты нового лекарства у женщин проявляются в большей степени, чем у мужчин? Принять уровень значимости  .
.
Задача 8.10
В 1995 г. В Ростовской области обследовано 12 промышленных предприятий и 14 строительных (подрядных) организаций. Средняя балансовая прибыль промышленных предприятий оказалась равной 25*107pyб., а строительных организаций – 12*108 руб. Исправленная выборочная дисперсия прибыли промышленных предприятий составила 64*1016 руб.2, строительных организаций – 16*1016 руб.2. На уровне значимости  определите, являются ли различия в результатах финансовой деятельности промышленных предприятий и строительных организаций случайными.
определите, являются ли различия в результатах финансовой деятельности промышленных предприятий и строительных организаций случайными.
Задача 8.11
На 1 января 1996 г. Численность беженцев в Ростовской области составляла 32 412 чел. При общей численности наличного населения 4425400 чел. В Краснодарском крае на 5043900 чел. Наличного населения приходилось 30423 беженца. На уровне значимости  ответьте на вопрос: «Объясняется ли более высокий удельный вес беженцев в общей численности населения в Ростовской области в сравнении с Краснодарским краем случайными факторами или имеет смысл поиск факторов, обусловивших это явление?»
ответьте на вопрос: «Объясняется ли более высокий удельный вес беженцев в общей численности населения в Ростовской области в сравнении с Краснодарским краем случайными факторами или имеет смысл поиск факторов, обусловивших это явление?»
Задача 8.12
Компания по производству безалкогольных напитков предполагает выпустить на рынок новую модификацию популярного напитка, в котором сахар заменен сукразитом. Компания хотела бы быть уверенной в том, что не менее 70% ее потребителей предпочтут новую модификацию напитка. Новый напиток был предложен на пробу 2 тыс. чел., и 1422 из них сказали, что он вкуснее старого. Может ли компания отклонить предположение о том, что только 70% всех ее потребителей предпочтут новую модификацию напитка старой? Принять уровень значимости  .
.
Задача 8.13
Производители нового типа аспирина утверждают, что он снимает головную боль за 30 мин. Случайная выборка 100 чел., страдающих головными болями, показала, что новый тип аспирина снимает головную боль за 28,6 мин при среднем квадратическом отклонении 4,2 мин. Проверьте на уровне значимости  справедливость утверждения производителей аспирина о том, что это лекарство излечивает головную боль за 30 мин.
справедливость утверждения производителей аспирина о том, что это лекарство излечивает головную боль за 30 мин.
Задача 8.14
Доля убыточных предприятий в промышленности в целом по России в 1995 г. Составила 26%, а в Ростовской области – 27%. В 1995 г. В Ростовской области насчитывалось 7579 промышленных предприятий. На уровне значимости  определите, являются ли различия в удельном весе убыточных промышленных предприятий в России и в Ростовской области случайными или в Ростовской области действует комплекс экономических условий, обусловливающих повышенную долю нерентабельных предприятий?
определите, являются ли различия в удельном весе убыточных промышленных предприятий в России и в Ростовской области случайными или в Ростовской области действует комплекс экономических условий, обусловливающих повышенную долю нерентабельных предприятий?
Задача 8.15
В 1995 г. Доля предприятий государственной формы собственности в Ростовской области составила 2,3% от общего числа промышленных предприятий. Среди 2236 машиностроительных и металлообрабатывающих предприятий она оказалась равной 2,1%. На уровне значимости
 определите, существенно ли меньше удельный вес государственных предприятий в машиностроении и металлообработке, чем в целом в промышленности области?
определите, существенно ли меньше удельный вес государственных предприятий в машиностроении и металлообработке, чем в целом в промышленности области?
Задача 8.16
В 1996 г. Годовой оборот 4 бирж в регионе А составил 12*104 у.е.; в регионе В годовой оборот 5 бирж — 125*103 у. е. Исправленная выборочная дисперсия оборота в регионе А оказалась равной З*104(у.е.)2, в регионе В – 2*104 (у. е.)2. Можно ли на уровне значимости  утверждать, что средний оборот бирж в регионе А больше, чем в регионе В?
утверждать, что средний оборот бирж в регионе А больше, чем в регионе В?
Задача 8.17
Компания, занимающаяся консультированием в области инвестиций, заявляет, что среднегодовой процент по акциям определенной отрасли промышленности составляет 11,5%. Инвестор, желая проверить истинность этого утверждения, на основе случайной выборки 50 акций выявил, что среднегодовой процент по ним составил 10,8% с исправленным средним квадратическим отклонением  3,4%. На основе имеющейся информации определите, имеет ли инвестор достаточно оснований, чтобы опровергнуть заявление компании? Принять уровень значимости
3,4%. На основе имеющейся информации определите, имеет ли инвестор достаточно оснований, чтобы опровергнуть заявление компании? Принять уровень значимости  .
.
Задача 8.18
Производитель некоторого вида продукции утверждает, что 95% выпускаемой продукции не имеют дефектов. Случайная выборка 100 изделий показала, что только 92 из них свободны от дефектов. Проверьте справедливость утверждения производителя продукции на уровне значимости  .
.
Задача 8.19
Главный бухгалтер большой корпорации провел обследование по данным прошедшего года с целью выяснения доли некорректных счетов. Из 2000 выбранных счетов в 25 оказались некорректные проводки. Для уменьшения доли ошибок он внедрил новую систему. Год спустя он решил проверить, как работает новая система, и выбрал для проверки в порядке случайного отбора 3000 счетов компании. Среди них оказалось 30 некорректных. Можем ли мы утверждать, что новая система позволила уменьшить долю некорректных проводок в счетах? Принять уровень значимости  .
.
Задача 8.20
Владелец фирмы считает, что добиться более высоких финансовых результатов ему помешала неравномерность поставок комплектующих по месяцам года, несмотря на то, что поставщик в полном объеме выполнил свои обязательства за год. Поставщик утверждает, что поставки были не так уж неравномерны. Распределение поставок по месяцам года имеет следующий вид:
| Месяц | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Объем поставок, единиц | 19 | 23 | 26 | 18 | 20 | 20 | 20 | 20 | 32 | 27 | 35 | 40 |
На уровне значимости  определите, кто прав: владелец фирмы или поставщик? Изменится ли ответ на поставленный вопрос, если уровень значимости принять равным 0,01? Объясните результаты.
определите, кто прав: владелец фирмы или поставщик? Изменится ли ответ на поставленный вопрос, если уровень значимости принять равным 0,01? Объясните результаты.
Литература
1. Гмурман Г.Е.
Теория вероятностей и математическая статистика. Учебное пособие для вузов.-М.:Высшая школа,2003
2. Гмурман Г.Е.
Руководство к решению задач по теории вероятностей и математической статистике: Учебное пособие для студентов вузов. Изд.5-е, стер.-М.: Высшая шк.,2000.
3. Горелова Г.В., Кацко И.А.
Теория вероятностей и математическая статистика в примерах и задачах с применением Eхcel: Учебное пособие для вузов/Серия «Высшее образование».-Ростов н/Д: Феникс,2005.
4. Закс Л.
Статистическое оценивание. Пер. с нем. В.М.Варыгина. Под ред. Ю.Адлера, В.Г.Горского. М., «Статистика», 1976.
5. Кремер Н.Ш.
Теория вероятностей и математическая статистика: Учебное пособие для вузов.- М.: ЮНИТИ-ДАНА, 2000.
6. Пустыльнк Е.И.
Статистические методы анализа и обработки наблюдений. М.: Наука, 1968.
Приложения.
Приложение 1
Значения функций
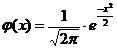 и
и 

| 
| 
| 
| 
| 
| 
| 
| 
|
| 0,00 01 02 03 04 05 06 07 08 09 0,10 11 12 13 14 15 16 17 18 19 0.20 21 22 23 24 25 26 27 28 29 | 0,3989 3989 3989 3988 3986 3984 3982 3980 3977 3973 0,3970 3964 3961 3956 3951 3945 3939 3932 3925 3918 0,3910 3902 3894 3885 3876 3867 3857 3847 3836 3825 | 0,000 0040 0080 0120 0160 0199 0239 0279 0319 0359 0,0398 0438 0478 0517 0557 0596 0636 0675 0714 0753 0,0793 0832 0871 0910 0948 0987 1026 1064 1103 1141 | 0,30 31 32 33 34 35 36 37 38 39 0,40 41 42 43 44 45 46 47 48 49 0.50 51 52 53 54 55 56 57 58 59 | 0,3814 3802 3790 3778 3765 3752 3739 3726 3712 3697 0.3683 3668 3652 3637 3621 3605 3589 3572 3555 3538 0,3521 3503 3485 3467 3448 3429 3410 3391 3372 3352 | 0,1179 1217 1255 1293 1331 1368 1406 1443 1480 1517 0,1554 1591 1628 1664 1700 1736 1772 1808 1844 1879 0,1915 1950 1985 2019 2054 2088 2123 2157 2190 2224 | 0,60 61 62 63 64 65 66 67 68 69 0,70 71 72 73 74 75 76 77 78 79 0,80 81 82 83 84 85 86 87 88 89 | 0,3332 3312 3292 3271 3251 3230 3209 3187 3166 3144 0,3123 3101 3079 3056 3034 3011 2989 2966 2943 2920 0,2897 2874 2850 2827 2803 2780 2756 2732 2709 2685 | 0,2257 2291 2324 2357 2389 2422 2454 2486 2517 2549 0,2580 2611 2642 2673 2703 2734 2764 2794 2823 2852 0,2881 2910 2939 2967 2995 3023 3051 3078 3106 3133 |
Продолжение приложения 1
.

| 
| 
| 
| 
| 
| 
| 
| 
|
| 0,90 91 92 93 94 95 96 97 98 99 1,00 01 02 03 04 05 06 07 08 09 1,10 11 12 13 14 15 16 17 18 19 1,20 21 22 23 24 25 26 27 | 0,2661 2637 2613 2589 2565 2541 2516 2492 2468 2444 0,2420 2396 2371 2347 2323 2299 2275 2251 2227 2203 0,2179 2155 2131 2107 2083 2059 2036 2012 1989 1965 0,1942 1919 1895 1872 1849 1826 1804 1781 | 0,3159 3186 3212 3238 3264 3289 3315 3340 3365 3389 0,3413 3438 3461 3485 3508 3531 3554 3577 3599 3621 0,3643 3665 3686 3708 3729 3749 3770 3790 3810 3830 0,3849 3869 3883 3907 3925 3944 3962 3980 | 28 29 1,30 31 32 33 34 35 36 37 38 39 1,40 41 42 43 44 45 46 47 48 49 1,50 51 52 53 54 55 56 57 58 59 1,60 61 62 63 64 65 | 1758 1736 0,1714 1691 1669 1647 1626 1604 1582 1561 1539 1518 0,1497 1476 1456 1435 1415 1394 1374 1354 1334 1315 0,1295 1276 1257 1238 1219 1200 1182 1163 1145 1127 0,1109 1092 1074 1057 1040 1023 | 3997 4015 0,4032 4049 4066 4082 4099 4115 4131 4147 4162 4177 0,4192 4207 4222 4236 4251 4265 4279 4292 4306 4319 0,4332 4345 4357 4370 4382 4394 4406 4418 4429 4441 0,4452 4463 4474 4484 4495 4505 | 66 67 68 69 1,70 71 72 73 74 75 76 77 78 79 1,80 81 82 83 84 85 86 87 88 89 1,90 91 92 93 94 95 96 97 98 99 2,00 02 04 06 | 1006 0989 0973 0957 0,0940 0925 0909 -893 0878 0863 0848 0833 0818 0804 0,0790 0775 0761 0748 0734 0721 0707 0694 0681 0669 0,0656 0644 0632 0620 0608 0596 0584 0573 0562 0551 0,0540 0,0519 0498 04788 | 4515 4525 4535 4545 0,4554 4564 4573 4582 4591 4599 4608 4616 4625 4633 0,4641 4649 4656 4664 4671 4678 4686 4693 4699 4706 0,4713 4719 4726 4732 4738 4744 4750 4756 4761 4767 0,4772 4783 4793 4803 |
Продолжение приложения 1

| 
| 
| 
| 
| 
| 
| 
| 
|
| 08 10 12 14 16 18 2,20 22 24 26 28 30 32 34 36 38 2,40 42 44 46 | 0459 0440 0422 0404 0387 0371 0,0355 0339 0325 0310 0297 0283 0270 0258 0246 0235 0,0224 0213 0203 0194 | 4812 4821 4830 4838 4846 4854 0,4861 4868 4875 4881 4887 4893 4898 4904 4909 4913 0,4918 4922 4927 4931 | 48 50 52 54 56 58 2,60 62 64 66 68 70 72 74 76 78 2,80 82 84 86 | 0184 0175 0167 0158 0151 0143 0,0136 0129 0122 0116 0110 0104 0099 0093 0088 0084 0,0079 0075 0071 0067 | 4934 4938 4941 4945 4948 4951 0,4953 4956 4959 4961 4963 4965 4967 4969 4971 4973 0,4974 4976 4977 4979 | 88 90 92 94 96 98 3,00 3,10 3,20 3,30 3,40 3,50 3,60 3,70 3,80 3,90 4,00 4,50 5,00 | 0063 0060 0056 0053 0050 0047 0,00443 00327 00238 00172 00123 00087 0061 00042 00029 00020 0,0001338 0000160 0000015 | 4980 4981 4982 4984 4985 4986 0,49865 49903 49931 49952 49966 49977 499841 49989 499928 49995 499968 499997 499999 |
Приложение 2
Таблица значений  .
.

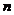
| 0,95 | 0,99 | 0,999 | 
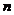
| 0,95 | 0,99 | 0,999 |
| 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | 2,78 2,57 2,45 2,37 2,31 2,26 2,23 2,20 2,18 2,16 2,15 2,13 2,12 2,11 2,10 | 4,60 4,03 3,71 3,50 3,36 3,25 3,17 3,11 3,06 3,01 2,98 2,95 2,92 2,90 2,88 | 8,61 6,86 5,96 5,41 5,04 4,78 4,59 4,44 4,32 4,22 4,14 4,07 4,02 3,97 3,92 | 20
25
30
35
40
45
50
60
70
80
90
100
120

| 2,093 2,064 2,045 2,032 2,023 2,016 2,009 2,001 1,996 1,991 1,987 1,984 1,980 1,960 | 2,861 2,797 2,756 2,720 2,708 2,692 2,679 2,662 2,649 2.640 2,633 2,627 2,617 2,576 | 3,883 3,745 3,659 3,600 3,558 3,527 3,502 3,464 3,439 3,418 3,403 3,392 3,374 3,291 |
Приложение 3
Таблица значений 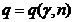 .
.

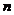
| 0,95 | 0,99 | 0,999 | 
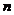
| 0,95 | 0,99 | 0,999 |
| 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | 1,37 1,09 0,92 0,80 0,71 0,65 0,59 0,55 0,52 0,48 0,46 0,44 0,42 0,40 0,39 | 2,67 2,01 1,62 1,38 1,20 1,08 0,98 0,90 0,83 0,78 0,73 0,70 0,66 0,63 0,60 | 5,64 3,88 2,98 2,42 2,06 1,80 1,60 1,45 1,33 1,23 1,15 1,07 1,01 0,96 0,92 | 20 25 30 35 40 45 50 60 70 80 90 100 150 200 250 | 0,37 0,32 0,28 0,26 0,24 0,22 0,21 0,188 0,174 0,161 0,151 0,143 0,115 0,099 0,089 | 0,58 0,49 0,43 0,38 0,35 0,32 0,30 0,269 0,245 0,226 0,211 0,198 0,160 0,136 0,120 | 0,88 0,73 0,63 0,56 0,50 0,46 0,43 0,38 0,34 0,31 0,29 0,27 0,211 0,185 0,162 |
Приложение 4
Критические точки t-распределения Стьюдента.
| Число степеней свободы | Уровень значимости | |||||||
| 0,10 | 0,05 | 0,02 | 0,01 | 0,002 | 0,001 | |||
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
40
60
120

| 6,31 2,92 2,35 2,13 2,01 1,94 1,90 1,86 1,83 1,81 1,80 1,78 1,77 1,76 1,75 1,75 1,74 1,73 1,73 1,73 1,72 1,72 1,71 1,71 1,71 1,71 1,70 1,70 1,70 1,70 1,68 1,67 1,66 1,65 | 12,71 4,30 3,18 2,78 2,57 2,45 2,37 2,31 2,26 2,23 2,20 2,18 2,16 2,15 2,13 2,12 2,11 2,10 2,09 2,09 2,08 2,07 2,07 2,06 2,06 2,06 2,05 2,05 2,05 2,04 2,02 2,00 1,98 1,96 | 31,82 6,97 4,54 3,75 3,37 3,14 3,00 2,90 2,82 2,76 2,72 2,68 2,65 2,62 2,60 2,58 2,57 2,55 2,54 2,53 2,52 2,51 2,50 2,49 2,49 2,48 2,47 2,47 2,46 2,46 2,42 2,39 2,36 2,33 | 63,66 9,93 5,84 4,60 4,03 3,71 3,50 3,36 3,25 3,17 3,11 3,06 3,01 2,98 2,95 2,92 2,90 2,88 2,86 2,85 2,83 2,82 2,81 2,80 2,79 2,78 2,77 2,76 2,76 2,75 2,70 2,66 2,62 2,58 | 318,31 22,33 10,22 7,17 5,89 5.21 4,79 4,50 4,30 4,14 4,03 3,93 3,85 3,79 3,73 3,69 3,65 3,61 3,58 3,55 3,53 3,51 3,49 3,47 3,45 3,44 3,42 3,41 3,40 3,39 3,31 3,23 3,16 3,09 | 636,62 31,60 12,92 8,61 6,87 5,96 5,41 5,04 4,78 4,59 4,44 4,32 4,22 4,14 4,07 4,02 3,97 3,92 3,88 3,85 3,82 3,79 3,77 3,75 3,73 3,71 3,69 3,67 3,66 3,65 3,55 3,46 3,37 3,29 | ||
|
| 0,05 | 0,025 | 0,01 | 0,005 | 0,001 | 0,0005 | ||
| Уровень значимости | ||||||||
Приложение 5
Сравнение дисперсий.
| Одна выборка | ||
|
| ||
| Дано: | ||
|
а) б)
| ||
| Двусторонний критерий | Односторонний критерий | |

| 
| 
|
| Если то
|  при
при 
|  при
при 
|
|
| ||
Продолжение приложения 5
| Две выборки | |
|
| |
| Дано: | |
|
| |
| Двусторонний критерий | Односторонний критерий |

| 
|
 , при , при  . .
|  при при  . .
|
|
| |
Приложение 6
Сравнение выборочной средней с генеральной средней (одна выборка): 
| Большой объем выборки (генеральная дисперсия известна | ||
|
| ||
| Двусторонний критерий | Односторонний критерий | |

| 
| 
|

| 
| 
|

|
| |
|
| ||
Продолжение приложения 6
| Малый объем выборки(генеральная дисперсия не известна) | ||
|
| ||
| Двусторонний критерий | Односторонний критерий | |

| 
| 
|

| 
| 
|
|
| ||
Приложение 7
Дата добавления: 2018-05-13; просмотров: 1675; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

 (
(  - генеральная дисперсия)
- генеральная дисперсия)


 при
при  - по таблице Пирсона.
- по таблице Пирсона. - при
- при 
 -по таблице распределения Лапласа.
-по таблице распределения Лапласа. ,
, при
при 
 при
при 



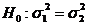


 , при
, при  ,
,  ,
, 
 - определяется по таблице распределения Фишера-Снедекора
- определяется по таблице распределения Фишера-Снедекора )
)

 -по таблице значений интеграла Лапласа,
-по таблице значений интеграла Лапласа, 

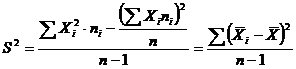
 - по таблице распределения Стьюдента
- по таблице распределения Стьюдента