Теорема сложения вероятностей.
Теория сложения вероятностей формируется следующим образом: вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:
P(A+B) = P(A)+P(B)
Теорема сложения вероятностей применима к любому числу несовместных событий. Ее удобно записать в виде: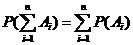 
Следствие 1. Если события А1, А2…, Аn образуют, полную группу несовместных событий, то сумма их вероятностей равна единице: 
Доказательство. Так как события А1, А2…, Аn образуют полную группу, то появление хотя бы одного из них — достоверное событие: P(A1+ A2 +…+An) = 1
P(A1+ A2 +…+An) = P(A1)+ P(A2)+…+ P(An) =
Противоположными событиями называются два несовместных события, образующих полную группу.
Следствие 2. Сумма вероятностей противоположных событий равна единице: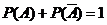 
Дифференциальное преобразование случайных функций.
Дана случайная функция X(t) с математическим ожиданием mx(t) и корреляционной функцией Кx(t, t'). Случайная функция Y(t) связана со случайной функцией X(t) линейным однородным оператором дифференцирования: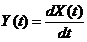 
Требуется найти my(t) и Кy(t, t’).
Представим производную в виде предела: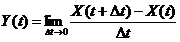 
è my(t) = M[Y(t)] = 
т. е. математическое ожидание производной от случайной функции равно производной от ее математического ожидания.
Для определения Ky(t, t’) перейдем к центрированным случайным функциям Y(t) и X(t); очевидно,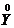 
(t)= 
По определению Ky(t, t’) = M[ 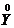(t) 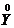(t’)] = M[ 
] = 
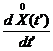è Ky(t, t’) = 
|
|
|
Итак, чтобы найти корреляционную функцию производной, нужно дважды продифференцировать корреляционную функцию исходной случайной функции: сначала по одному аргументу, затем — по другому.
Если случайная функция X(t) с математическим ожиданием mx(t) и корреляционной функцией Kx(t, t') преобразуется линейным однородным оператором L в случайную функцию
Y(t) = L{X(t)};
то для нахождения математического ожидания случайной функции Y(t) нужно применить тот же оператор к математическому ожиданию случайной функции X(t):
my(t) = L{mx(t)}
а для нахождения корреляционной функции нужно дважды применить тот же оператор к корреляционной функции случайной функции X(t), сначала по одному аргументу, затем — по другому: Ky(t, t’) = L(t)L(t'){Kx(t, t’)}
Дисперсию Dy (t) можно найти, зная корреляционную функцию:
Dy (t) = Ky(t, t).
Задача 4.16
Для получения небрака:
+) В первой технологии: 
+) Во второй технологии: 
Но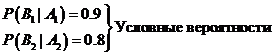 
Экзаменационный Билет №31
Случайная величина. Функция и плотность распределения вероятностей для случайных величин.
Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, причем неизвестно заранее, какое именно.
|
|
|
Такие случайные величины, принимающие только отделенные друг от друга значения, которые можно заранее перечислить, называются прерывными или дискретными случайными величинами.
Такие случайные величины, возможные значения которых непрерывно заполняют некоторый промежуток, называются непрерывными случайными величинами.
Сумма вероятностей всех возможных значений случайной величины равна единице. Эта суммарная вероятность каким-то образом распределена между отдельными значениями.
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Простейшей формой задания этого закона является таблица, в которой перечислены возможные значения случайной величины и соответствующие им вероятности:
Такую таблицу мы будем называть рядом распределения случайной величины X.
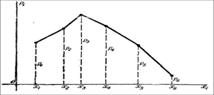
Многоугольник распределения
Функция распределения — самая универсальная характеристика случайной величины. Она существует для всех случайных величин: как прерывных, так и непрерывных.
Эта функция обозначается F(x): F(x)=P(X<x).
Некоторые общие свойства функции распределения.
|
|
|
v Функция распределения F(x) есть неубывающая функция своего аргумента, т. е. при.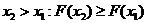 
v На минус бесконечности функция распределения равна нулю: F (-∞) = 0.
v На плюс бесконечности функция распределения равна единице: F (∞) = 0.
График функции распределения F (х) в общем случае представляет собой график неубывающей функции (рис. 5.2.2), значения которой начинаются от 0 и доходят до 1, причем в отдельных точках функция может иметь скачки (разрывы).
Действительно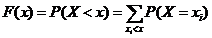 
Плотность распределения:
Пусть имеется непрерывная случайная величина X с функцией распределения F(x), которую мы предположим непрерывной и дифференцируемой. Вычислим вероятность попадания этой случайной величины на участок от х до х+Δх:
Р (х < X < х + Δx) = F (х + Δх) — F (х).
Рассмотрим среднюю вероятность, приходящуюся на единицу длины на этом участке, и будем приближать Δx к нулю. В пределе получим производную от функции распределения:
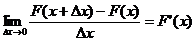
Функция f(х)=F’(x) - производная функции распределения - называется плотностью распределения непрерывной случайной величины X. Она существует только для непрерывных случайных величин.
Иногда функцию f(x) называют также «дифференциальной функцией распределения» или «дифференциальным законом распределения» величины X.
|
|
|
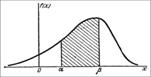
Кривая, изображающая плотность распределения случайной величины, называется кривой распределения.
Выразим вероятность попадания величины X на отрезок от α до β через плотность распределения:
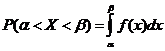
Основные свойства плотности распределения.
· Плотность распределения есть неотрицательная функция: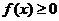 
· Интеграл в бесконечных пределах от плотности распределения равен единице: 
Дата добавления: 2018-05-13; просмотров: 201; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!