Применение центральной предельной теоремы.
а) Пусть  — независимые случайные величины с математическими ожиданиями
— независимые случайные величины с математическими ожиданиями 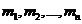 и дисперсиями
и дисперсиями 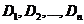
Предположим, что условия центральной предельной теоремы выполнены и число слагаемых п достаточно для того, чтобы закон распределения величины 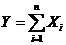 можно было считать приближенно нормальным.
можно было считать приближенно нормальным.
Тогда вероятность того, что случайная случайная величина У попадает в пределы участка 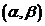 , выражается фопмулой
, выражается фопмулой
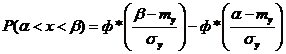
Где 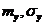 математическое ожидание и среднее квадратическое отклонение величины V,
математическое ожидание и среднее квадратическое отклонение величины V,
Ф* — нормальная функция распределения.
b) Частным случаем центральной предельной теоремы для дискретьых случайных величин является теорема Лапласа.
Если производится п независимых опытов, в каждом из которых событие А появляется с вероятностью р, то справедливо соотношение
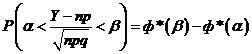
где Y — число появлений события А в n опытах, q = l — р.
Задача 15.7
Экзаменационный Билет №27
Закон Пуассона.
Дискретная случайная величина X называется распределенной по закону Пуассона, если ее возможные значения 0,1,2,..., m, ..., а вероятность того, что X = m, выражается формулой
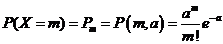
где а > 0 — параметр закона Пуассона.
Математическое ожидание и дисперсия случайной величины X, распределенной по закону Пуассона, равны параметру закона а: mx = а = Dx .
для вычисления вероятности Рm, n того, что событие А появится ровно m раз, можно воспользоваться приближенной формулой
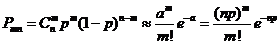
О парной и групповой зависимости случайных событий.
|
|
|
Несколько событий называют попарно независимыми, если каждые два из них независимы. Например, события А, В, С попарно независимы, если независимы события А и В, А и С, В и С.
События 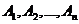 называются независимыми в совокупности, если для любого
называются независимыми в совокупности, если для любого 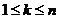 и любого набора различных меж собой индексов
и любого набора различных меж собой индексов 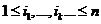 имеет место равенство:
имеет место равенство:
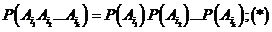
Если события 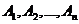 независимы в совокупности, то они попарно независимы, т.е. любые два события
независимы в совокупности, то они попарно независимы, т.е. любые два события 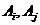 независимы. Достаточно в равенстве
независимы. Достаточно в равенстве 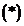 взять
взять 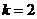
Подчеркнем, что если несколько событий независимы попарно, то отсюда еще не следует их независимость в совокупности. В этом смысле требование независимости событий в совокупности сильнее требования их попарной независимости.
Задача 31.10
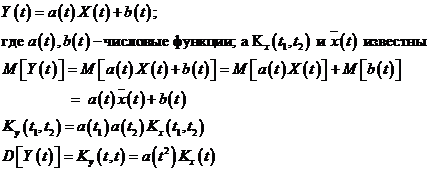
Экзаменационный Билет №28
Числовые характеристики случайных функций.
Рассмотрим сечение случайной функции X (t) при фиксированном t.
Математическим ожиданием случайной функции X(t) называется неслучайная функция mx(t), которая при каждом значении аргумента t равна математическому ожиданию соответствующего сечения случайной функции.
mx(t) = M{X(t)}
Дисперсией случайной функции X (t) называется неслучайная функция Dx(t), значение которой для каждого t равно дисперсии соответствующего сечения случайной функции:
|
|
|
Dx(t) = D{X(t)}
Среднее квадратическое отклонение случайной функции:
σx(t) = 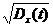
Корреляционная функция характеризует степень зависимости между сечениями случайной функции, относящимися к различным t.
Корреляционной функцией случайной функции X(t) называется неслучайная функция двух аргументов Kx(t, t’), которая при каждой паре значений t, t’ равна корреляционному моменту соответствующих сечений случайной функции:
Ky(t, t’) = M[ 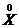 (t)
(t) 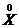 (t’)]
(t’)]
Где, 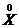 (t) = X(t) – mx(t);
(t) = X(t) – mx(t); 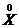 (t’) = X(t’) – mx(t’);
(t’) = X(t’) – mx(t’);
Пологая t = t’ è Ky(t, t’) = M[( 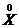 (t))2] = Dx(t)
(t))2] = Dx(t)
Ky(t, t’) = Ky(t’, t)
Вместо корреляционной функции Kx(t, t') можно пользоваться нормированной корреляционной функцией: 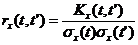
При t'=t нормированная корреляционная функция равна единице:
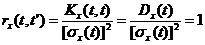
Неслучайная функция p(t):
· Y(t) = X(t) + p(t) è my(t) = mx(t) + p(t); Ky(t, t’) = Kx(t, t’)
· Y(t) = p(t)X(t) è my(t) =mx(t)*p(t); Ky(t, t’) = p(t)p(t’)Kx(t, t’)
Нормированной называется случайная функция вида: 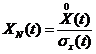
Корреляционная функция нормированной случайной функции XN(t) равна 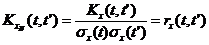
Дата добавления: 2018-05-13; просмотров: 379; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
