Порядок выявления аномальных значений
Аномальныеили“выскакивающие” значения - это единичные значения, сильно отличающиеся от основной массы. Выскакивающие значения могут появиться в случае ошибки при переписывании данных, при введении информации в компьютер, или, к примеру, если кто-то из испытуемых отнесся к исследованию психолога несерьезно и сообщил ложные данные, и еще во многих других случаях. “Выскакивающие” значения из дальнейших расчетов следует исключить.
Порядок проверки статистической гипотезы с помощью различных статистических критериев следующий:
1. Выборка упорядочивается в порядке возрастания вариант (то есть значений случайной величины).
2. Для проверки на аномальность (Ашмарин И.П. и др., 1971) наименьшего значения рассчитывается параметр
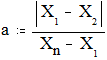
то есть частное от деления разности между наименьшей вариантой выборки и следующей за ней по величине |Х1- X2| на размах выборки (Xn-X1). Полученное эмпирическое значение сравнивается по абсолютной величине с критическим, приведенным в таблице 2 Приложения 1, для требуемого уровня достоверности. Если эмпирическое значение превышает критическое, либо равно ему по абсолютной величине, то наименьшую варианту следует признать аномальной и из дальнейших расчетов ее надо исключить.
3. Аналогично следует проверить на аномальность и наибольшую варианту. В этом случае рассчитывается частное от деления разности между наибольшей вариантой и предшествующей ей по величине (Хn- Xn-1) на размах выборки (Xn-X1):
|
|
|
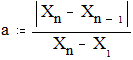
Полученное эмпирическое значение сравнивается с критическим (табл.2 Приложения 1). Если эмпирическое значение превышает критическое либо равно ему по модулю, то наибольшую варианту следует из дальнейших расчетов исключить как аномальную.
Например, имеется выборка, включающая следующие результаты испытуемых (данные упорядочены, то есть выписаны в порядке увеличения значений):
14, 19, 21, 23, 24, 25, 26, 27, 29, 31, 34, 36, 39, 54.
Проверка на наличие выскакивающих значений:
Минимальное значение: a = |14-19| = 5 = 0.125
54-14 40
Критическое значение а для 14 испытуемых равно 0.350 (р=0.05). Эмпирическое значение а меньше критического, следовательно, значение 14 аномальным не является.
Максимальное значение: a = |54-39| = 15 = 0.375
54-14 40
Эмпирическое значение 0.375 больше критического 0.350 (р=0.05), то есть значение 54 является аномальным, его следует из дальнейших расчетов исключить.
Все приведенные ниже в задачах данные проверены на наличие аномальных значений.
Проверка эмпирического распределения
На его соответствие нормальному распределению
|
|
|
Есть целый ряд методик, позволяющих проверить, значимо ли отличается исследуемое эмпирическое распределение от нормального. Эти методы описаны в специальной литературе по математической статистике. Представляется, что наиболее быстро и достаточно надежно можно сопоставить эмпирическое распределение с нормальным, выполнив следующие шаги:
1) построить полигон (или гистограмму) распределения и убедиться, что он напоминает колоколообразную кривую;
2) сравнить эмпирическое распределение с нормальным с помощью критерия c2 Пирсона по формуле
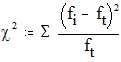
где fi - эмпирическая частота для интервала квантования, ft - теоретическая частота для того же интервала. Критерий Пирсона позволяет оценивать значимость отличия эмпирической частоты интервалов квантования от теоретической частоты для тех же интервалов.
Из свойств стандартного нормального распределения известно, какая часть испытуемых должна попадать в тот или иной интервал z-оценок в случае нормального распределения параметра. Можно подобрать граничные значения z, которые будут делить стандартное нормальное распределение на равные по количеству испытуемых части; удобно, если таких частей будет 5 или 4. Так, значения z,равные -0.85, -0.25, +0.25, +0.85 делят стандартное нормальное распределение на 5 частей по 20% испытуемых в каждой (N/5, где N - общее количество испытуемых) (таблица 1 Приложения). Величина N/5 представляет собой теоретическую (ожидаемую) частоту ft для интервалов квантования. Рассчитав z-оценки испытуемых исследуемой выборки, можно узнать, сколько испытуемых фактически имеют z-оценки от - ¥ до -0.85, сколько от -0.85 до -0.25, сколько от -0.25 до +0.25, сколько от +0.25 до +0.85 и сколько от +0.85 до +¥. Полученные 5 чисел представляют собой эмпирическую частоту fi для каждого из интервалов квантования. Зная fi и ft можно рассчитать эмпирическое значение параметра c2.
|
|
|
Порядок действий при сравнении эмпирического распределения с нормальным следующий:
1. Рассчитать среднее арифметическое Мх и стандартное отклонение s.
2. Рассчитать z-оценки испытуемых.
3. Подсчитать количество испытуемых, имеющих z-оценки от - ¥ до -0.85, от -0.85 до -0.25, от -0.25 до +0.25, от +0.25 до +0.85 и от +0.85 до +¥.
4. Рассчитать теоретическую частоту для интервалов квантования ft=N/5.
5. Сформулировать нулевую и альтернативную гипотезы:
Н0: Распределение случайной величины не отличается значимо от нормального.
Н1: Распределение случайной величины значимо отличается от нормального.
|
|
|
6. Рассчитать эмпирическое значение критерия c2 и сравнить его с критическим значением, взятым из таблицы с учетом числа степеней свободы n=k-3, где k - число интервалов квантования (в нашем случае k=5). При n=2 и доверительной вероятности 95% c2кр=5.99, при доверительной вероятности 90% c2кр=4.61, а при 1-a = 80% c2кр=3.22 (Таблица 3 Приложения). Поскольку при сравнении эмпирического распределения с нормальным исследователь заинтересован не допустить ошибку второго рода b, то для повышения надежности вывода следует принимать по возможности более низкий уровень доверительной вероятности. Если эмпирическое значение меньше критического, то принимается нулевая гипотеза: распределение признается не отличающимся значимо от нормального и для него можно использовать параметрические критерии.
Задача: Можно ли использовать для приведенной ниже выборки данных, характеризующих уровень социальной активности студентов в группе, состоящей из 26 человек, параметрические критерии?
14, 17, 26, 9, 21, 12, 17, 18, 11, 20, 18, 17, 25, 19, 15, 29, 16, 18, 24, 17, 16, 10, 11, 26, 14, 16.
Гистограмма для данной выборки имеет следующий вид (взяты интервалы [8-10], [11-13], [14-16], [17-19] и т.д.):
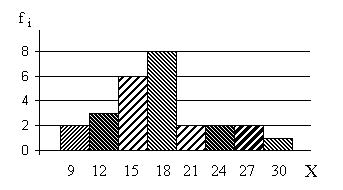
Рис. 7. Гистограмма распределения уровня социальной активности студентов.
Таблица 8.
Расчет z-оценок испытуемых
| Х | Х-Мх | (Х-Мх)2 | Z=(Х-Мх)/s | Х | Х-Мх | (Х-Мх)2 | Z=(Х-Мх)/s |
| 9 | -8,54 | 72,905 | -1,64 | 17 | -0,54 | 0,290 | -0,10 |
| 10 | -7,54 | 56,828 | -1,45 | 17 | -0,54 | 0,290 | -0,10 |
| 11 | -6,54 | 42,751 | -1,26 | 18 | 0,46 | 0,213 | 0,09 |
| 11 | -6,54 | 42,751 | -1,26 | 18 | 0,46 | 0,213 | 0,09 |
| 12 | -5,54 | 30,675 | -1,06 | 18 | 0,46 | 0,213 | 0,09 |
| 14 | -3,54 | 12,521 | -0,68 | 19 | 1,46 | 2,136 | 0,28 |
| 14 | -3,54 | 12,521 | -0,68 | 20 | 2,46 | 6,059 | 0,47 |
| 15 | -2,54 | 6,444 | -0,49 | 21 | 3,46 | 11,982 | 0,66 |
| 16 | -1,54 | 2,367 | -0,30 | 24 | 6,46 | 41,751 | 1,24 |
| 16 | -1,54 | 2,367 | -0,30 | 25 | 7,46 | 55,675 | 1,43 |
| 16 | -1,54 | 2,367 | -0,30 | 26 | 8,46 | 71,598 | 1,62 |
| 17 | -0,54 | 0,290 | -0,10 | 26 | 8,46 | 71,598 | 1,62 |
| 17 | -0,54 | 0,290 | -0,10 | 29 | 11,46 | 131,367 | 2,20 |
Среднее арифметическое значение выборки 17.54, дисперсия 27.138, стандартное отклонение 5.209. Расчет z-оценок приводится в таблице 8.
Сформулируем нулевую и альтернативную гипотезы:
Н0: Распределение случайной величины не отличается значимо от нормального.
Н1: Распределение случайной величины значимо отличается от нормального.
В интервале от -¥ до -0.85 фактически находится 5 стандартизированных значений, в интервал от -0.85 до -0.25 попадает 6 значений, интервал от -0.25 до +0.25 включает 7 значений, в интервале от +0.25 до +0.85 мы имеем 3 значения и, наконец, в интервал от +0.85 до + ¥ попадает 5 значений. Теоретическая частота для каждого интервала равна 26/5=5.2.
Значение c2эмп = (5-5.2)2+(6-5.2)2+(7-5.2)2+(3-5.2)2+(5-5.2)2 = 1.692
5.2
Критическое значение критерия c2 при a=0.20 составляет 3.22 (таблица 3 Приложения), эмпирическое значение 1.692 меньше критического, то есть мы можем принять нулевую гипотезу (a=0.20). Ответ задачи можно сформулировать следующим образом: “Использовать параметрические критерии для исследуемой выборки возможно, поскольку распределение случайной величины не отличается значимо от нормального (a=0.20)”.
Проверкой распределения на соответствие его нормальному типу, по-существу, заканчивается стадия подготовки данных. Результатом такой подготовки должна явиться таблица исходных данных, сопровождаемая параметрами распределения. Для распределений, близких к нормальному, внизу таблицы указываются среднее арифметическое, дисперсия и (или) стандартное отклонение.
Если распределение отличается значимо от нормального, то вместо среднего арифметического и стандартного отклонения следует указать медиану Ме и межквартильное отклонение q, которые более полно характеризуют центральную тенденцию и рассеивание таких распределений. Межквартильное отклонение q, рассчитывается по формуле

где Q1 и Q3 - соответственно первая и третья квартиль.
Далее, в зависимости от характера поставленной задачи, объема выборок, типа выборок (зависимые или независимые) и свойств распределений (нормальное или отличное от него) выбирается критерий для ее решения. Параметрические критерии следует использовать только при достаточном объеме (более 15-20 испытуемых) и нормальном распределении обоих выборок. Во всех остальных случаях лучше использовать непараметрические методы. Основные виды задач и рекомендуемые методы их решения приведены в таблице 9.
Таблица 9.
Дата добавления: 2018-05-12; просмотров: 4295; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
