Технология вычисления интегралов в среде математических пакетов
Способ вычисления определенного интеграла с использованием системы Mathcad впрямую зависит от способа задания подынтегральной функции. Если подынтегральная функция задана в аналитическом виде, то интеграл, так же как и производные, может быть вычислен с использованием встроенного в систему оператора, шаблон которого также расположен на палитре Исчисления. При этом выражение для подынтегральной функции может быть или предварительно описано в виде функции, или непосредственно введено в формат интеграла.
Пример 6.4.6-1. Найти определенный интеграл в символьном виде и вычислить его значение.
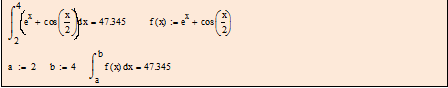
|
Однако нередко возникает необходимость вычисления определенного интеграла для таблично заданной функции. Тогда прямое применение встроенного в систему оператора вычисления интеграла оказывается невозможным.
Пример 6.4.6-2. Вычислить определенные интегралы методами трапеций (It) и парабол (Симпсона) (Ic).
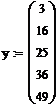 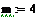 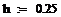 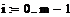 Метод трапеций
Метод трапеций 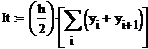 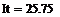 Метод Симпсона
Метод Симпсона 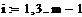 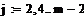
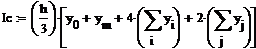 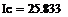
|
Пример 6.4.6-3. Вычислить значения определенного интеграла методом средних прямоугольников при условии, что подынтегральная функция задана аналитически.
Метод средних прямоугольников
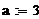 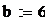 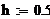 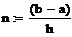 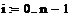
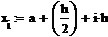 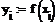
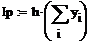 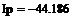
|
С помощью средств Mathcad могут быть найдены символьные выражения для производных и интегралов. Символьный знак равенства (стрелка) расположен на палитре Символика панели Математика. Для получения производных и интегралов в символьных выражениях в шаблон производной или интеграла нужно ввести выражение, щелкнуть по изображению символьного знака равенства, а затем щелкнуть по свободному пространству рабочего поля экрана.
|
|
|
Пример 6.4.6-4. Вычислить значения определенного интеграла с шагом 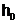 и
и 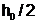 (
( 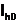 и
и  ) по формуле средних прямоугольников и оценить погрешность.
) по формуле средних прямоугольников и оценить погрешность.
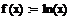 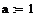  i:=0…n-1 i:=0…n-1
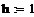 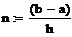 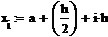 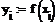 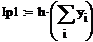 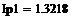
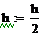 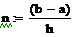 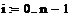 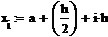 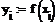 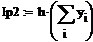 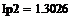
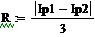 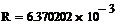
|
Пример 6.4.6-5. Вычислить значения определенного интеграла с шагом 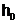 и
и 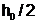 (
( 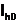 и
и  ) по формуле трапеций.
) по формуле трапеций.
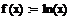 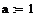 
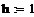 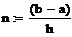 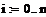 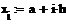
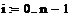 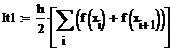 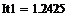
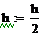 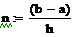 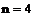 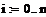 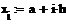
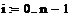 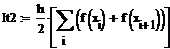 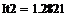
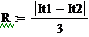 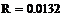
|
Пример 6.4.6-6. Вычислить значения определенного интеграла с шагом  и
и 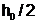 (
( 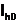 и
и  ) по формуле Симпсона.
) по формуле Симпсона.
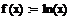   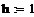 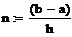 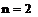
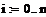 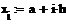 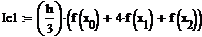 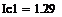
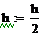 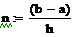 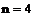 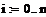 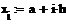
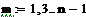 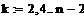 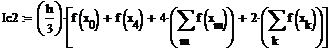 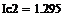
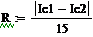 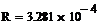
|
Тема 6.5. Методы решения обыкновенных дифференциальных уравнений
Постановка задачи
Метод Эйлера
Методы Рунге-Кутты
Решение ОДУ n-го порядка
Сравнение методов решения ОДУ
Технология решения ОДУ средствами математических пакетов
Постановка задачи
Любое физическое явление, в котором рассматривается степень изменения одной переменной по отношению к другой переменной, математически описывается дифференциальным уравнением (ДУ). Из курса высшей математики известно множество аналитических методов, позволяющих найти их решения. Однако, в некоторых случаях, например, если функция или коэффициенты ДУ представляют собой таблицу экспериментально полученных данных, использование аналитических методов невозможно.
|
|
|
Рассмотрим ряд численных методов, позволяющих без проведения сложных математических вычислений найти с заданной точностью решения обыкновенных дифференциальных уравнений (ОДУ).
Из курса математического анализа известно, что обыкновеннымназывается такое дифференциальное уравнение от одной переменной, которое содержит одну или несколько производных от искомой функции y(x). В общем виде ОДУ можно представить следующим образом:
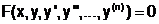 (6.5.1-1)
(6.5.1-1)
где х – независимая переменная, а n – порядок ОДУ.
Численные методы позволяют решить только ОДУ 1-го порядка, поэтому в дальнейшем будем рассматривать только такие уравнения. Следует отметить, что ОДУ n-го порядка можно привести к системе из n уравнений 1-го порядка, и при решении системы применить те же методы.
Известно, что для ОДУ 1-го порядка справедливы следующие формы записи:
|
|
|
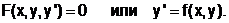
Вторая форма записи называется ОДУ, разрешенным относительно старшей производной.
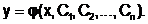 |
Решением ОДУ первого порядка называется такая функция, которая при подстановке в уравнение обращает его в тождество. При этом различают общее и частное решения ОДУ.
Общее решение ОДУ содержит n произвольных постоянных С1, С2, . . .,Сn и имеет следующий вид:
Общее решение ОДУ первого порядка содержит одну произвольную постоянную
y = j(x,C) и описывает множество функций, удовлетворяющих уравнению y¢ = f(x,y)
(рис. 6.5.1-1).
Если произвольная постоянная принимает конкретное значение С=С0, то из общего решения ОДУ, в соответствии с теоремой Коши, получаем частное решение y = j(x,C0), поскольку через каждую точку (x0, y0) в области допустимых значений проходит только одна интегральная кривая.
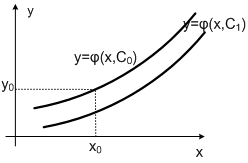
Рис. 6.5.1-1
Теорема Коши для ОДУ 1-го порядка звучит так:
Если в ОДУ функция y¢ = f(x,y) и ее частная производная f¢ (x,y) определены и непрерывны в некоторой области G изменения переменных x и y, то для всякой внутренней точки (x0, y0) этой области данное уравнение имеет единственное решение.
Значения x0, y0 называются начальными условиями. Для ОДУ 2-го порядка, общее решение которого имеет две произвольные постоянные, в качестве начальных значений выступают x0, y0 = j(x0) и y0¢=φ¢ (x0).
|
|
|
При решении ОДУ точным решением является аналитическое выражение функции
y = j(x), а результатом решения ОДУ численными методами является таблица значений
y = j(x) на некотором множестве значений аргумента х. Поэтому при постановке задачи численного решения ОДУ наряду с начальными условиями x0, y0 необходимо задать область решения - отрезок [a;b] и шаг изменения аргумента h.
Таким образом, численное решение ОДУ представляет собой таблицу значений искомой функции для заданной последовательности аргументов, xi+1=xi+h, i=0, 1, …,n, где h = xi+1-xi называется шагом интегрирования.
Выделяют два класса методов решения ОДУ: одношаговые и многошаговые. В одношаговых методах для нахождения следующего значения функции требуется значение только одной текущей точки, то есть
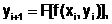
а в многошаговых – нескольких, например
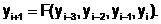
Начинать решение задачи Коши многошаговыми методами нельзя, поэтому начинают решение, используя всегда одношаговые методы.
Основная идея решения ОДУ одношаговыми методами сводится к разложению искомого решения y(x) в ряд Тейлора в окрестности текущей точки и его усечению. Число оставшихся членов ряда определяет порядок и, следовательно, точность метода.
Рассмотрим наиболее распространенные одношаговые численные методы решения ОДУ.
Метод Эйлера
Пусть дано уравнение
y¢=f(x,y), (6.5.2-1)
с начальными условиями x0, y0 = y(x0). Требуется найти решение данного уравнения на отрезке [a;b] (обычно x0=а) в n точках.
На рис. 6.5.2-1 график искомой функции y(x) проходит через точку А(x0,y0), заданную начальными условиями.
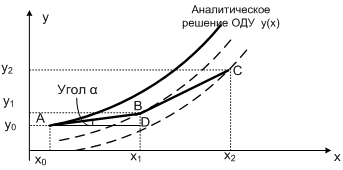
Рис. 6.5.2-1
Разобьем отрезок на n равных частей и получим последовательность x0,x1,…, xn, где xi=x0+i∙h (i=0, 1, …,n), а h = (b-a)/n – шаг интегрирования.
Найдем yi = y(xi). Для этого проинтегрируем производную, заданную (6.5.2-1) на интервале [x0;x1], по формуле Ньютона – Лейбница:
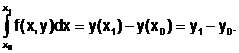
Отсюда значение искомой функции в точке x1
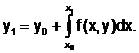
Примем допущение, что на интервале [x0;x1]производная исходной функции постоянна и равна своему значению в точке А(x0,y0). Тогда по формуле прямоугольников
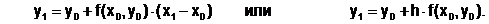
Полученное выражение имеет наглядную геометрическую интерпретацию (рис. 6.5.2-1) . Поскольку значение производной f’(x0,y0) = tga, то в прямоугольном треугольнике ABD Dy0=h×tga, и, следовательно, y1 = y0+Dy0 = y0+h×f¢(x0,y0). Таким образом, y1 может быть найдено геометрически в результате замены искомой кривой y(x) касательной, проведенной в точке А.
Продолжая этот процесс и принимая подынтегральную функцию f(x) на соответствующем участке [xi,xi+1] постоянной и равной ее значению в начале отрезка, получим решение дифференциального уравнения в виде значений искомой функции y(x) на отрезке [a;b]. График решения представляет собой ломаную линию, которая называется ломаной Эйлера. При этом общая формула для определения очередного значения функции имеет вид:
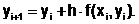 (6.5.2-2)
(6.5.2-2)
Метод Эйлера является сравнительно грубым и применяется на практике в основном для проведения ориентировочных расчетов.
Погрешность метода Эйлера связана с величиной шага интегрирования отношением e1 =C1h2, где C1 – произвольная постоянная.
Пример 6.5.2-1. Решить методом Эйлера ОДУ y¢= 2x/y с начальными условиями x0 = 1 и y0 = 1 на отрезке [1;1.4] с шагом h = 0.2.
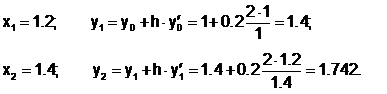
|
Методы Рунге-Кутты
Методы Рунге-Кутты – это группа методов, широко применяемых на практике для решения ОДУ. В этих методах при вычислении значения искомой функции в очередной точке хi+1 используется информация о предыдущей точке хi, yi. Методы различаются объемом вычислений и точностью результата.
Порядок метода Рунге-Кутты определяется кратностью вычисления значения производной искомой функции f(x,y)на каждом шаге. В соответствии с этим метод Эйлера является методом Рунге-Кутты первого порядка, поскольку для получения очередного значения yi+1 функция f(x) вычисляется один раз в предыдущей точке хi, yi. В методах Рунге-Кутты более высоких порядков для вычисления очередного значения искомой функции в точке хi+1 значение правой части уравнения y’= f(x,y) вычисляется несколько раз, количество которых и определяет порядок метода.
Метод Рунге-Кутты 2-го порядка (Усовершенствованный метод Эйлера). Вычисление значения искомой функции в точке хi+1 проводится в два этапа. Сначала вычисляют вспомогательную величину 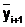 по методу Эйлера:
по методу Эйлера:
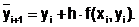 (6.5.3-1)
(6.5.3-1)
Затем значение производной искомой функции в точке (xi+1,yi+1) используется для вычисления окончательного значения функции:
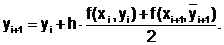 (6.5.3-2)
(6.5.3-2)
Подставляя (6.5.3-1) в (6.5.3-2), окончательно получим расчетную формулу метода Рунге-Кутты 2-го порядка:
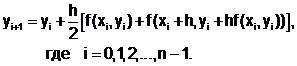 (6.5.3-3)
(6.5.3-3)
Этот метод также называют методом прогноза и коррекций. Сначала находят грубое приближение 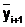 по методу Эйлера (прогноз), а затем уточненное значение yi+1 (коррекция).
по методу Эйлера (прогноз), а затем уточненное значение yi+1 (коррекция).
В общем виде формулу (6.5.3-3) можно представить как
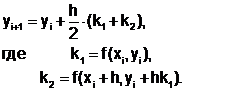 (6.5.3-4)
(6.5.3-4)
Метод Рунге-Кутты второго порядка имеет наглядную геометрическую интерпретацию (рис. 6.5.3-1). Построение проводится следующим образом: 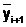 определяется пересечением перпендикуляра, восстановленного из точки xi+1 c касательной L1, проведенной к кривой y(x) в предыдущей точке (хi,yi). Затем в точке
определяется пересечением перпендикуляра, восстановленного из точки xi+1 c касательной L1, проведенной к кривой y(x) в предыдущей точке (хi,yi). Затем в точке 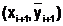 проводится прямая L2 с тангенсом угла наклона, равным
проводится прямая L2 с тангенсом угла наклона, равным 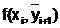 . Прямую
. Прямую 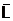 проводят через точку
проводят через точку 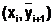 под углом, тангенс которого находим усреднением значений тангенсов углов наклона L1 и L2. Прямая L проводится параллельно
под углом, тангенс которого находим усреднением значений тангенсов углов наклона L1 и L2. Прямая L проводится параллельно 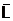 через точку (хi,yi). Ее пересечение с перпендикуляром, восстановленным из точки хi+1, и дает уточненное значение yi+1.
через точку (хi,yi). Ее пересечение с перпендикуляром, восстановленным из точки хi+1, и дает уточненное значение yi+1.
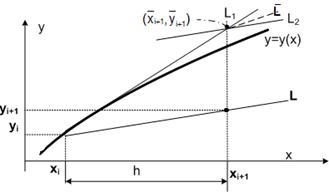
Рис. 6.5.3-1
Погрешность метода Рунге-Кутты второго порядка связана с величиной шага интегрирования отношением e2 =C2h3, где C2– произвольная постоянная.
Пример 6.5.3-1. Решить методом Рунге-Кутты второго порядка ОДУ y¢= 2x/y с начальными условиями x0 = 1 и y0 = 1 на отрезке [1;1.4] и шагом h = 0.2.
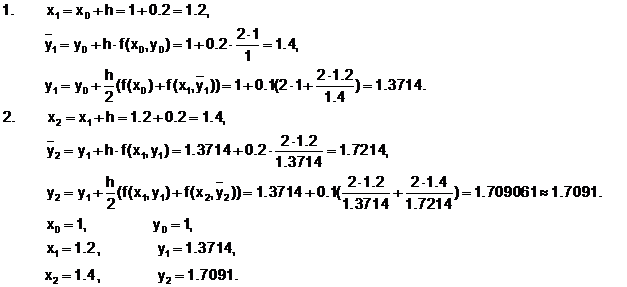 Проводя дальнейшее обобщение формул Рунге-Кутты, для решения ОДУ первого порядка можно записать следующее:
Проводя дальнейшее обобщение формул Рунге-Кутты, для решения ОДУ первого порядка можно записать следующее:
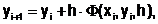
где Ф – линейная функция аргументов x, y, h и f(x,y), которая может быть представлена как
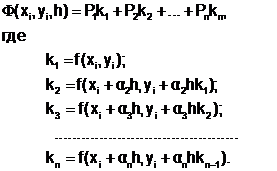 (6.5.3-5)
(6.5.3-5)
Величина n в (6.5.3-4) определяется порядком метода, а коэффициентам a2,a3, … ,an, Р1, Р2, … ,Pn подбирают такие значения, которые обеспечивают минимальную погрешность. Так, для метода Рунге-Кутты четвертого порядка (n=4) получена расчетная формула при следующих коэффициентах: a2= a3=1/2, a4=1, P1 = P4=1/6, P2 = P3 =2/6.
Подставив значения коэффициентов в (6.5.3-4), имеем
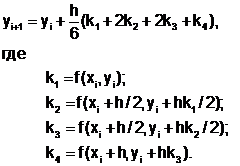 (6.5.3-6)
(6.5.3-6)
Геометрическая интерпретация этого метода очень сложна и потому не приводится.
Погрешность метода Рунге-Кутты четвертого порядка значительно меньше методов первого и второго порядков и пропорциональна величине h (e4 =C4h5).
Пример 6.5.3-2. Решить методом Рунге-Кутты четвертого порядка ОДУ y¢= 2x/y с начальными условиями x0 = 1 и y0 = 1 на отрезке [1;1.4] с шагом h = 0,2.
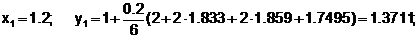
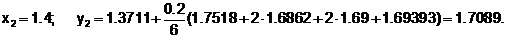
|
Сведем в таблицу результаты решения уравнения y¢=2x/y методами Рунге-Кутты, соответственно, первого (y1i), второго (y2i) и четвертого (y4i) порядков и сравним с результатами, полученными точным методом (yi).
| хi | y1i | y2i | y4i | yi |
| 1 1.2 1.4 | 1 1.4 1.74286 | 1 1.3714 1.7091 | 1 1.37115 1.7089 | 1 1.37113 1.7088 |
На практике для обеспечения требуемой точности (при использовании любого приближенного метода решения ОДУ) применяется автоматический выбор шага методом двойного просчета. При этом в каждой точке хi по формуле, соответствующей выбранному методу, производится расчет yi с шагом h (yi(h)) и с шагом h/2 (yi(h/2)). Цель двойного просчета состоит в том, чтобы для каждой точки численного решения эти значения отличались на величину, не превышающую заданной погрешности e. В этом случае общая формула для оценки погрешности решения ОДУ методами Рунге-Кутты имеет следующий вид:
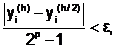
где p – порядок метода Рунге-Кутты. Эта формула называется также правилом Рунге.
Если | yi(h)) - yi(h/2)|< e, то шаг для следующей точки выбирается равным h, иначе шаг уменьшается вдвое и продолжается уточнение y i в точке хi.
Решение ОДУ n-го порядка
Методы, рассмотренные выше, позволяют найти численное решение ОДУ только первого порядка. Однако они применимы и к уравнениям n-го порядка. Для этого ОДУ n-го порядка предварительно приводится к системе n уравнений первого порядка.
Пусть, например, требуется решить ОДУвторого порядка
 ,
,
с начальными условиями 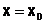 ,
, 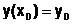 ,
, 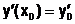 .
.
Обозначим  z=y’. В результате подстановки в исходное уравнение получим систему двух уравнений первого порядка
z=y’. В результате подстановки в исходное уравнение получим систему двух уравнений первого порядка
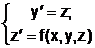 ,
,
с двумя неизвестными функциями 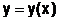 и
и 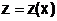 и начальными условиями
и начальными условиями
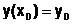 ,
, 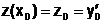 .
.
В общем виде система уравнений может быть представлена в виде
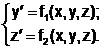 (6.5.4-1)
(6.5.4-1)
Решением системы (6.5.4-1) являются две функции 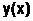 и
и 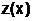 , из которых
, из которых 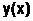 - решение исходного уравнения второго порядка. Выбрав, например, метод Эйлера, приближенное решение системы (6.5.4-1) можно найти с помощью двух рекуррентных формул:
- решение исходного уравнения второго порядка. Выбрав, например, метод Эйлера, приближенное решение системы (6.5.4-1) можно найти с помощью двух рекуррентных формул:
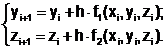
Пример 6.5.4-1. Дано обыкновенное дифференциальное уравнение второго порядка 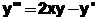 при начальных условиях
при начальных условиях 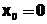 ,
, 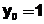 ,
, 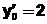 на отрезке [0;0.4] с шагом
на отрезке [0;0.4] с шагом 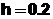 .
.
Обозначим 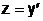 , тогда ОДУ второго порядка можно записать в виде системы ОДУ первого порядка
, тогда ОДУ второго порядка можно записать в виде системы ОДУ первого порядка
 с начальными условиями
с начальными условиями 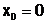 ,
, 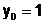 ,
,  .
.
Применим метод Эйлера для решения системы ОДУ
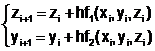
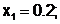
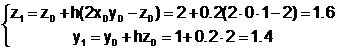
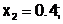
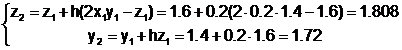 и т.д.
и т.д.
| xi | yi | zi |
| 0 | 1 | 2 |
| 0.2 | 1.4 | 1.6 |
| 0.4 | 1.72 | 1.808 |
В общем виде ОДУn-го порядка
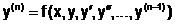 .
.
Введем следующие обозначения:
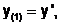
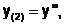 …
… 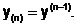
В результате этих подстановок перейдем к системе n ОДУ первого порядка:
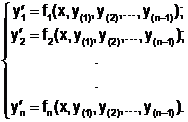 (6.5.4-2)
(6.5.4-2)
Решением системы (6.5.4-2) являются функции 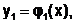
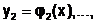
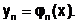
При заданных начальных условиях 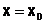 ,
, 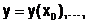
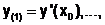
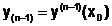 и использовании метода Эйлера решение может быть получено с помощью рекуррентных формул
и использовании метода Эйлера решение может быть получено с помощью рекуррентных формул
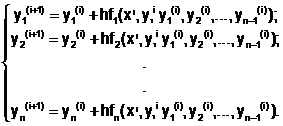
Окончательным решением ОДУ n-го порядка, согласно определению, служит функция 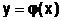 , вычисленная на заданном множестве точек [a;b].
, вычисленная на заданном множестве точек [a;b].
Дата добавления: 2018-05-12; просмотров: 468; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
