Уравнение прямой для этого случая имеет вид
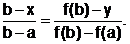
Очередное приближение х1 при y = 0
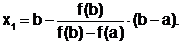
Тогда рекуррентная формула метода хорд для этого случая имеет вид
 (6.2.3-14)
(6.2.3-14)
Следует отметить, что за неподвижную точку в методе хорд выбирают тот конец отрезка [a;b], для которого выполняется условие f (x)∙ f¢¢ (x)>0.
Таким образом, если за неподвижную точку приняли точку а,то в качестве начального приближения выступает х0 = b, и наоборот.
Достаточные условия, которые обеспечивают вычисление корня уравнения f(x)=0 по формуле хорд, будут теми же, что и для метода касательных (метод Ньютона), только вместо начального приближения выбирается неподвижная точка. Метод хорд является модификацией метода Ньютона. Разница состоит в том, что в качестве очередного приближения в методе Ньютона выступает точка пересечения касательной с осью 0Х, а в методе хорд – точка пересечения хорды с осью 0Х – приближения сходятся к корню с разных сторон.
Оценка погрешности метода хорд определяется выражением
 (6.2.3-15)
(6.2.3-15)
Условие окончания процесса итераций по методу хорд
 (6.2.3-16)
(6.2.3-16)
В случае, если M1<2m1, то для оценки погрешности метода может быть использована формула | xn - xn-1| £ e.
Пример 6.2.3-4. Уточнить корень уравнения ex – 3x = 0, отделенный на отрезке [0;1] с точностью 10-4.
Проверим условие сходимости:
|
|
|

Следовательно, за неподвижную точку следует выбрать а=0, а в качестве начального приближения принять х0=1, поскольку f(0)=1>0 и f(0)*f"(0)>0.
Результаты расчета, полученные с использованием формулы
6.2.3-14, представлены в таблице 6.2.3-4.
Таблица 6.2.3-4
| i | x | f(x) |
| 1 | 0.7812 | -0.1569 |
| 2 | 0.6733 | -0.0591 |
| 3 | 0.6356 | -0.0182 |
| … | ……….. | ……….. |
| 8 | 0.6191 | -4.147∙10-5 |
Требуемая точность достигается на 8-й итерации. Следовательно, за приближенное значение корня можно принять х = 0.6191.
Сравнение методов решения нелинейных уравнений
Метод половинного деления очень прост и имеет одно явное преимущество по сравнению со всеми рассмотренными выше методами – он всегда сходится. Однако, скорость сходимости очень мала, поэтому его часто используют для грубого уточнения корня.
Метод касательных (метод Ньютона) эффективен для решения уравнений, график которых в окрестности корня имеет большую крутизну. Метод обладает высокой скоростью сходимости, но его сходимость зависит от вида функции, поэтому рекомендуется отрезок, на котором отделяется корень, выбирать очень небольшой длины.
Метод хорд, являясь модификацией метода касательных, также обладает хорошей скоростью сходимости. При правильном выборе неподвижной точки последовательность приближений гарантированно сходится к корню уравнения.
|
|
|
Метод простой итерации дает возможность «угадывать» новые значения х на любом шаге. Следовательно, если процесс сходится медленно, можно вносить коррективы, учитывая предыдущие результаты. Метод прост и обладает хорошей сходимостью. Однако перед его использованием требуется преобразование исходного уравнения и проведение дополнительных вычислений.
Отметим, что на практике при решении нелинейных уравнений обычно используется комбинация нескольких методов.
Дата добавления: 2018-05-12; просмотров: 210; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
