Проекция силы на ось и на плоскость
Скалярная величина, равная взятой с соответствующим знаком длине отрезка, заключенного между проекциями начала и конца силы называется проекцией силы на ось.
Знак плюс проекция имеет, если перемещение от начала к концу происходит в положительном направлении оси, и знак минус если в отрицательном.
Таким образом, проекции данной силы на любые параллельные и одинаково направленные оси равны друг другу.
Проекция силы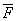 
на ось Ох обозначается как 
.
Следуя рисунку 12 и определению получаем
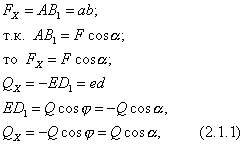
To есть проекция силы на ось равна произведению модуля силы на косинус угла между направлением силы и положительным направлением оси.
Если сила перпендикулярна оси, то ее проекция на эту ось равна нулю.
Проекцией силы 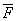на плоскость Оху называется вектор 
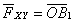, заключенный между проекциями начала и конца силы F на эту плоскость .
Проекция силы на плоскость есть величина векторная и характеризуется как модулем, так и направлением в плоскости Оху. Модуль проекции силы 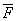на плоскость Оху выражается как
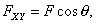
Тогда проекции на оси Ох и Оу:
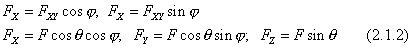
Вопрос 5(Геометрический и аналитический способы сложения сил.)
Аналитически способ задания и сложения сил
Выберем систему координат Oxyz. Вектор 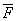можно построить, зная модуль 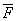и углы 
между вектором и соответствующими осями .
Задание этих величин и определяет силу 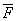. Точка приложения силы должна быть задана дополнительно координатами х, у, z. Кроме того, силу можно задавать проекциями на оси 
. Тогда
|
|
|
Эти формулы позволяют, зная проекции силы на оси координат найти ее модуль и углы с осями, т.е. определить силу. Зная проекции, можно построить вектор геометрически.
Для плоскости формулы (2.2.1) и (2.2.2) запишутся
Построение в плоскости производится по 4-й аксиоме статики.
Рассмотрим теперь аналитический способ сложения сил. Зависимость между векторами и их проекциями дает следующая теорема:
Проекция вектора суммы на какую-нибудь ось равна алгебраической сумме проекций слагаемых векторов на ту же ось .
Данные соотношения позволяют складывать силы аналитически. Можно заметить идентичность формул (2.2.1)-(2.2.4) и (2.2.9)-(2.2.11).
Геометрический способ сложения сил
Решение задач в статике часто связано с операцией сложения из векторной алгебры. Вспомним старые приемы и введем некоторые определения.
Величина, равная геометрической сумме сил какой-либо системы, называется главным вектором системы.
Геометрическую сумму сил не следует смешивать с равнодействующей. Для многих систем сил равнодействующей не существует, а главный вектор можно вычислить для любой.
Рассмотрим сложение двух сил на плоскости. Геометрическая сумма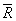 
сил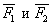 
находится по правилу параллелограмма построением силового треугольника .
|
|
|
Модуль R равнодействующей определяем как сторону 
треугольника 
:
углы 
находим по теореме синусов, учитывая, что 
, получаем
В продолжение геометрического способа сложения сил, напомним о сложении трех сил не лежащих в оной плоскости.
Геометрическая сумма 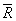трех сил 
, не лежащих в одной плоскости изображается диагональю параллелепипеда, построенного на этих силах .
Здесь необходимо подчеркнуть полную аналогию рисунков 14 и 17, где в роли 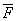выступает 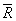, а в роли 
соответственно . Coответственно мы можем использовать формулы (2.2.1-2.2.4).
Рассматривая плоскую систему сходящихся сил необходимо рассмотреть и положение такой системы сил.
Геометрическая сумма (главный вектор) любой системы сил определяется построением силового многоугольника или последовательным сложением сил системы. Пусть дана система 
сходящихся сил .
Для построения силового многоугольника выбираем произвольную точку О и переносим в нее начало 
, затем переносим в конец вектора начало 
и т.д. после переноса вектора 
конец вектора будет в некоторой точке N. Соединяем точки О и N вектором 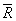. Этот замыкающий вектор и будет главным вектором системы.
|
|
|
При последовательном сложении сил (рис. 18, а) все они переносятся вдоль линий действия в точку пересечения А. Последовательно, по правилу параллелограмма, складываются силы 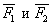получается вектор 
:
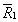который представляет собой равнодействующую, равную главному вектору всех сил и приложенную в точке их пересечения.
Дата добавления: 2018-05-12; просмотров: 709; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!